水封洞库裂隙岩体渗流力学特性研究

Study on the Mechanical Characteristics of Seepage in Fractured Rock Mass of Water Sealed Cave Reservoir

摘要: 天然岩体由于裂隙的存在，渗透性具有明显的各向异性，研究裂隙岩体的渗透特性对准确刻画库区渗流场特征、保证洞室水封性具有重要意义。以宁波某地下水封洞库主洞室裂隙岩体裂隙特征统计数据为基础，分析得到优势裂隙组各项特征，应用Monte-Carlo随机模拟技术生成二维离散裂隙网络(DFN)模型，并计算得到不同尺寸试样的等效渗透系数。结果表明：试样尺寸达到110 m × 110 m后，试样可等同于连续介质，此时的试样为裂隙岩体渗流表征单元体(REV)。

Abstract: Due to the presence of fractures, natural rock masses exhibit significant anisotropy in permeability. Studying the permeability characteristics of fractured rock masses is of great significance for accurately characterizing the characteristics of the seepage field in the reservoir area and ensuring the water sealing of caverns. Based on the statistical data of rock fracture characteristics in the main chamber of a groundwater sealed reservoir in Ningbo, various characteristics of dominant fracture groups were analyzed. Monte-Carlo random simulation technology was applied to generate a two-dimensional discrete fracture network (DFN) model, and the equivalent permeability coefficients of samples of different sizes were calculated. The results show that when the sample size reaches 110 m × 110 m, the sample can be equated to the continuous medium, and the sample is the fractured rock seepage characterization unit (REV).

1. 引言

自然界岩体中充斥着大量的不连续面，使岩体渗透性呈现非均质性和各向异性，具有明显的尺寸效应，岩体渗透性随着研究尺寸大小变化而变化，当研究尺寸达到某一值时，渗透参数趋于稳定，这个值所对应的尺寸即为该裂隙岩体的渗透REV [1] [2] 。高超等 [3] 基于COMSOL数值模拟软件对岩体单裂隙尺寸效应进行研究，表明单裂隙岩体的渗透性随试样尺寸增大而增大，随后趋于一稳定值。刘日成等 [4] 通过改变流体方向，得到不同流动方向下裂隙岩体的等效渗透系数，结果表明表征单元体存在的条件是等效渗透系数保持稳定并渗透椭圆比较光滑。张贵科 [5] 利用岩体裂隙网络模拟程序得出了岩体REV尺度约为各组裂隙中最大迹长期望值的3~4倍。

2. 工程概况

研究区地下水封洞库工程位于浙江省宁波市大榭岛内，根据地质时代、成因、岩性及工程性质的不同，工程建设场地内的地层岩性可分为4大类：① 第四系人工填土层、冲洪积层、残坡积层(Q^ml、Q^el+dl、Q^al+pl)；② 上侏罗统高坞组(J3g)花岗斑岩；③ 西山头组(J3x)含角砾熔结凝灰岩；④ 上侏罗统煌斑岩、安山岩和辉绿岩等各种岩脉。拟建洞库虽未穿过主要断裂，但覆盖岩体节理裂隙稍发育，局部存在节理裂隙密集带。

3. 主洞室岩体裂隙发育情况

洞库主洞室层处于中等应力区，应力条件较好，在地质素描过程中，未见高应力区及岩爆等不利情况。角砾熔结凝灰岩和花岗斑岩是拟建洞库的主要覆盖岩体，局部发育煌斑岩，在凝灰岩与花岗斑岩交界处，岩体较破碎，节理较发育(如图1)。开挖的7条主洞室普遍发育三组节理，节理倾角大多较陡，整体较密集，节理面平直且闭合度较高(如图2)。东部局部地段巷道围岩主要为微风化含角砾熔结凝灰岩，中西部巷道围岩主要为微风化花岗斑岩。场地内未见断层分布，受区域构造影响不间断夹节理裂隙密集带和绿泥石化蚀变现象，岩体透水性较弱，地下水水量受裂隙发育程度和连通性控制，总体不丰，局部水量大。

(a) 煌斑岩发育 (b) 岩性变化处 (c) 绿泥石蚀变

Figure 1. Excavation disclosure of main cavern

图1. 主洞室开挖揭露情况

(a) 交叉裂隙 (b) 近南北向裂隙 (c) 近东西向裂隙

Figure 2. The occurrence and development of fissure in main cavity

图2. 主洞室裂隙产状发育

3.1. 主洞室裂隙产状

主洞室裂隙产状常用倾向倾角表示，倾向倾角反映了裂隙在三维空间上的分布形态。裂隙常用的分布形式有均匀分布、Fisher分布、椭圆分布、Bingham分布、正态分布等。根据汪小刚 [6] 在水利工程应用的研究，将裂隙用倾角、倾向来单独模拟，可以简化研究复杂度，结果也较为合理。对7条主洞室，共计1140组裂隙倾向倾角数据进行统计，将倾向划分为15˚一组，倾角5˚一组，绘制优势裂隙面组J1、J2、J3频数分布直方图如图3所示。

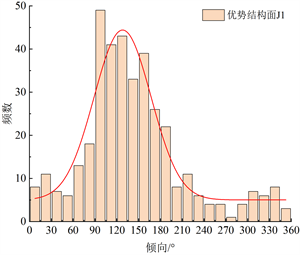
(a) J1倾向频数分布直方图 (b) J2倾向频数分布直方图

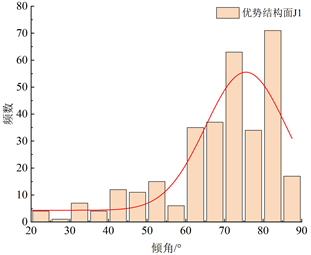
(c) J3倾向频数分布直方图(d) J1倾角频数分布直方图(e) J2倾角频数分布直方图 (f) J3倾角频数分布直方图

Figure 3. Main cavity fracture occurrence distribution histogram

图3. 主洞室裂隙产状分布直方图

Table 1. The fitting equation of fissure dip angle of main cavity and statistical table of parameters

表1. 主洞室裂隙倾角拟合方程及参数统计表

通过统计分析，主洞室裂隙J1、J2、J3倾向和J1、J2倾角基本符合正态分布(μ, $\delta$ )，其中µ为均值， $\delta$ 为标准差，三组优势裂隙倾向倾角正态分布参数如表1所示，裂隙组J3倾角拟合效果较差，本次研究取其倾角平均值53˚。裂隙产状分别为：128˚ $\angle$ 76˚ (J1)、112˚ $\angle$ 72˚ (J2)、307˚ $\angle$ 53˚ (J3)。

3.2. 主洞室裂隙密度

裂隙密度可分为一维裂隙密度、二维裂隙密度、三维裂隙密度，常用线密度、面密度、体密度来表征裂隙的密集程度，线密度指裂隙平均间距的倒数，面密度是指在某一裂隙露头面上，单位面积内平均裂隙条数，体密度是指单位体积内平均裂隙条数，但由于岩体的不透明性，很难测量，往往通过线密度或者面密度推算得知。对7条主洞室，共计1140组、9034条裂隙分布情况进行统计分析，根据地质素描所得数据，每条主洞室裂隙分布情况如表2所示。

Table 2. Statistical table of fracture distribution in main cavity

表2. 主洞室裂隙分布统计表

由表2主洞室裂隙分布统计可知，各个洞室J1线密度整体在0.7~0.9条/m，J2线密度整体在0.6~0.7条/m，J3线密度整体在0.4~0.6条/m。由于岩体质量受裂隙密度影响较大，此处仅考虑RQD值影响，得到裂隙面密度的分布范围，III2类岩体裂隙面密度为0.17~0.28条/m²，IV类岩体0.31~0.37条/m²，为后续便于计算，III2类岩体裂隙面密度取0.22条/m²，IV类岩体取0.34条/m²。根据3组裂隙线密度关系，不同等级岩体裂隙面密度如表3所示。

Table 3. Fracture density of rock mass of different grades in main cavern

表3. 主洞室不同等级岩体裂隙密度

3.3. 主洞室裂隙其他特征

1) 裂隙迹长

裂隙尺寸一般通过统计岩体外漏的迹长来表示，迹长是裂隙在揭露面显示的长度，由于其部分隐藏在岩体内部，出露迹线也并非裂隙面的准确尺寸，测量方法主要有测线统计法和统计窗法 [7] ，一般认为裂隙迹长服从对数分布或负指数分布 [8] [9] 。库区处于低山丘陵地貌带，山体均被茂密植被所覆盖，这对裂隙面地表迹长统计带来了极大的不便。通过对洞室层开挖揭露岩体进行统计分析得到裂隙迹长的分布特征，裂隙迹长处于10~15 m，符合正态分布。

2) 裂隙张开度

由于主洞室裂隙多发育为闭合裂隙，大多数裂隙开度在1 mm以下，利用现有技术手段难以测量裂隙开度，通常采用统计分布规律来表示，T. F. Wong [10] 等得出花岗岩和石英岩内节理隙宽幂律分布的指数分别为−1.843和−1.804；N. R. Barton [11] 等得出1~10 mm内隙宽幂律分布指数为1.53；W. C. Belfield [12] 得出6~40 um内隙宽幂律分布的指数为2.0~2.4。在本次研究中，假定隙宽满足幂率分布，取其分布指数为2，隙宽为0.1 mm。

3) 裂隙面位置

裂隙位置常用裂隙面中心点坐标来表示，目前广泛采用泊松分布 [13] ，根据泊松过程的假定，对于相同岩石质量等级的区域，裂隙中心点位置服从均匀分布。

3.4. 二维随机裂隙网络模型建立

基于前述主洞室裂隙特征，假设裂隙面均为平直光滑，不考虑填充物的影响，以III2类岩体为例，利用MATLAB编写程序，采用Monte-Carlo法生成二维随机裂隙网络模型如图4所示，裂隙位置由裂隙中间点坐标、尺寸、方向角确定。模型大小为100 m × 100 m，岩体裂隙条数共计2200条，其中J1 = 900条、J2 = 700条、J3 = 600条。

Figure 4. Random fracture model of rock mass of III2

图4. III2类岩体随机裂隙模型

4. 裂隙岩体渗流各向异性及表征单元研究

裂隙岩体的渗透性与裂隙网络的发育程度密切相关，研究表明，岩体渗透性往往比裂隙网络渗透性小数个数量级，因此，在研究岩体渗透性时，可忽略岩体基质透水作用，着重研究裂隙网络影响。裂隙发育的随机性造成了岩体渗透的各向异性，在不同的岩体模型尺寸下展现出不同的渗透特性，随着模型尺寸的增大，岩体各方向渗透性逐渐趋于稳定，在达到某个尺寸时可消除尺寸效应，使用连续介质来表征裂隙岩体平均渗透性，而这个尺寸即为裂隙岩体渗透REV。

4.1. 裂隙渗流理论

随机裂隙网络是岩体中渗流的主要通道，而单裂隙又是裂隙网络的组成部分，因此研究裂隙网络渗流的基础为研究单裂隙渗流。

由于岩体渗流通道的复杂性，在早期的研究中往往将岩体裂隙等效为光滑平板裂隙，前苏联学者Ломизе根据大量试验成果分析得到单裂隙渗流的立方定律，即单条裂隙的渗流量与裂隙开度的三次方成正比，裂隙单宽渗流量表示为：

$q=\frac{g{b}_E{}^3}{12\mu }I$ (1)

式中：q为裂隙单宽渗流量；g为重力加速度；b_E为隙宽；μ为水流动力粘度；I为水力坡降。

相应的水力传导系数为：

$K=\frac{g{b}_E{}^2}{12\mu }$ (2)

立方定律作为早期的研究成果获得了大量的应用，但同时也存在一些不足，Tsang [14] 指出由于裂隙开度变化和存在非贯通区域，不能假设为层流。后续诸多学者通过不同类型的试验说明立方定律仅适用于描述两壁光滑、开度较大、无填充物的单裂隙。为了考虑裂隙粗糙度、开度变化对渗透性的影响，诸多学者通过引入水力隙宽b来修正立方定律。Witherspoon [15] 建议用典型结构面测得的最大开度、裂隙面开度概率函数进行修正，得到了如下形式的广义流动定律。

$\frac{Q}{\Delta h}=\frac{C}{f}{\left(b\right)}^n$ (3)

式中：f为结构面粗糙度系数， $C=\rho g\omega /12\mu$ ， $\omega$ 为过水断面面积。当n取3时，公式3变为立方定律，水力隙宽和力学隙宽存在如下关系 $b=f^{1/3}{b}_h$ 。Barton等 [11] 则基于结构面粗糙度系数JRC和节理平均开度提出经验公式：

$b_h=\frac{b_E^2}{JR{C}^{2.5}}$ (4)

式中：b_h为力学隙宽，b_E是结构面的真实隙宽，b_E≥b_h。

4.2. 等效渗透张量计算

以二维离散裂隙网络为研究对象，探究裂隙随机分布在空间上的各向异性规律，裂隙岩体的各向异性往往用渗透张量来进行表示。对于均质各向异性介质，由达西定律可知，其内部渗流速度与水力梯度呈线性关系：

$v_i=K_{ij}{I}_j$ ， $i=1,2,3$ ； $j=1,2,3$ (5)

在三维问题中，K_ij为三阶渗透张量，可记作[K]，在总体坐标系中可表示为下列形式，根据渗透张量是一对称张量，因此可以通过旋转坐标轴得到对角张量，即：

$K=\left[\begin{array}{ccc}{k}_{11}& k_{12}& k_{13}\\ k_{21}& k_{22}& k_{23}\\ k_{31}& k_{32}& k_{33}\end{array}\right]\Rightarrow K=\left[\begin{array}{ccc}{k}_1& 0& 0\\ 0& k_2& 0\\ 0& 0& k_3\end{array}\right]$ (6)

式中，k₁、k₂、k₃为渗透张量主值，等于渗透张量矩阵特征值的大小，对应的特征向量的方向即为渗透主方向。

根据Bear [16] 的研究可知，裂隙岩体渗流本质上是研究水在裂隙网络中的流动，裂隙岩体在稳定的渗流条件下，渗透性满足：

$K_g=\frac{v_i{n}_i}{I}$ (7)

式中，K_g为沿着梯度方向的方向渗透系数，n_i为梯度方向的单位矢量的分量，其余符号意义同前式。

将式(7)带入达西定律得到：

$K_g=K_{ij}{n}_i{n}_j$ (8)

由上式两边同除以K_g，可得：

$1=K_{ij}\frac{n_i}{\sqrt{K_g}}\frac{n_j}{K_g}$ (9)

将 $\frac{n_i}{\sqrt{K_g}}=x_i$ 作为自变量，则上式可变为：

$1=K_{ij}{x}_i{x}_j$ (10)

式(10)在二维中表示为椭圆方程，i、j取值为1、2，k₁、k₂为渗透主值， $1/\sqrt{k_1}$ 、 $1/\sqrt{k_2}$ 为椭圆的长短轴半轴长。

在得到渗透椭圆及k₁、k₂、α后，可进一步计算渗透椭圆标准差RMS，用来判定能否用拟合得到的渗透椭圆描述裂隙岩体渗流各向异性特征。

$RMS=\frac{2}{k_1+k_2}\sqrt{\frac{1}{N}{{\displaystyle \underset{1}{\overset{N}{\sum }}\left[k_a\left(\theta \right)-k_b\left(\theta \right)\right]}}^2}$ (11)

式中，N为计算得到的渗透系数个数，θ为模型旋转角度，k_a(θ)是角度为θ时计算渗透系数，k_b(θ)是角度为θ时拟合渗透系数。

根据RMS值可判断渗透各向异性椭圆与椭圆曲线的拟合程度。只有当RMS ≤ 0.2时，裂隙网络模型可视为各向同性，等同于连续介质，此时对应的模型尺寸可作为该裂隙网络模型的REV。

4.3. 渗流表征单元体(REV)研究

裂隙岩体渗透性具有显著的尺寸效应，其渗透系数大小会随着模型尺寸的变化而变化，当模型尺寸较小时，随着尺寸的变化，渗透系数变化明显，当尺寸超过某一值时，渗透系数趋于稳定，而这个临界值所对应的尺寸即为该裂隙网络模型REV。

本节基于前述主洞室裂隙特征所生成二维随机裂隙网络模型，截取模型中心位置不同尺寸的试样进行计算。许多学者对REV尺寸与裂隙迹长的关系展开研究，但研究结论具有较大的差异性，卢波等 [17] 认为REV应大于裂隙迹长的3倍，张贵科 [5] 认为REV应为裂隙迹长的3~4倍。因此，最终计算尺寸应小于迹长3倍，大于迹长4倍，截取试样尺寸分别为20 m × 20 m、30 m × 30 m、40 m × 40 m、50 m × 50 m、60 m × 60 m、70 m × 70 m、80 m × 80 m、90 m × 90 m、100 m × 100 m、110 m × 110 m、120 m × 120 m，此外，为了得到模型的渗透主方向，对每一尺寸的模型按逆时针方向依次旋转30˚，共计12个方向(如图5所示)，并计算其渗透系数，不考虑应力作用对渗流影响。

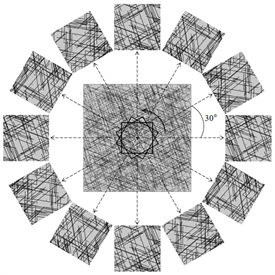
Figure 5. REV calculation model of fractured rock mass

图5. 裂隙岩体REV计算模型

模型边界条件设置如图6所示，上下边界均设置定水头边界，上边界为高水头边界，下边界为低水头边界，左右边界均设置为不透水边界，计算其流场稳定后的渗流速度，通过达西定律计算得到模型的渗透系数。

Figure 6. Boundary setting of seepage model

图6. 渗流模型边界设置

图7为不同尺寸、不同角度下模型平均渗透系数曲线图，从图中可以看出，当尺寸较小时，模型渗透系数波动较大，总体呈现逐渐增大的趋势，存在明显的尺寸效应，当尺寸达到100 m × 100 m时，方向渗透系数趋于稳定，此时模型渗透系数可代表库址区主洞室裂隙岩体的平均渗透性。

Figure 7. Permeability coefficient curves for different dimensions model directions

图7. 不同尺寸模型方向渗透系数曲线图

Figure 8. Elliptic diagram of directional permeability coefficient of different size models

图8. 不同尺寸模型方向渗透系数椭圆图

图8为不同尺寸裂隙岩体各个方向渗透系数椭圆图，由图可知，岩体主要渗透方向集中在60˚附近，为了得到各个尺寸下的渗透主值及方向角，将计算得到的渗透系数取其平方根的倒数作为坐标点，在极坐标系中用椭圆曲线进行拟合(如图9所示)，求出椭圆的长短轴长度，从而得到不同尺寸裂隙模型的渗透主值k₁、k₂，主值与极坐标系0˚方向夹角即为方向角(表4)。

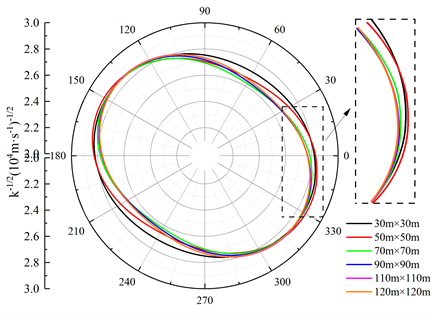
Figure 9. Permeability ellipse diagram of different size models

图9. 不同尺寸模型渗透椭圆示意图

Table 4. Results of permeability tensor calculation for models of different sizes

表4. 不同尺寸模型渗透张量计算结果

通过计算RMS值小于0.2，说明拟合渗透椭圆可以表征裂隙岩体渗透性，渗透主值方向角最终稳定在50.14˚，图10为渗透主值及方向角随模型尺寸变化曲线图，从图中可以看出，渗透主值及方向角在模型尺寸达到100 m后趋于稳定，因此，本文确定110 m × 110 m为裂隙模型渗透REV，当模型尺寸大于或等于110 m时，模型渗透性即可代表区域岩体平均渗透性。

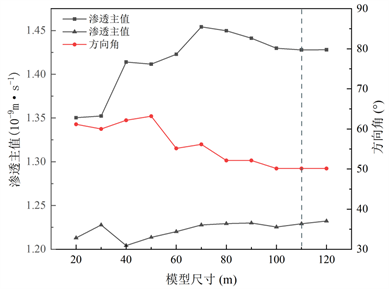
Figure 10. The principal value and direction Angle of penetration change with the model size

图10. 渗透主值及方向角随模型尺寸变化曲线图

5. 结论

本文根据库区现场地质素描采集到的主洞室层岩体裂隙数据，对裂隙岩体渗流力学特性展开研究，得到了如下结论：

1) 通过统计分析主洞室地质素描裂隙数据，得到主洞室层岩体裂隙分布特征。倾向、倾角服从正态分布，裂隙迹长、隙宽服从幂律分布，裂隙位置服从均匀分布。三组优势裂隙产状分别为：128˚ $\angle$ 76˚ (J1)、112˚ $\angle$ 72˚ (J2)、307˚ $\angle$ 53˚ (J3)。

2) 根据主洞室层岩体裂隙分布特征，利用MATLAB编写程序建立二维离散裂隙网络模型，通过控制模型尺寸和方向，计算库区岩体渗流REV尺寸、渗透张量及方向角大小，得到岩体渗透REV为110 m × 110 m，渗透主值k₁ = 1.43 × 10⁻⁹ m/s、k₂ = 1.23 × 10⁻⁹ m/s，方向角为50.12˚。

基金项目

国家自然科学基金项目(42207201)。

NOTES

^*第一作者。

^#通讯作者。