1. 引言
数学焦虑(mathematics anxiety)是指个体遇到与算术或数学有关的问题时产生的紧张和焦虑情绪(Suárez-Pellicioni et al., 2016),这种情绪在日常生活和学术情境中都很常见(Mammarella, Caviola, & Dowker, 2019)。由于不喜欢数学甚至讨厌数学,数学焦虑个体在日常生活中往往会忽视数学的重要性,在学习中经常会过分担心数学考试失败,进而逃避与算术或数学有关的任务(Rozgonjuk et al., 2020),最终导致数学焦虑个体的数学能力变得越来越低(Namkung, Peng, & Lin, 2019; Gabriel, Buckley, & Barthakur, 2020),而这又进一步加剧了数学焦虑(Maloney, 2016)。虽然数学焦虑个体在涉及到算术或数学时的表现比正常个体差,但是他们在其他类型的思维和推理任务中的表现往往与正常个体没有差异。而且,一方面,在进行简单的加法或乘法运算时,很难看出数学焦虑个体与正常个体之间的差异;另一方面,当数学运算涉及进位运算等算术问题时,数学焦虑个体与正常个体之间的能力差异就会表现得非常明显(Ramirez, Shaw, & Maloney, 2018)。有研究者认为,数学进位运算需要借助工作记忆(working memory)才能完成(Torbeyns et al., 2018)。工作记忆是一种资源有限的核心认知系统,它可以使个体既能在遇到分心刺激时具有积极保持并加工原有信息的能力,又能具有同时完成一项信息认知操作任务与一项信息认知保持任务的能力(Bouchacourt & Buschman, 2019)。大量理论和实证研究发现,数学焦虑消耗了原本用于执行计算的工作记忆资源,使个体没有足够的工作记忆资源用于数学计算,因此干扰了数学能力,影响了个体的数学成绩(Ashcraft & Kirker, 2001; Miller & Bichsel, 2004; Young, Wu, & Menon, 2012)。例如,在一项考察数学焦虑与工作记忆之间关系的研究中(Ashcraft & Kirker, 2001),参与者在保持加工2个或6个字母时完成加法运算。结果发现,在低工作记忆负荷(2个字母)下,高、低数学焦虑者的数学任务错误率没有差异;在高工作记忆负荷(6个字母)下,高数学焦虑者的数学任务错误率明显高于低数学焦虑者。研究者指出,在高工作记忆负荷下,高数学焦虑者工作记忆能力差的原因是他们对数学任务的担忧(侵入性思维)占用了原本用于完成数学任务的工作记忆资源(工作记忆容量)。
侵入性思维占用工作记忆容量的认知过程可以通过阅读广度任务(reading span task)来考察。阅读广度任务要求被试在完成第一种认知加工任务(如记住单词或字母)的同时完成第二种认知加工任务(如理解句子)。Conway等人(2005)在关于阅读广度任务的综述中指出,“人的注意力不仅会受到外界事件的干扰,还会受到侵入意识的某些想法的干扰,这些想法会使人产生联想——继续引发其他影响注意力的想法。抵制这些自动诱发的想法和联想,不仅需要调节并保持注意力,而且还要调节并引导人的想法。阅读广度任务所测量的工作记忆容量就是这种调节并改善注意力与思维能力的心理与认知结构。”然而,由于传统阅读广度任务的两项认知加工任务使用的都是中性信息,而侵入性思维往往是具有情绪性的想法,因此使用传统阅读广度任务反映侵入性思维与工作记忆容量之间的关系具有一定的局限性(Schweizer & Dalgleish, 2011)。例如,一位患有创伤后压力障碍的女性在努力完成一项依赖工作记忆容量的复杂认知任务时,还需要排除占据大量工作记忆资源的、涉及创伤记忆的、痛苦的侵入性想法,这种情绪性的工作记忆容量竞争模式就很难用传统阅读广度任务来反映。
最近,一些研究者对传统阅读广度任务进行了修改,开发了一种情绪版阅读广度任务——将带有情绪性的材料引入阅读广度任务,创设出情绪性语境与中性语境(Schweizer & Dalgleish, 2011; Shi, Gao, & Zhou, 2014; Shi & Liu, 2016)。这些研究者使用情绪版阅读广度任务,发现创伤后应激障碍个体、考试焦虑个体以及数学焦虑个体在情绪性语境下的工作记忆容量远低于中性语境下的工作记忆容量。例如,Shi和Liu (2016)开展了一项考察大学生数学焦虑个体情绪性与中性语境下的工作记忆容量差异的研究。该研究通过句子加工来创设实验情境:情绪性语境通过加工与数学有关的情绪性句子来创设,比如,“当我做数学题时,我感到紧张。”中性语境通过加工与世界一般客观事实有关的中性句子来创设,比如,“太阳每天从东方升起,从西方落下。”情绪版阅读广度任务要求被试在记住中性字母的同时加工上述两类句子。结果表明,与低数学焦虑个体相比,高数学焦虑个体在情绪性语境下的工作记忆容量比在中性语境下的工作记忆容量低。
Shi和Liu (2016)的研究与Ashcraft和Kirk (2001)的研究有以下不同之处。Ashcraft和Kirk (2001)只是测试了当认知任务涉及算术或数学运算时,数学焦虑会干扰工作记忆,并没有测试情绪性的侵入性思维对工作记忆容量的影响。Ashcraft和Kirk (2001)有可能忽略了工作记忆容量受损的主要原因——与数学有关的侵入性思维占用工作记忆容量。与Ashcraft和Kirk (2001)的任务不同,Shi和Liu (2016)不仅考察了与数学有关的情绪性侵入性思维对工作记忆容量的影响,而且其使用的任务不涉及算术或数学相关加工,这说明了具体的数学运算不一定是影响数学焦虑个体工作记忆容量的主要原因,而工作记忆容量被与数学有关的情绪性侵入性思维占用有可能是数学焦虑个体工作记忆容量受影响的主要原因。
Shi和Liu (2016)考察了数学焦虑与成年人(大学生)工作记忆容量的关系,并没有从发展的角度进一步考察这一问题。迄今为止,非常多的研究试图探究数学焦虑的发生与发展的根本原因,然而业界并没有就这一问题达成一致。因此,有必要在数学焦虑影响成年人工作记忆容量这一研究基础上,从发展的角度对数学焦虑与工作记忆容量之间的关系作进一步的探讨,以便深刻理解数学焦虑发生与发展的机制。
2. 方法
2.1. 被试
用数学焦虑量表筛选出高数学焦虑者63人(平均年龄为15.51 ± 0.67岁),低数学焦虑者64人(平均年龄为15.36 ± 0.68岁),共有127名初三学生参加了实验。根据Merrell (2000)的研究,数学焦虑筛选标准为±1个标准差,高数学焦虑为84.48 ± 7.07,低数学焦虑为41.59 ± 5.24,两组被试的数学焦虑分数存在显著差异,t(125) = −38.90,p < 0.001。为了排数考试焦虑的影响,用考试焦虑简表进行测量,所有被试均为低考试焦虑者。两组被试的考试焦虑分数差异不显著,t(125) = 1.25,p = 0.213。所有被试在实验前均填写了知情同意书。
2.2. 测量工具
2.2.1. 数学焦虑量表
数学焦虑量表采用由Plake和Parker (1982)对数学焦虑量表进行简化得到的修订数学焦虑量表(MARS-R)。MARS-R的中文版由刘效贞(2009)翻译为中文并投入使用。该量表包含21个项目,采用Likert 5级评分法,1表示“没有焦虑”,2表示“有点焦虑”,3表示“一般焦虑”,4代表“比较焦虑”,5代表“非常焦虑”,得分越高说明数学焦虑程度越严重。该量表具有较高的信度,内部一致性系数为0.93,重测信度为0.93。
2.2.2. 考试焦虑量表
考试焦虑量表采用董云英等人(2011)修订的考试焦虑简表,该量表包含5个项目,采用Likert 4级评分法,1表示“从不”,2表示“有时”,3表示“经常”,4代表“总是”,得分越高说明考试焦虑程度越严重。该量表具有较高的信度,内部一致性系数为0.91,重测信度为0.91。
2.3. 阅读广度任务
采用Shi和Liu (2016)的情绪版阅读广度任务测量数学相关语境和中性语境下的工作记忆容量。
首先,屏幕上呈现一个句子,要求被试大声朗读。实验情境通过不同的句子加工实现:数学相关语境通过加工与数学有关的情绪性句子来创设,比如,“当我做数学题时,我感到紧张。”中性语境通过加工与世界一般客观事实有关的中性句子来创设,比如,“太阳每天从东方升起,从西方落下。”两类句子随机呈现。
接着,屏幕上呈现一个提示“这个句子是否存在语序错误。”要求被试判断“是”或者“否”。每种语境下均有25%的句子包含一个语序错误,例如,“美丽”会被写成“丽美”。句子判断正确率要求在85%以上。
然后,屏幕上呈现一个字母,要求被试记住这个字母。字母消失后,出现下一个句子,下一个判断,下一个字母。一个句子和一个字母构成一个句子-字母对,一组任务可能包含3–5个句子-字母对,也即构成3试次任务、4试次组任务或5试次任务。
最后,屏幕上呈现一个包含12个字母的回忆界面,每个字母前面有一个选择框,要求被试按顺序选出之前看到的字母。实验采用全或无的计分规则,即一组任务只有当字母全部回忆正确记满分,如果出错则记为0。例如,对于3试次任务,如果3个字母全部按顺序回忆正确记为3,如果某个字母或字母顺序回忆错误,则记为0。采用全或无计分规则的原因在于,日常生活或学术工作中,只记住一半公式对解题没有任何帮助。
2.4. 实验过程
每个被试在实验室单独完成实验。首先,被试了解实验指导语并做练习;接着,被试完成阅读广度任务;最后,实验结束,被试离开实验室。
2.5. 实验设计
研究采用2 (组别:高数学焦虑组与低数学焦虑组) × 2 (语境:数学相关语境与中性语境)的混合设计,其中组别为组间变量,语境为组内变量。
2.6. 统计分析
使用SPSS 16.0软件进行统计分析。
3. 结果
3.1. 工作记忆容量
对工作记忆容量得分比率进行2 (组别:高数学焦虑组与低数学焦虑组) × 2 (语境:数学相关语境与中性语境)的重复测量方差分析。结果显示,组别主效应不显著,F(1, 125) = 2.61,p = 0.109。语境主效应显著,F(1, 125) = 35.61,p < 0.001,
= 0.22,进一步分析发现,数学相关语境下的工作记忆容量明显低于中性语境。组别与语境的交互作用显著,F(1, 125) = 41.90,p < 0.001,
= 0.25。简单效应分析发现,在数学相关语境下,高数学焦虑组的工作记忆容量显著低于低数学焦虑组,p < 0.001;在中性语境下,高数学焦虑组与低数学焦虑组的工作记忆容量不存在显著差异,p = 0.165。高数学焦虑组数学相关语境下的工作记忆容量显著低于中性语境下的工作记忆容量,p < 0.001;低数学焦虑组两种语境下的工作记忆容量不存在显著差异,p = 0.720。结果见表1。

Table 1. Working memory capacity under the mathematics related context and the neutral context for high-math-anxious group compared with low-math-anxious group
表1. 高、低数学焦虑组在数学相关语境和中性语境下的工作记忆容量
将被试在3试次任务、4试次任务和5试次任务上数学相关语境与中性语境下的工作记忆容量差距作为因变量,组别作为自变量进行多元方差分析。三组工作记忆容量指数的协方差矩阵相等,Box’s M = 7.35,p = 0.306,说明因变量可以进行多元方差分析。由于该分析为探索性分析,所以显著性需要矫正,p = 0.05/3 = 0.0167,即对于每一种试次任务而言,p < 0.017时达到显著性水平。结果显示,高数学焦虑组两种语境的工作记忆容量差距与低数学焦虑组存在显著差异,Wilk’s Lambda = 0.76,F(3,123) = 12.74,p < 0.001,
= 0.24。进一步分析发现,高数学焦虑组在4试次任务(F(1,125) = 7.69, p = 0.006)和5试次任务(F(1,125) = 23.12, p < 0.001)上两种语境下的工作记忆容量差距显著大于低数学焦虑组;而对于3试次任务,高数学焦虑组与低数学焦虑组的两种语境下的工作记忆容量差距不存在显著差异,F(1,125) = 3.18,p = 0.077。结果见图1。
3.2. 反应时
对句子判断反应时进行2 (组别:高数学焦虑组与低数学焦虑组) × 2 (语境:数学相关语境与中性语境)的重复测量方差分析。结果显示,组别主效应不显著,F(1, 125) = 0.28,p = 0.596;语境主效应不显著,F(1, 125) = 0.71,p = 0.401;语境与组别的交互作用不显著,F(1, 125) = 0.78,p = 0.378。
3.3. 正确率
对句子判断错误率进行2 (组别:高数学焦虑组与低数学焦虑组) × 2 (语境:数学相关语境与中性语境)的重复测量方差分析。结果显示,组别主效应不显著,F(1, 125) = 1.09,p = 0.299;语境主效应不显著,F(1, 125) = 0.07,p = 0.795;语境与组别的交互作用不显著,F(1, 125) = 1.41,p = 0.237。
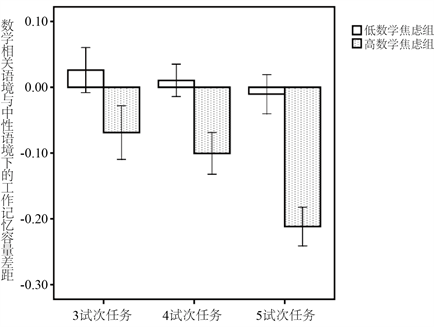
Figure 1. The differences between WMC scores for trials under the mathematics related context and WMC scores for trials under the neutral context for trial sizes 3~5 for high-math-anxious group compared with low-math-anxious group
图1. 高、低数学焦虑组在3~5试次任务上的数学相关语境与中性语境下的工作记忆容量差距
4. 讨论
本研究采用情绪版阅读广度任务考察了高、低数学焦虑个体在数学语境和中性语境下的工作记忆容量。与Shi和Liu (2016)的研究结果一致,本研究结果表明,高数学焦虑者在数学语境下的工作记忆容量比低数学焦虑者小,高数学焦虑者在数学语境下的工作记忆容量比在中性语境下的工作记忆容量小。在高工作记忆负荷(4试次任务和5试次任务)下,高数学焦虑者数学语境与中性语境下的工作记忆容量的差距比低数学焦虑者的差距大。然而在低工作记忆负荷(3试次任务)下,高数学焦虑者与低数学焦虑者两种语境下工作记忆容量的差距之间没有差异。此外,本研究没有发现数学焦虑对反应时间和准确度的影响。
在以往考察算术或数学运算与工作记忆容量之间关系的研究中(Ashcraft & Kirk, 2001; Klados et al., 2015),工作记忆容量受两种因素的干扰,一是算术或数学运算本身,二是算术或数学运算诱发的侵入性思维。然而,这些研究并没有对这二者进行区分。加工效能理论指出,对数学任务的担忧这一侵入性思维会占用原本用于完成数学任务的资源有限的工作记忆(Eysenck & Calvo, 1992)。本研究使用与数学有关的情绪性句子创设数学语境,考察了由数学语境诱发的侵入性思维对工作记忆的影响,排除了算术或数学运算本身对工作记忆的影响。本研究结果既丰富了以往研究结果,又支持了加工效能理论的观点。在日常生活中,我们时常会经历一些负性事件,尽管这些负性事件已经结束,但当我们经历类似的事情或者看到一些与该事情有关的提示时,关于这些负性事件的记忆依然会浮现于脑海进而会对正在完成的任务产生干扰。正如在本研究中,给高数学焦虑个体呈现一些与数学有关的情绪性句子时,高数学焦虑个体就会产生对数学担心的侵入性思维,这些侵入性思维会占用原本用于记忆字母的工作记忆资源,导致记忆字母的成绩较低。而且随记忆字母个数增加,这种影响也随之增加。
从本研究的结果可以推论出,两种技术路径可以有效预防数学焦虑对工作记忆容量的影响:1) 减少数学焦虑个体对数学任务的担忧;2) 增加焦虑个体在数学相关语境下的工作记忆容量。这两种技术路径可以通过以下两种干预方法实现。一种干预方法是书写表达。例如,学生在参加数学考试前花几分钟时间写出自己的感受。研究者认为,通过写作来减少负面情绪,可以有效减少学生在考试期间对数学失败的担忧,释放工作记忆资源,这对完成复杂任务至关重要(Park, Ramirez, & Beilock, 2014)。另一种干预方法是认知重构(Ramirez et al., 2018)。例如,高度的生理唤醒诸如出汗、心跳加速等通常被看作是紧张的表现,而认知重构方法教会学生重新认识高度的生理唤醒:高度的生理唤醒既意味着即将取得成功,又对思考和推理有促进作用。关于认知重构的研究发现,对生理唤醒的再评估或者对生理唤醒的重新解释可以有效降低侵入性思维的干扰(Jamieson et al., 2016)。
从某种意义上说,侵入性思维占用工作记忆容量可以被看作是两种相互冲突的心理加工对工作记忆资源竞争的过程。本研究采用情绪版阅读广度任务不仅使得这两种冲突的心理加工具有可操作性,而且准确测量了数学焦虑个体在数学语境下的工作记忆容量,验证了情绪版阅读广度任务的有效性。未来研究可以在本研究的基础上将这一范式应用到更多的学习或工作情境中,创设出更多情绪性语境的阅读广度任务,考察其他情绪障碍个体的工作记忆容量受损情况。另外,本研究的结果具有一定的教育意义。例如,很多老师会认为高数学焦虑的学生作业成绩一定不好。然而,从本研究结果可以看出,高数学焦虑的学生只是在数学语境下作业成绩变差;在涉及中性信息的语境下,他们的作业成绩不受影响。教师或许可以通过对这个问题的思考,掌握辩证看待学生不同作业成绩的方法和原理。
本研究仅考察了数学语境诱发的侵入性思维对高数学焦虑者工作记忆容量的影响,没有考察算术或数学运算对工作记忆容量的影响。未来应发展更精细的研究范式,可以同时考察算术或数学运算本身以及其诱发的侵入性思维对工作记忆容量的影响,并探究二者之间的关系,这样才能更清楚地了解数学焦虑与工作记忆之间的关系。
基金项目
琼台师范学院科研平台项目“琼台师范学院特殊儿童认知康复研究中心(QTPT21-4)”。