1. 研究背景及国内外发展趋势
在当下全球化的国际社会中,无论是个人之间还是国家之间,合作共赢已成为国际共识,这都说明了合作行为在人类社会进步、文明发展历程中的重要性。自然界中合作现象是普遍存在的。例如鳄鱼–千鸟互惠互利、榕树–榕小蜂互惠互利、狼群的捕猎合作现象、海葵–小丑鱼互惠互利以及鰕虎鱼–枪虾互惠互利 [1] [2] ,合作行为可以简单理解为:一个个体可以牺牲自己的一部分利益为其他人带来利益 [3] 。相比之下适者生存准则所表现的是个体追求自身最大化的利益及一种自私行为,如此普遍存在的合作行为与达尔文的自然学说相矛盾,引起了社会学、经济学以及生物学等多个领域的关注。合作现象对于现在来说虽然极其普遍,但是基于理性人的角度,反社会行为才是利益最大化的决策,因此研究合作是如何演化的是十分重要的。
演化博弈论作为一个框架,揭示了为什么以及如何在有缺陷的环境中合作盛行。为了探究自私种群中合作行为是如何出现并维持的,基于演化博弈论这个强有力的研究框架,Nowak总结了促进合作演化的五种机制:亲缘选择、直接互惠、间接互惠、网络互惠和群体选择 [4] [5] 。基于Nowak等学者的研究结果,一些经济学家和社会学家将运用演化博弈论来解决社会困境的问题 [6] ,其中社会困境可归纳于个人对于个人利益最大化与集体利益最大化之间的选择矛盾,取得了丰硕的成果。
在上述社会困境问题中存在一种被称为搭便车的行为。相较于亲社会性的合作者,搭便车者往往只关注自身利益而对于集体利益没有贡献,这会极大影响社会中的产出,如何解决这种搭便车行为是我们研究的核心问题。一些研究表明,解决搭便车行为可以通过惩罚行为来对其进行约束 [7] [8] 。惩罚意味着惩罚者愿意付出一定的成本使得被惩罚者损失一部分的收益,往往被惩罚者损失的收益大于惩罚者的成本,因此惩罚可以认为是解释社会合作行为的有效机制。但在使用惩罚时惩罚者会付出代价高昂的成本,这最终会导致自己总收益的减少,因此先前已经有大量研究证明代价高昂的惩罚并不能总是促进合作的演化 [9] [10] 。为了解决惩罚成本高昂的问题,不少研究已经提出了基于条件惩罚的机制,条件惩罚区别于直接惩罚,而是在达到一定条件之后再对个体进行惩罚,这样既可以解决种群中的搭便车问题,又可以增加自己的收益,实现“双赢”的局面。例如,对个体惩罚的力度与叛逃者的人数成比例 [11] 、与其他成员对该个体的处罚决策成比例等都是条件惩罚的例子 [12] [13] 。这种条件惩罚是我们关注的重点,其在现实中极为普遍。
另外,最近的理论研究表明,惩罚是在声誉博弈的背景下发展起来的 [14] [15] 。简单来说,可以用声誉来区分惩罚者和非惩罚者,惩罚者通过利他主义惩罚积累自己的声誉,从而更有可能在未来的互动中获得帮助。同样地,如果个体与种群中与其他成员博弈时选择叛逃的策略,那么我们就可以减掉其拥有的声誉分,如此一来,声誉分值越低,表明个体在与其他成员互动时叛逃的次数越多,那么惩罚者在选择惩罚力度时就可以根据叛逃者的声誉分来决定,声誉分值越低,则惩罚力度越强,可以在一定程度上解决传统惩罚代价高昂的问题。总的来说,声誉在种群合作中起着十分关键的作用。
因此,在本文的模型中,我们将基于个体声誉和组平均声誉的机制上考虑条件惩罚对合作演化的影响。
2. 模型
2.1. 空间公共物品博弈
在本文的模型中考虑了空间公共物品博弈(SPGG),该博弈发生在一个L*L的具有周期边界的格子网络上。在该网格上,每个节点表示一个玩家i,并有四条连接的边,代表中心玩家i的四个邻居。在结构化种群中,由玩家i和四个邻居组成的五个玩家被视为一个玩公共物品博弈的群体。因此,每个玩家在每个时间步长总共参与五轮公共物品博弈。在该博弈中,有合作者(简称C)、叛逃者(简称D)和惩罚者(惩罚合作者,简称PC)三种策略,并在模拟初始化时给玩家随机分配这三种策略。
2.2. 基于声誉的条件惩罚机制
本模型假定叛逃个体i受到惩罚的概率主要取决于他的声誉水平
以及他邻居的平均声誉
。具体如下,我们引入个体i邻居的平均声誉
乘上折扣因子
作为动态声誉阈值,该阈值将玩家分为两种不同的类型:对于声誉高于阈值
的叛逃个体i而言可以认为是“好”玩家,因此不用受到惩罚者的惩罚;而对于声誉低于阈值
的叛逃个体i而言则被认为是“坏”玩家,因此依据其具体声誉有一定概率会受到惩罚,且受到惩罚的概率与他的声誉水平
呈负相关。基于此,叛逃个体i受到惩罚的概率可以写成等式(1),其中用
来表示惩罚概率:
(1)
其中参数b影响惩罚的强度。如果声誉
保持不变,则叛逃者
受到惩罚的概率随着b的值的减小而增大。这意味着b值越小,惩罚强度就越大,惩罚者对叛逃行为的容忍度就越低。
2.3. 声誉更新机制
在模拟时将每个玩家的声誉进行初始化,即在[0, Rmax]中随机为所有玩家分配一个声誉。在演化过程中,玩家声誉的更新方式是与玩家采取的策略和时间相相关的。具体的更新规则可以写成如下等式(2),其中
表示玩家的策略:
(2)
由于玩家声誉值是被限制在[0, Rmax]的范围内,那么对于玩家i,如果
的值超过Rmax,那么我们假设
。类似地,如果
小于0,那么
。
2.4. 玩家i的收益计算
在每一轮空间公共物品博弈中,每个合作者或每个惩罚者都会向公共池贡献一个单位的资源,但叛逃者什么也不贡献。C和PC玩家的所有贡献都乘以增强因子r (r > 1),然后平均分配给所有玩家。除玩家收到的公共池的收益之外,D玩家还因受到PC玩家的惩罚而付出罚金,同样地,PC玩家也会因此付出惩罚成本。因此,玩家每进行一次公共物品博弈的具体收益计算公式(3)如下:
(3)
在上式中,
代表叛逃玩家i在一次公共物品博弈中受到的惩罚次数,
代表叛逃玩家 每次受到惩罚时需付出的罚金。
代表惩罚玩家i在一次公共物品博弈中要惩罚的次数,
代表惩罚者惩罚一次叛逃者所付出的惩罚成本。对于玩家i而言,累积收益
来自他自己和他的四个邻居组织的五轮博弈收益的总和。
2.5. 策略更新机制
本文假设玩家使用费米规则异步更新他们的策略。具体如公式(4):
(4)
该费米更新规则意味着当随机选择的玩家i的邻居j的收益比玩家i高时,那么玩家i模仿玩家j策略的概率就越高。其中K表示选择强度,当K趋于0时,玩家i更倾向于选择收益更高的策略,当K趋于
时,玩家i策略更新是完全随机的。综合考虑,该模型选择K = 0.5。
2.6. 合作率
本文引入了等式(5)的合作水平来描述种群的进化状态,其中
和
分别代表种群中合作者和惩罚者的数量
(5)
3. 模型结果及分析
首先,我们研究了在声誉阈值的不同设定值下,增强因子r如何影响合作的演变。从图1中可以看出,对于任何给定的fai值,随着r从0增加到5.6,合作水平
都呈增加趋势。也就是说,r的值越大,越有利于促进合作,这一观察结果意味着,合作行为回报的增加会导致采取合作行动的意愿增加。此外,如图1所示,在不同的fai值下,合作的演变是显著不同的。具体而言,对于极端值fai = 1,当r从0增加到5.6时,合作水平显著增加,然后达到完全合作。但是对于fai = 0.9、fai = 0.8、fai = 0.6、fai = 0.3、fai = 0.1,相较于fai = 1,在r = 2.4及以上合作才会出现,并且达到完全合作较晚。该分析结果在Rmax = 80和Rmax = 100的相图中都是相似的。综合考虑将在其他结果中都使用Rmax = 100。
综上所述,图1的结果表明,对于任何给定的r值,fai值越高,越有利于合作的出现和促进。从以上结果可以看出,fai值越高,种群进入ESS的速度就越快。事实上,fai的值越高,意味着结构化人群中有更多的玩家被认为是坏玩家,如果他们采用D策略,他们更有可能受到惩罚。这是因为在进化过程中,较高的fai值有利于合作,而不是叛逃的行为。

Figure 1. For six different reputation thresholds, cooperation rate
as a function of the enhancement factor r. (a) Rmax = 80; (b) Rmax = 100. Other parameters are α = 0.1, b = 0, β= 1.0, L = 100, with a time step of 104
图1. 对于六个不同的声誉阈值,合作率
作为增强因子r的函数。(a) Rmax = 80;(b) Rmax = 100。其他参数为α = 0.1、b = 0、β = 1.0,L = 100,时间步长为104
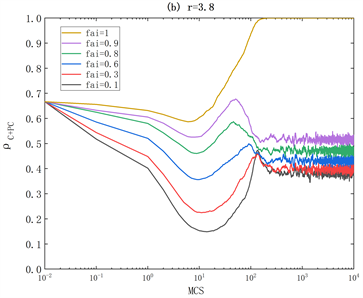
Figure 2. For six different reputation thresholds, the process of cooperation rate
evolving over time. (a) r = 3.0; (b) r = 3.8. Other parameters are α = 0.1, b = 0, β = 1.0, Rmax = 100, L = 100, with a time step of 104
图2. 对于六个不同的声誉阈值,合作率
随时间演化的过程。(a) r = 3.0;(b) r = 3.8。其他参数为α = 0.1、b = 0、β = 1.0,Rmax = 100,L = 100,时间步长为104
在图2中,我们进一步研究了合作水平
是如何随着时间步长t演变的。图2(a)显示了
在r = 3的不同声誉阈值fai下的演变动力学。图中的结果2(a)表明,虽然不同的fai值在时间前期演化趋势相同,合作率都从t = 1显著下降到t = 80,但是从t = 80到t = 100的演化趋势显著不同,当fai = 1时合作率最终达到1的稳定状态,当fai = 0.6、fai = 0.3、fai = 0.1时合作率最后降为0,当fai = 0.8、fai = 0.9时合作率呈震荡的趋势。
此外,在图2(b)我们研究了r = 3.8时的合作动力学。如图所示,对于任何给定的fai值,在进化稳定状态下,合作的性能更好。这些结果进一步验证了我们在图1中观察到的情况。

Figure 3. A strategy spatial distribution map of four representative time steps with different reputation thresholds and enhancement factors. (a) fai = 1, b = 0, r = 3.8; (b) fai = 1, b = 0, r = 3.0; (c) fai = 0.9, b = 0, r = 3.8; (d) fai = 0.8, b = 0, r = 3.8. Other parameters are α = 0.1, β = 1.0, Rmax = 100, L = 100. Green represents the punisher, blue represents the defector, and red represents the cooperator
图3. 不同声誉阈值和增强因子的四个代表性时间步长的策略空间分布图。(a) fai = 1,b = 0,r = 3.8;(b) fai = 1,b = 0,r = 3.0;(c) fai = 0.9,b = 0,r = 3.8;(d) fai = 0.8,b = 0,r = 3.8。其他参数为α = 0.1、β = 1.0,Rmax = 100,L = 100。绿色代表惩罚者,蓝色代表叛逃者,红色代表合作者
在图3中,我们比较了C、D、PC这三种策略的空间演化分布,以进一步探讨声誉阈值如何影响种群的合作水平。如图3所示,在四种不同参数的演化过程中,策略在空间上的分布是处于进化稳定状态的集群。具体而言,在fai = 1的时候,无论r = 3.0或r = 3.8,集群在演化最后都能达到全合作的状态,这是因为fai值较大的时候,对叛逃者的容忍度比较低,所以叛逃者不能够稳定存在。另外,在t = 80的时候,可以明显观察到r = 3.8时是惩罚者占主导地位,而r = 3.0时是叛逃者占主导地位,这是因为如果增强因子较小,对合作的促进作用相对较差。而在fai值较小的时候,例如图3(c)和图3(d),此时最终稳态是D、PC共存,这是因为fai值较小时对叛逃者的容忍度较高,所以叛逃者能够稳定存在。
为了讨论声誉阈值对个体声誉分布的影响,我们比较了个人声誉空间演化分布图。如图4所示,从声誉分布的角度来看,声誉阈值越大,平均声誉水平处于稳定状态的程度就越高。在fai = 1时由于阈值较高对叛逃者的容忍度低,因此叛逃者较少,在t = 2000时基本上只有惩罚者和合作者,因此声誉值能达到100。相较而言,当fai = 0.9和fai = 0.8时,虽然达到稳态时既有惩罚者、合作者又有叛逃者,但是因为其阈值还是相对较高,所以叛逃者占比例较少,其空间声誉分布与图4(a)相似。此外,对于fai = 0.3的较低声誉阈值,图中的结果如图4(d)所示,低声誉个体从t = 80到t = 2000逐渐占据种群。
综上,根据结果我们可以发现,基于声誉的条件惩罚机制不仅可以驱逐叛逃者,还可以帮助策略为PC或C的合作玩家建立良好的声誉。
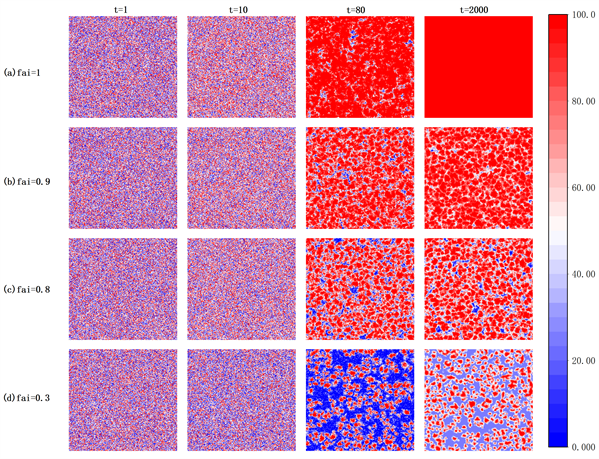
Figure 4. The spatial distribution of individual reputation at four representative time steps under four different parameter conditions. (a) fai = 1, b = 0, r = 3.8; (b) fai = 0.9, b = 0, r = 3.8; (c) fai = 0.8, b = 0, r = 3.8; (d) fai = 0.3, b = 0, r = 3.8. The color bar associates the reputation values corresponding to different colors. Other parameters are α = 0.1, β = 1.0, Rmax = 100, L = 100
图4. 在四种不同参数条件下,个体声誉在四个代表性时间步长的空间分布图。(a) fai = 1,b = 0,r = 3.8;(b) fai = 0.9,b = 0,r = 3.8;(c) fai = 0.8,b = 0,r = 3.8;(d) fai = 0.3,b = 0,r = 3.8。颜色条将不同颜色对应的信誉值关联起来。其他参数为α = 0.1、β = 1.0,Rmax = 100,L = 100
在图5中,我们进一步研究了信誉阈值如何影响收益的空间演变和分布。如图5所示,fai值将影响进化稳定状态下的平均收益水平。具体而言,在fai = 1时由于阈值较高对叛逃者的容忍度低,因此叛逃者较少,在t = 2000时基本上只有惩罚者和合作者,因此个体收益都能达到最高。相较而言,当fai = 0.9、fai = 0.8和fai = 0.3时,空间分布中存在两种不同类型的集群,即高收益集群和低收益集群。高收益的个体被高收益的个体包围,而低收益的个体被低收益的个体包围。出现这种现象的原因是不同的声誉阈值对应于对背叛行为的不同容忍度不同。
综上,上述结果意味着基于声誉的条件惩罚机制通过保证采用PC策略或C策略的玩家的更高回报来促进合作。

Figure 5. The spatial distribution of individual returns at four representative time steps under four different parameter conditions. (a) fai = 1, b = 0, r = 3.8; (b) fai = 0.9, b = 0, r = 3.8; (c) fai = 0.8, b = 0, r = 3.8; (d) fai = 0.3, b = 0, r = 3.8. The color bar associates the reputation values corresponding to different colors. Other parameters are α = 0.1, β = 1.0, Rmax = 100, L = 100
图5. 在四种不同参数条件下,个体收益在四个代表性时间步长的空间分布图。(a) fai = 1,b = 0,r = 3.8;(b) fai = 0.9,b = 0,r = 3.8;(c) fai = 0.8,b = 0,r = 3.8;(d) fai = 0.3,b = 0,r = 3.8。颜色条将不同颜色对应的收益关联起来。其他参数为α = 0.1、β = 1.0,Rmax = 100,L = 100

Figure 6. Cooperation rate
is a function of the enhancement factor r for different values of b. Other parameters are α = 0.1, β = 1.0, fai = 1, L = 100, Rmax = 100, with a time step of 104
图6. 合作率
是b的不同值的增强因子r的函数。其他参数为α = 0.1、β = 1.0,fai = 1,L = 100,Rmax = 100,时间步长为104
在图6中,我们接着研究了对于代表惩罚强度的不同b值,增强因子r如何影响合作演变。观察图我们可以发现,对于任何给定的b值,随着r从0增加到5.6,合作率都呈现增加趋势。此外,对于b的五个不同值,合作的演变表现出显著差异,当b值越小时,对于合作水平的促进作用越强。出现上述结果的原因是较小的b值意味着较高的惩罚成本,可以有效地防止玩家采取叛逃的行为。
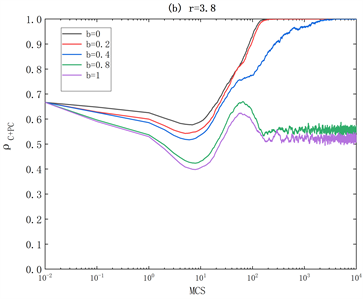
Figure 7. Time evolution of cooperation rate
under different penalty intensities b. (a) r = 3.0; (b) r=3.8. Other parameters are α = 0.1, β = 1.0, fai = 1, L = 100, Rmax = 100, with a time step of 104
图7. 不同的惩罚强度b下的合作率
的时间演化图。(a) r = 3.0;(b) r=3.8。其他参数为α = 0.1、β = 1.0,fai = 1,L = 100,Rmax = 100,时间步长为104

Figure 8. The spatial distribution of different penalty intensities b and enhancement factor r in four representative time steps. (a) fai = 1, b = 0, r = 3.0; (b) fai = 1, b = 0.4, r = 3.0; (c) fai = 1, b = 0.8, r = 3.0; (d) fai = 1, b = 1.0, r = 3.0. Other parameters are α = 0.1, β = 1.0, L = 100, Rmax = 100. Green for punisher, blue for defector, red for cooperator
图8. 不同惩罚强度b和增强因子r在四个代表性时间步长的策略空间分布图。(a) fai = 1,b = 0和r = 3.0;(b) fai = 1,b = 0.4,r = 3.0;(c) fai = 1,b = 0.8,r = 3.0;(d) fai = 1,b = 1.0,r = 3.0。其他参数为α = 0.1、β = 1.0,L = 100,Rmax = 100。绿色代表惩罚者,蓝色代表叛逃者,红色代表合作者
在图7中,我们进一步探索了对于不同的惩罚强度b值和增强因子r值,合作率如何随着时间步长t而演化。通过观察图7(a)可知,虽然不同的b值在时间前期演化趋势相同,合作率都从t = 1显著下降到t = 80,但是从t = 80到t = 100的演化趋势显著不同,当b = 0和b = 0.2时合作率最终达到1的稳定状态,当b = 0.4、b = 0.8和b = 1时合作率呈震荡的趋势,并且合作率逐渐减少。
此外,在图7(b)我们研究了r = 3.8时的合作动力学。如图所示,对于任何给定的b值,在进化稳定状态下,合作的性能更好。这些结果进一步验证了我们在图6中观察到的情况。
在图8中,我们研究了不同参数下三种策略的空间演化分布图,以进一步探索惩罚强度b如何影响合作的动态。观察图8可知,策略在空间上的分布是进化稳定状态下集群的形式。当b值越小的时候,惩罚力度越强,叛逃者消失的速度越快,当b = 0时,达到了完全合作的状态,当b变大时,策略空间分布呈现惩罚者集群和叛逃者集群稳定存在,且b越大,叛逃者集群越多。出现这一现象的原因是b的不同造成了惩罚力度不同,b越大,惩罚力度越小,叛逃者更容易存在。
4. 结论
本文在SPGG模型中引入了一种新的机制——基于声誉的条件惩罚,并且还考虑种群效应。在这种机制中,玩家根据自己的声誉和邻居的平均收益分为两类,声誉高于声誉阈值的好玩家和声誉低于阈值的坏玩家。重要的是,该声誉阈值是由中心个体的四个邻居的平均收益决定,是与时间相关的动态阈值,与以往的研究有所不同。此外,我们还考虑到任何玩家的声誉都是随时间变化的,并根据特定规则进行更新。基于这些假设,我们系统地研究了这种机制如何影响合作的演变。
通过模拟,我们验证了基于声誉的条件惩罚机制有利于合作的发展。首先,更高的信誉阈值更有利于合作的出现和促进。事实上,更高的声誉阈值意味着,如果采用D策略,更多被认为是坏玩家的玩家更有可能受到惩罚。此外,增加惩罚强度可以有效地鼓励玩家参与合作行为。
基金项目
云南省教育厅科学研究基金项目(V2023) (项目编号:2023Y0661)。