1. 引言
在数学的研究中，特别是函数论的研究中，对应是一个最基本的概念。它不仅是我们研究两个集合或者物体关系的桥梁，也为我们有目的地做事情、合理地选择研究事物的母体、以及研究的方法等，提供了一种选择的可能。例如，如果在两个集合中建立了对应关系，我们就可以原像集、对应关系、像集，这三位一体的有机体中，合理的选择其中的两者，而寻找第三者的信息。当然，我们事先必须对这些参与者，提出一定的规范性要求。
在所有的对应中，一一对应是最理想的对应。因为这个对应可以实现一个闭循环，那就是，通过正对应从原来的集合出发，进入一个全新的像集合，然后可以通过逆对应，安全地回到原来出发的地方。
复平面是一种很特殊的结构。它与平面最大的不同是，实平面上的点与一对有序实数之间建立了一个一一对应，而复平面上的点是和一“族”终边相同的复数之间建立了一一对应。也正是由于这种特殊的结构，导致了复函数结构的复杂性，从而有了多值函数的概念。
如何处理多值函数，成为复变函数的一个核心内容。如何将一个多值函数单值化，在大学阶段的教科书中，多是采取缩小定义域的方法，或者说是将定义域分割成单值分值区域，成为复变函数理论中的特色内容[1] -[7] 。
缩小定义域，使得对应成为一对一的，这种思维方式是人们比较容易接受的一种方式。能否背其道而行，通过扩大定于域的方式实现一一对应？Riemann面的做法，给我们提供了一个典范。
本文就是试图用简单通俗的语言，以及生活中的一些直观的客观事物，来描述Riemann面的结构，从而从代数和几何两个方面去认识这个特殊的几何结构的特点及功能。进而了解数学中的几何概念与真实空间的几何体之间的相通之处和差别，为人们更好地认知事物，提供点滴帮助。
2. 从几何的角度看Riemann面
复多值函数的几何特征，就是像平面上出现了皱褶或者叠合这样的现象。单值化的核心工作，就是要把这些有皱褶或者叠合的地方，进行有效的“剥离”，从而使得平面是单层的，或者说，给了一个点，这个点只能出现在一个指定的平面上。
生活中有这样的实例，一张白纸上，我们可以复印字符，如果一张纸只往上复印一次信息，那么复印的东西清晰可见，如果往这张纸上反复复印字符，那么，尽管每一次复印的字符都是很明确的，但最终的结果，是纸面上一层层地叠满了字符，无法认出一个确定的点处乃至整个纸面上，到底印制的是什么东西了。但是，尽管我们无法用肉眼分辨出原来的东西是什么，信息都完整的保存于纸张上的。之所以认不出一个点出的字符串是由什么叠加起来的，是我们的眼睛不具有把它们剥离开来的功能。事实上，复印的过程是有序进行的，因此，只要在复印的过程中，将我们每一次在一个地方复印的信息做一个有效的记忆，或者给定一个有效的存储代码，那么纸张上复印的东西，就如同芯片上存储的信息一样，只要按照存储的规则提取信息，那么，纸张上的所有信息，都是有效可读的。也就是说，复杂结构上信息的有效提取，与提取的手段是息息相关的。
一个初等函数的Riemann面，是一个非常复杂的几何结构，我们甚至无法想象出它的结构复杂到什么样。但是，所有的Riemann面，都基于两种基本面：代数Riemann面；超越Riemann面。前者是一个有限层平面叠合在一起封闭系统，后者则是一个无限层叠合的开放系统。所谓封闭是指，当你在这个面上按照标识行走的时候，经过有限次重复旋转，就可以回到出发点。同样，开放则指的是，即使是按照指定的标识行走，也将永远无法回到出发点。
如果从几何的角度看代数Riemann面的话，它很像一座楼房的结构，楼梯连接着每一层直至楼的顶端，而电梯则一下把顶层和底层相连(假如电梯在中间的各层处没有出口)。这样一个设计于楼房中的交通通道，其功能和数学上的代数Riemann面是酷似的。不同的仅仅是表象。
上面的例子也告诉我们，实际上代数Riemann面的几何结构是平面上的立体空间结构。因为在代数Riemann面上确定一点的位置，必须知道三个量，一个是到原点的距离，一个是终边的具体位置，还有一个就是，终边停留的层数。在数学上，这个点需要用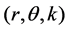
这样一个数组，才可以具体标明一个确定的点的具体方位。这恰恰是我们在三维空间中建立点与有序数组间一一对应所用的手法。
对于超越Riemann面，其几何结构与代数Riemann面在本质上是相同的，即：是一个平面上的立体结构。如果说有差别，那就是层数，一个是有限的，一个是无限的，而确定一个具体的点在Riemann面上具体位置的方法是相同的。
就一般的初等多值函数的Riemann面而言，其结构会很复杂，以至于我们都无法给出一个生活中的实例来描述其几何结构的形状。之所以这么复杂的原因归结起来大约主要有两个因素：其一，一个初等多值函数的单值分值区域可以是不唯一的。也就是说，同样的初等多值函数，同样的人，可以构造出完全不同的单值解析分值区域来。而且，这样的单值分值区域都是“合理”的。其二，得到了一个初等多值函数的单值分值区域后，如何将其“粘合”成为Riemann面，也和具体人的构造过程相关，没有统一的方法，所以构造出来的Riemann面也是不唯一的。因此说，一个初等多值函数可以有多个几何结构相差很大的Riemann面。
初等多值函数的Riemann面之所以复杂，还可以从初等函数的定义中看出端倪，因为初等函数生成方法中不仅仅包括由基本函数进行有限次四则运算这样的方式，也包括了用有限次复合运算这样的方式。于是，由于搭建初等函数的基本元素---基本初等多值函数，本身就已经是一个平面上的立体结构，由他们生成的初等函数可谓是“平面上立体中的立体”或者说，平面上“多重立体”镶嵌的“超立体”结构。而且，每一个基本初等函数构成的平面立体结构，独立地构成一个“王国”，通过其与整体函数的Riemann面的接口进出，实现与整体的交流。例如
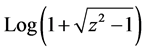
这样一个看似很简单的初等函数，其Riemann面的结构，就很复杂。究其原因，是由于这个函数本身是一个复合函数，外层函数的Riemann面是对数型的，有无限多层，内层函数的Riemann面是代数型的，有两层，这使得函数本身的Riemann面，将是一个由一个“两层”的“立体”的Riemann面，有效衔接到一个无限层“立体”的Riemann面的每一层上，并使得任何局部不能有所谓的几何上的皱褶，或者是代数上的多值(或重点)的现象发生的过程。可见，构造这样一个平面上的“天外有天”一样的结构，是多么的不易。而这样的结构却在真正的意义上做到了，面上有“体”，体中存“面”，而面中还可以藏“体”这样一个反复蕴藏，并秩序井然的几何结构。
这样的想法，看似难以实现，但是，生活中确有这样的应用。例如，前面我们列举的将高维的复杂数据有效地储存于计算机的芯片上，从而实现了数据结构的平面化的过程，就是这种思维模式的成功范例。
3. 从代数的角度看Riemann面
函数论研究过程中，有效的建立一一对应，是一个核心的问题。
通常建立一一对应，都是设法剔除掉那些破坏了一一对应规则的方式。而实现这样目标的方法，多是采用缩小定义域的模式来实现。这样的处理问题的方法，在中学中处理三角函数的反函数的时候，就有了很明确的表现。进而，对于周期函数的处理，都是按照这种模式，并结合周期内，函数的增减区间，加以实现的。
对于复变函数而言，由于定于域是一个全新的复杂的区域-复平面上的复数，已经不是一个几何点的位置上，仅仅只占有一个复数，而是占有一簇终边相同的复数。因此，对于复平面上建立函数这样的问题，必然会有所变动。例如，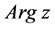
就是一个与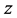
相伴相生的多值函数。也正是由于这个与
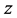相伴相生的函数
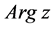与生俱来的多值性，导致了复变函数中，函数的概念里引入了一对多这样的对应关系。也就是说，多值函数成为一个不得不面对的既成事实。
由于多值函数的讨论，从根本上说，必须有效的化为单值函数来处理，这是一个必然的选择。这也就使得，多值函数的单值化问题，成为了复变函数研究的一个很具特色性的知识群，也是函数研究的一个难点问题。
复变函数的教课书中处理多值函数的方法，沿用了过去处理多对一这样的理念，也就是说，处理多对一，我们按照某种方法，将定义域进行有效的划分(通常最有效的方法，是利用单调性来处理)，使得每一个局部上，对应成为一对一的。教材中，陈述的如何构造出单值分值区域，并利用做割线的方法，把函数的定义域，分割成一个个小的单值分支区域，就是这种模式的具体实现。
然而，这样处理问题是有代价的。那就是：原有的完整的定义域(亦可是值域)，被人为的切割成了一片片的，多出了很多的裸露的、带有切割人主观意念的、而且可以是“随性而为”的边界线，以及对这些边界线上做有某种标示的人为的特殊解释。使得以前纯自然的状况，在某种程度上，受到了人为的“污染”或者“加工、处理”。
Riemann面的做法，与上面的思维方式可以说是截然不同的。其做法不是采用切割的办法缩小定义域去实现一一对应，而是想方设法，通过扩大定于域的办法，实现重叠数据的剥离。通过这样的方式，在Riemann面上，就实现了过去在实平面上具有的那种——有序实数与平面上的点之间的一一对应，这样的重要的特征。也就是说，Riemann面是一种在尽可能保持原貌的情况下，通过有效的重叠数之间的剥离，使得看似几何上完全相同的点，有了不同的标识，而在这样的标识下，实现了Riemann面上的点与复数之间一一对应。
需要说明的是，通过做割线缩小定义域的办法构造出单值解析分支来，相对比较容易一些，原则上只要是找到了初等函数的所有支点，并做一个通过了所有支点的曲线，作为割线，则所得到的区域，就是单值分支区域了。但构造Riemann面却要困难的多！事实上，构造一个初等函数的Riemann面，需要将一个个单值分支按照合理的方式，对区域中的多值部分，或者说过去平面区域上有“皱褶的”的部分，实现多值剥离后的粘合，而且这种粘合，要尽可能完整地保持原函数定义域在“几何”构成方面的‘原貌’，并使得剥离后通过粘合的方式得到的Riemann面上，标识明确，从而行走自如(前提是按照规则行进)，而且要达到原像与像之间的一一对应，很显然是一件很难做好的事情。
这就如同我们打碎一样东西相对容易些，而复原一样东西相对较难一样，如果复原还需要是在打碎的前提下，带有某种新功能的、有机的、再创造型的复原，那难度大是不言而喻的。
4. 随笔
Riemann面作为一种拓扑结构，为我们研究函数，提供了新的方式和研究范畴，这种通过扩大函数定义域来实现一个对应过程中，原像与像之间的一一对应的思维模式，无疑是具有开拓性的。
然而，Riemann面结构的复杂性，以及制作过程中的诸多不可预见性，及几何原形的在现实空间中的不可见属性，也多少影响了其在几何学中，直观性上的价值。
如果我们把多值函数单值化，看成是一个问题的正演过程的话，那么构造该函数的Riemann面，无疑是该过程的反过程，或逆问题。由于逆问题的处理，在相当程度上，依赖于正问题的结果或者实现程度，而我们这里的正问题本身就是一个比较复杂的、如何把一个函数单值化的问题。正问题本身也仅仅是一个在理论上解决的比较完整，而实际操作时却常常无迹可寻这样一种情况，自然，逆问题无法得到完美的结果，实属情理之中的事情。
基金项目
国家青年基金(11201043)。