1. 引言
近几年来，土地储备成为金融风险的关键环节，为了预测金融风险，需要对土地储备方案进行风险评估。我们考虑到土地储备风险有诸多方面，主要包括政策法规风险、经营风险、金融风险和投资决策风险等[1] [2] 。通过对土地储备项目可研性报告所给出的数据进行分析，我们发现影响投资决策风险的因素在数据中有较多体现。因此，本文主要针对投资决策风险展开研究。根据土地储备的自身经营特点构建土地储备投资决策风险评价指标体系，并通过计算出风险程度Q值作为观测风险大小的指标，从而对土地储备方案进行风险评估。
2. 影响投资决策风险的因素
针对文献[3] (土地储备方案的风险评估，附件二：土地储备方案数据)，本文首先通过对该数据进行分析研究，初步得到收购储备面积、财务净现值、动态回收周期、折现率、风险程度Q以及资产负债率等都可能影响土地储备风险，同时由已有数据可以计算出一些直接影响土地储备风险的因素。但各种影响因素土地储备风险的影响程度不尽相同，所以我们需要归纳出投资决策风险的诸多影响因素并尝试建立数学模型来确定投资决策风险中各个影响因素的权重，以指出造成项目风险较大的因素。
3. 投资决策风险程度的确定
在投资决策风险分析时，可以通过已知数据计算风险程度Q，当风险程度Q的值越大时，说明土地储备风险越大；反之风险越小。确定风险程度Q的步骤详见文献[4] 。
由原始数据可以看出，同一行的数据给出了收购储备面积、财务净现值等影响储备风险的因素，同时也给出了申报项目当年、第一年、第二年的净现金流量和折现净现金流量以及出让计划中第一年、第二年所占的比例(不同行之间表示不同征地，没有可比性，不做对比)。我们可以由此计算出期望、期望现值、标准离差和综合标准差，进一步计算出Q值，并对同一行第一、二年的Q值大小进行比较。通过计算可以看出，除第1、2、4个项目外，其他项目第一年的风险程度Q值均为0.95，而第二年的风险程度Q值在0.24到0.34之间，对比结果显示，同一行第二年的Q值小于第一年的。由文献[5] 我们得到：在正常情况下，土地的储备时间越长，土地储备风险应该越大，则风险程度Q的值也越大。此时，计算结果与实际发生了矛盾。我们分析发生这种情况的原因可能有：
(1) 大量土地闲置，收益少，导致土地储备风险变大；
(2) 住宅区、商业区及工业区在建设过程中没有带来利润，使得土地储备风险变大。
4. 投资风险评价指标分析
通过查阅大量文献及相关资料，最终确定收购储备面积、财务净现值、动态回收周期、折现率、风险程度Q以及资产负债率为投资决策风险的主要影响因素[2] [6] [7] [8] 。这些因素对风险的影响的趋势为：
(1) 收购储备面积：在不考虑其他因素变化的条件下，储备面积越大，风险越大；
(2) 财务净现值：财务净现值越大，风险越大；
(3) 动态回收周期：对同一收购土地，动态回收周期越长，其储备时间越长，风险越大；
(4) 折现率：折现率可以直接反映风险的大小，折现率越大，风险越大；
(
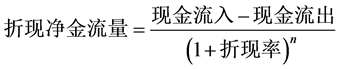，n为折现年数，由此计算折现率)
(5) 资产负债率：对于债权人来说，资产负债率越低，说明债权人拥有资金越多，负债较少，还债压力较小，因此风险相对较小；
(6) 风险程度Q值：Q值越大，说明土地储备风险越大；反之风险越小。
5. 投资决策风险评价指标权重的确定
5.1. 层次分析法确定权重
本文主要采取层次分析法确定上述六种指标对投资决策风险的权重，引用文献[2] 的结论，其具体步骤为：
(1) 确定出判断矩阵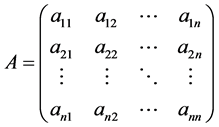
，并将A按列规范化：
；
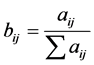(2) 将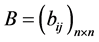
按行求和：
；
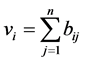(3) 规范化：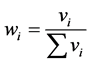
，得到权重向量：
；
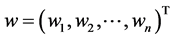(4) 计算判断矩阵的最大特征值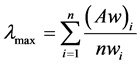
，其中
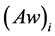为向量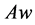
的第i个元素。
5.2. 一致性检验
根据Saaty引入的一致性指标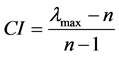
可知，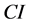
越大A的不一致性程度越高。
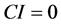时A为一致阵。
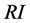为随机一致性指标。定义一致性指标为
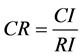，当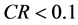
时认为A的不一致性程度在允许范围之内，可用其特征向量作为权向量。
求组合权向量：该指标的权重和相应准则层中指标权重的两两乘积之和[9] 。
5.3. 对传统层次分析法的改进及对数据的处理
传统的层次分析法在构造判断矩阵时采用美国运筹学家T.L. Saaty提出的1-9标度方法，该方法根据影响因素的重要性来确定判断矩阵A的元素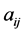
，这往往有一些主观因素，我们考虑运用一种相对客观的方法来确定判断矩阵。应用R型聚类分析，在对变量进行分类的同时，可以确定两个变量之间的相关系数。根据相似矩阵我们可以给出判断矩阵A的具体形式，而不是根据影响因素的重要性人为地给出相似矩阵。具体做法为：由于相关系数取值范围为
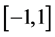，根据T.L. Saaty的1-9标度方法，判断矩阵A的元
素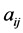
的取值为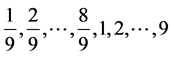
这17个数。我们不妨设
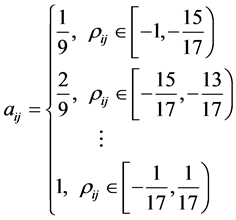
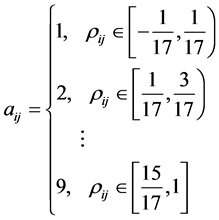
这样就可以得到判断矩阵A的具体形式。
这种方法避免了传统层次分析法确定判断矩阵A时的主观性，在1-9标度法的基础上具体求解出了判断矩阵，而不是根据经验或者专家评定来确定一个大致的取值范围。因此，该方法提高了层次分析法的效率。根据所给数据，应用SPSS进行聚类分析[10] ，得到如下相似矩阵(见表1)。
对该相似矩阵进行分析，不难发现以下几点：
(1) 相关系数最大值为0.266，相关性不大。由上述求A的方法，我们可以根据表1中相关系数的取值求解判断矩阵A，从而用层次分析法确定权重。
(2) 根据以上理论，利用C++编程实现求解，得到的判断矩阵为：
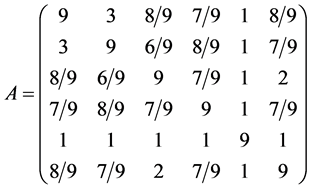
进而求得权重向量为：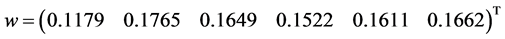
；
一致性指标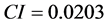
；
；
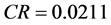组合权向量为：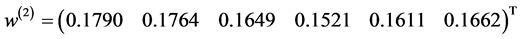
。
Table 1. Proximity matrix
表1. 相似矩阵
(3) 结果分析：
(a) 与其余因素相比，收购储备面积、财务净现值、动态回收周期、折现率、风险程度Q以及资产负债率这几类因素的权重较大，说明它们对投资风险的影响相对较大；
(b) 一致性指标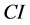
的值与0接近，说明A比较接近一致阵；
(c)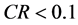
，说明A的不一致性程度在允许范围之内，可用其特征向量作为权向量。
6. 影响土地储备风险的其他因素
通过分析数据，由预期收益、总储备成本估算和收购储备面积，计算出不同规划用途的项目单位面积土地利润的均值，即
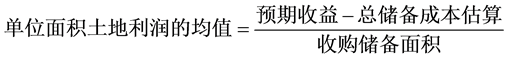
得到项目规划用途与利润关系统计表(表2)。
由表2可以看出，单位面积的土地投资工业用地，商业、住宅、综合用地，商业用地，综合用地，住宅用地，商业、住宅用地的利润均值依次增大，从而对投资决策风险的影响程度也依次增大。例如，商业、住宅用地对投资决策风险的影响程度最大，这是符合常识的。随着经济的发展，商业用地越来越多，商人竞争激烈且商品房房价相对较高，一些商业用地造成闲置。同时，商业区比较繁华，该区居民住宅房价较高，开发商会尽可能多地在该区建设住宅房，然而由于房价的不断飘升，住宅用地也会造成一定的闲置，这很大程度上增大了投资决策风险。
7. 敏感性分析
利用Yaahp软件对结果进行敏感性分析，在该软件的权重设定区域中，当改变某个影响因素(例如财务净现值)的权重时，备选土地序号对风险影响的权重将随之改变。通过该软件分别改变六种影响因素的权重，发现当各个变量变化不大时，组合权向量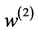
变化也不太大。故可以根据权重w评估投资决策风险。
8. 结论
根据层次分析法确定的权重w评估投资决策风险，最终得到各因素对投资决策风险的影响程度由大到小依次为：风险程度Q，折现率，收购储备面积，资产负债率财务净现值，动态回收周期。因而为土地储备部门提供一个土地储备方案的风险评估方法。
9. 模型评价
9.1. 优点分析
本文主要采取层次分析法确定影响指标对投资决策风险的权重，在T.L. Saaty提出的1-9标度法的基础上做了改进，利用SPSS (R型)聚类分析过程中的相似矩阵来求解判断矩阵。这种方法避免了1-9标度方法带来的主观因素，提高了层次分析法的效率。
9.2. 缺点分析
本文主要侧重分析六种因素对投资风险的影响，并没有具体给出其他因素对其影响相对不大的原因，这是本文的一个疏漏之处。
另外，本文在通过Yaahp对结果进行敏感性分析时，只是具体替换了一些数据，发现当各个因素变
Table 2. Statistics of the relationship between project planning purposes and profit
表2. 项目规划用途与利润关系统计表
化不大时，组合权向量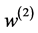
变化也不太大。因而决定权重w可以作为评估投资决策风险的指标。这在某种程度上是不太严谨的。
致 谢
本文的完成过程中得到了内蒙古大学数学科学学院刘洋副教授许多好的建议和意见，在此对刘洋副教授表示衷心的感谢!
基金项目
国家大学生创新训练项目(201310126040)，内蒙古大学大学生创新训练项目(201311140)。