1. 引言
卫星导航系统在人类社会经济生活和各国军事国防中占据着至关重要的地位。然而,卫星导航系统往往会受到多种形式的有意或者无意干扰,导致导航定位性能下降,甚至无法工作。对于卫星导航系统接收机主要有两种干扰样式:压制式干扰和欺骗式干扰。欺骗式干扰是发射与导航信号相类似的干扰信号,误导卫星导航接收机偏离准确的导航和定位,这种干扰所需的功率小,干扰效率优于压制式干扰[1] 。卫星导航系统接收机如何抗欺骗干扰已经成为当前迫切需要解决的科学问题。
抗欺骗干扰的前提是接收机能够检测识别出欺骗干扰。目前国内外针对欺骗干扰识别方法的研究主要集中在基于特征提取的干扰识别算法,所提取的特征参数包括时钟偏移、多普勒频移、和接收机位置等[2] -[5] 。但这些研究仅考虑了信号波形间整体的差异而忽略了欺骗干扰与真实信号间某个或多个信号参数上的细微特征,而且基于的信号的模型较简单。所以,针对基于细微特征参数差异上的欺骗干扰检测识别问题,进一步深入开展研究基于统计信号检测识别理论的新方法是很有必要的。近年来,研究人员发现即使是同一条生产线制造出来的同一批次的射频元器件也存在着细微差异[6] 。这些细微差异使得输出信号附加上了不影响信息传输的“指纹”特征,这一类“指纹”特征的提取已成为研究热点之一[7] 。然而,这些提取“指纹”特征的方法多是通过信号分析手段,寻找的依然是信号在时域、频域或时频域的特征参数,识别效果不够理想。
本文针对产生式欺骗干扰检测问题开展研究,通过深入剖析干扰机射频前端元器件的工作机理,从射频元器件非线性建模角度出发,在假定干扰机射频前端除DAC外其余射频元器件均工作在理想状态的条件下,推导出DAC的统计建模。在此基础上,提出了似然比干扰检测法与欧式距离干扰检测法。理论分析与仿真表明,所提出的模型与方法能够基于信号的微小差异而实施较为准确的检测。
2. DAC的统计建模
DAC的编码主要有三种方式:分段编码、二进制编码和温度计编码。对于这三种主要编码方式的DAC的饱和区电流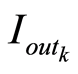 ,一般来说,可以由单位电流
,一般来说,可以由单位电流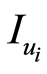 总和得到。分段编码DAC的饱和区电流
总和得到。分段编码DAC的饱和区电流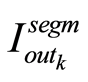 可以由式得到,其中
可以由式得到,其中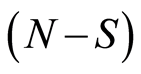 位LSBs是以二进制编码方式编码,而
位LSBs是以二进制编码方式编码,而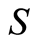 位MSBs是由温度计式编码方式编码,则有
位MSBs是由温度计式编码方式编码,则有
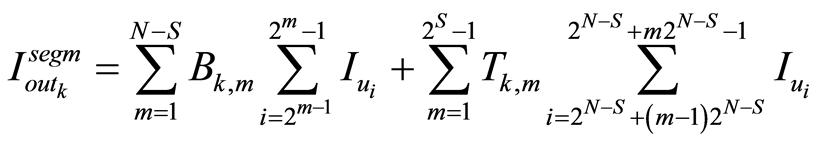 (1)
(1)
式中,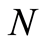 是DAC的位数,
是DAC的位数,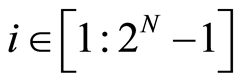 ,
,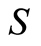 表示由温度计编码的位数,
表示由温度计编码的位数,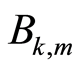 和
和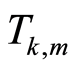 分别表示二进制编码和温度计编码部分的转换矩阵。
分别表示二进制编码和温度计编码部分的转换矩阵。
最能描述DAC非线性特征的参数是积分非线性误差(INL)和微分非线性误差(DNL)。根据IEEE对INL[8] 的定义,它描述的是除去失调误差和增益误差后,DAC的输出曲线与理想曲线间的偏差,其计算公式为
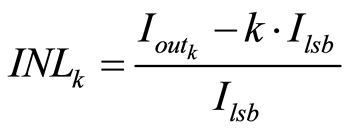 (2)
(2)
式中,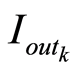 表示输入码为
表示输入码为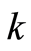 的DAC输出电流,
的DAC输出电流,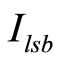 表示最低有效位输出,可表示为
表示最低有效位输出,可表示为
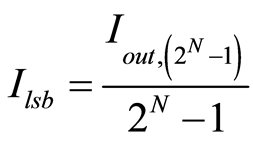 (3)
(3)
对于温度计编码的DAC来说,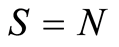 ,式中
,式中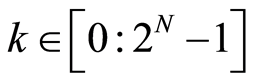 ,
,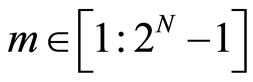 ,那么
,那么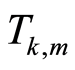 可以表示成
可以表示成
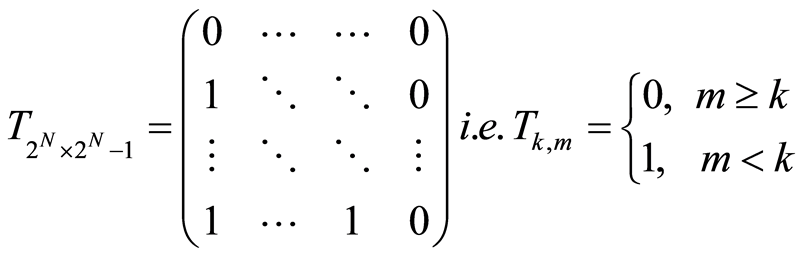 (4)
(4)
所以,式可以简化为
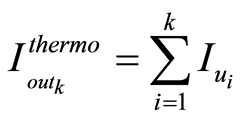 (5)
(5)
式中,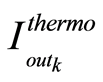 表示以温度计式进行编码的DAC的饱和区的电流。
表示以温度计式进行编码的DAC的饱和区的电流。
那么,累积的失配误差可以表示成
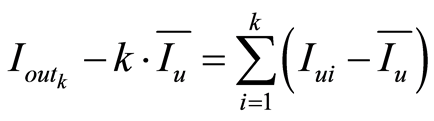 (6)
(6)
式中,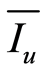 是理论上的单位电流源。这一偏差可以建模为维纳过程[9] ,即有
是理论上的单位电流源。这一偏差可以建模为维纳过程[9] ,即有
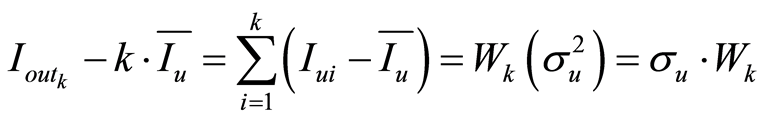 (7)
(7)
式中,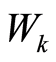 是一个维纳随机过程且具有以下的性质
是一个维纳随机过程且具有以下的性质
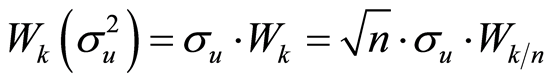 (8)
(8)
式中,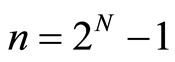 。
。
这样,式(2)的分子项为
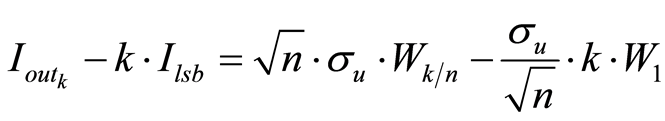 (9)
(9)
根据布朗桥过程的定义[9] ,上式可以改写成:
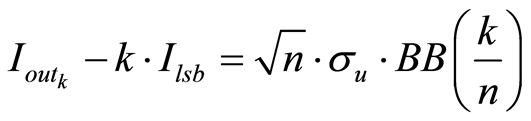 (10)
(10)
所以,INL可以表示为:
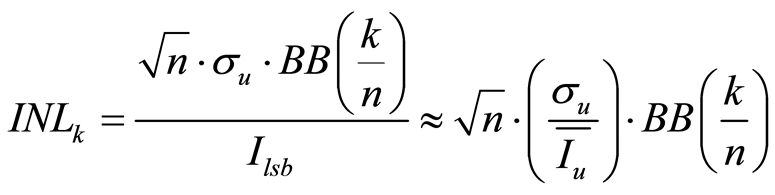 (11)
(11)
根据定义[8] ,DNL(微分非线性)的数学表达式为:
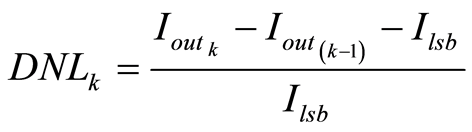 (12)
(12)
利用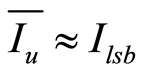 这一关系[10] ,且根据
这一关系[10] ,且根据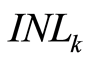 的定义,可以推导出
的定义,可以推导出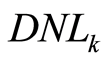 与
与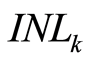 的关系,即:
的关系,即:
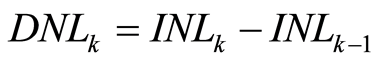 (13)
(13)
由已知的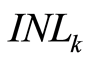 的数学模型,易推导出
的数学模型,易推导出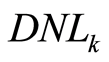 的数学模型,为:
的数学模型,为:
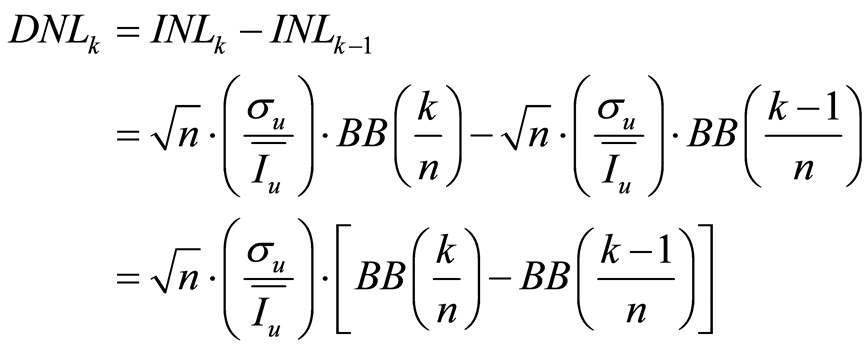 (14)
(14)
文献[11] 给出了布朗桥随机过程的K-L展开为
 (15)
(15)
其中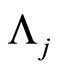 是独立同分布的随机变量,服从
是独立同分布的随机变量,服从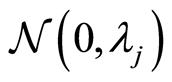 。
。
实际中,设输入信号为x,且长度为M,即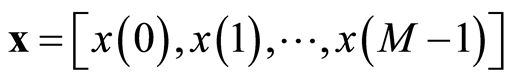 ,则离散布朗桥过程
,则离散布朗桥过程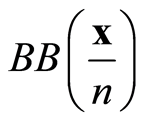 可以表示为
可以表示为
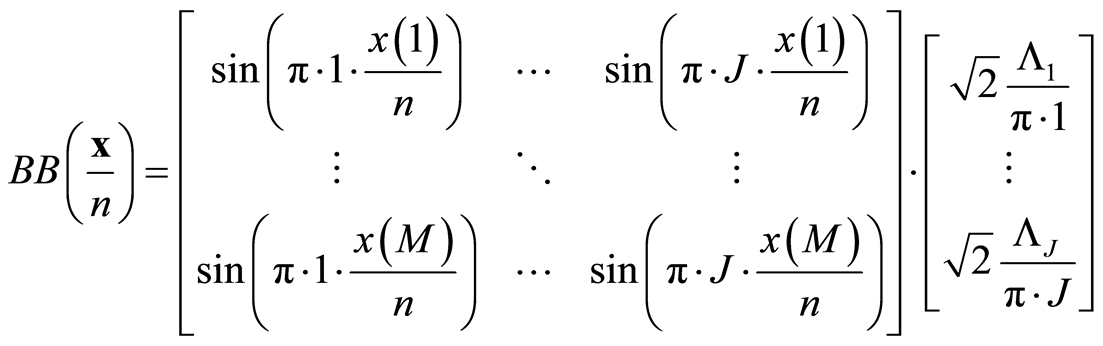 (16)
(16)
这样,式(12)可写为
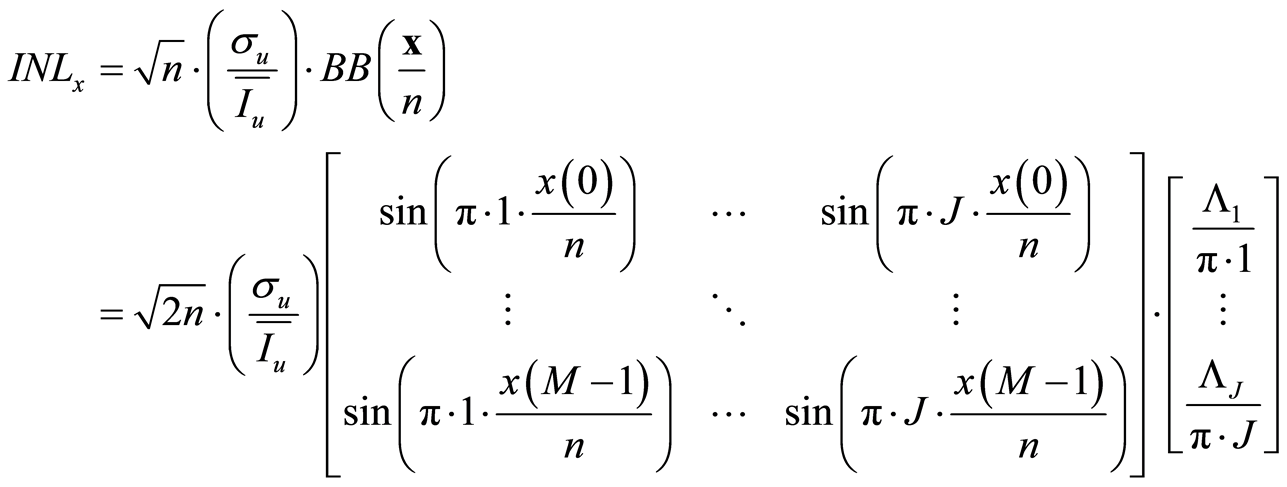 (17)
(17)
分别令
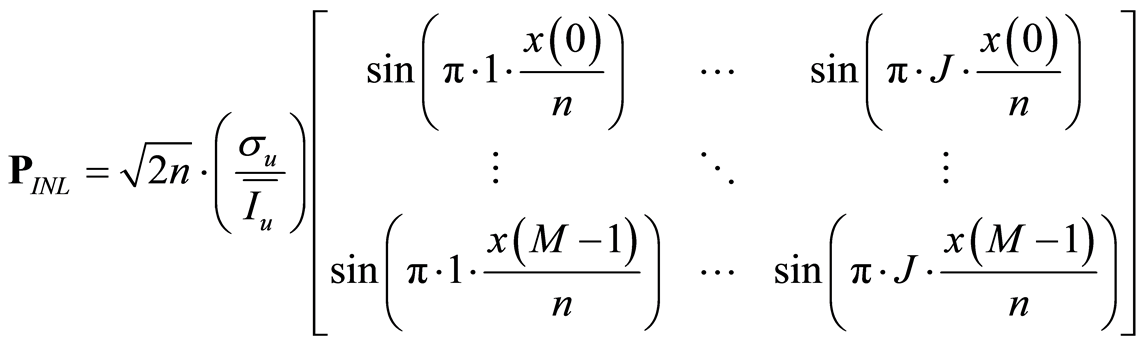 (18)
(18)
和
 (19)
(19)
则式(17)可以简单地表示为
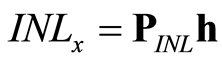 (20)
(20)
同理,根据式(15),DNL可以表示为
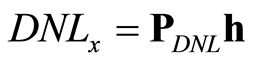 (21)
(21)
式中,
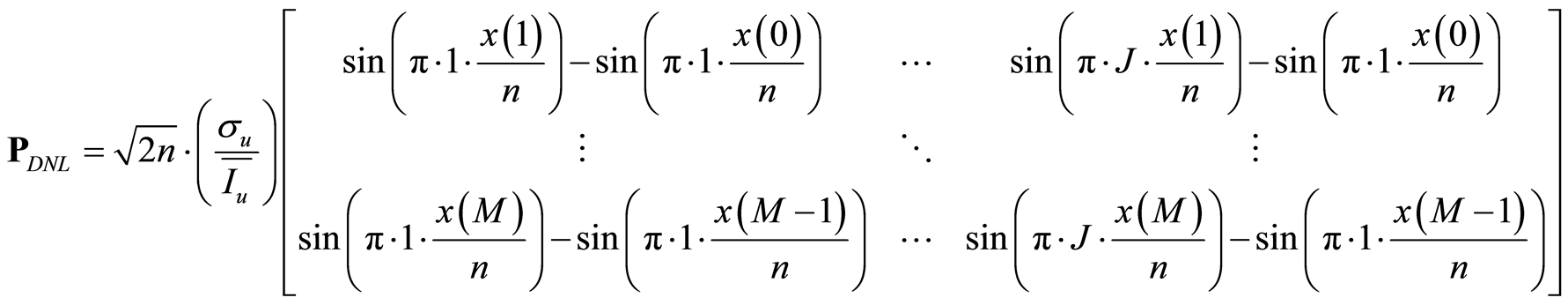
3. 检测算法
根据式(21)或式(22),接收机接收到的分别由真实发射机和欺骗干扰机发射的信号可建模为
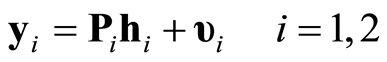 (23)
(23)
其中,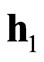 与
与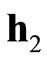 分别为由式(20)表示的真实发射机和欺骗干扰机的模型参数向量;
分别为由式(20)表示的真实发射机和欺骗干扰机的模型参数向量;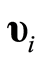 设为服从均值为0、方差为
设为服从均值为0、方差为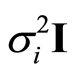 的高斯分布噪声向量;当以INL作为检测参数时,
的高斯分布噪声向量;当以INL作为检测参数时,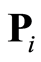 为由式(18)表示的DAC输入矩阵;当以DNL为检测参数时,
为由式(18)表示的DAC输入矩阵;当以DNL为检测参数时,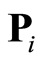 为由式(22)表示的DAC输入矩阵。
为由式(22)表示的DAC输入矩阵。
接收机根据接收信号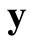 ,判别是否受到欺骗干扰。基于上述模型,欺骗干扰的检测问题为
,判别是否受到欺骗干扰。基于上述模型,欺骗干扰的检测问题为
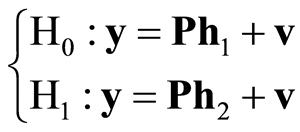 (24)
(24)
式中,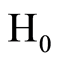 表示接收机接收的信号为真实的信号,
表示接收机接收的信号为真实的信号,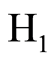 表示为接收机接收的为欺骗信号。基于该模型,拟采取以下两种检测算法。
表示为接收机接收的为欺骗信号。基于该模型,拟采取以下两种检测算法。
3.1. 似然比检测法
1) 判定函数
假定模型参数向量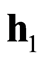 与
与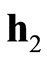 已经提取得到,则似然比函数为
已经提取得到,则似然比函数为
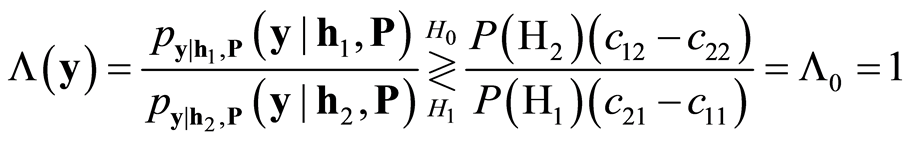
 (25)
(25)
式中,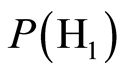 、
、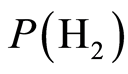 表示两种情况出现的概率,这里假设相等,
表示两种情况出现的概率,这里假设相等,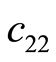 、
、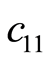 为正确判断的代价,为0,
为正确判断的代价,为0,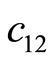 、
、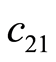 为错误判断的代价,为1,故
为错误判断的代价,为1,故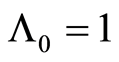 ;
;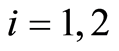
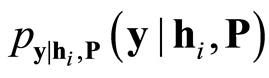 是条件概率密度函数,其表达式为
是条件概率密度函数,其表达式为
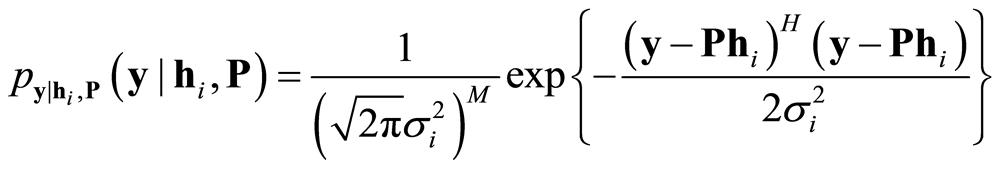 (26)
(26)
则判决函数可以简化为
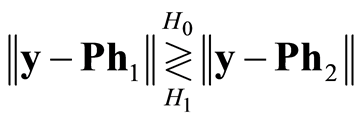 (27)
(27)
2) 性能分析
检测错误概率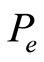 为
为
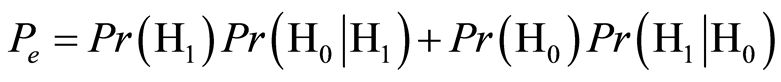 (28)
(28)
其中,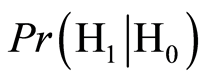 是接收机实际接收到的是真实信号,而被判决为欺骗信号的概率;
是接收机实际接收到的是真实信号,而被判决为欺骗信号的概率;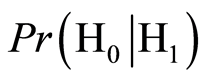 是接收机实际接收到的是欺骗干扰信号,而被判决为真实信号的概率。
是接收机实际接收到的是欺骗干扰信号,而被判决为真实信号的概率。
假设接收机等概率地接收真实信号和欺骗干扰信号,则有
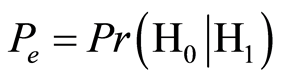 (29)
(29)
结合式(28)和式(30)可得
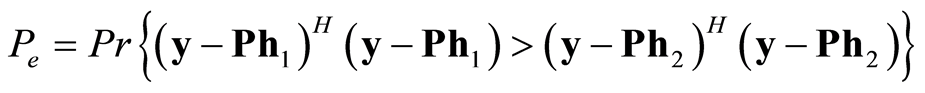 (30)
(30)
由于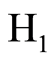 假设条件下,
假设条件下,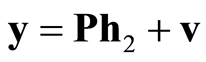 ,则式(31)可化简得
,则式(31)可化简得
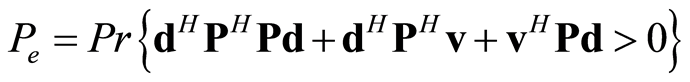 (31)
(31)
其中,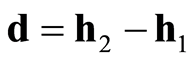 。
。
3.2. 欧式距离检测法
还有一种较为直观的检测方法是比较接收信号的特征向量与已知特征向量间的欧式距离大小,判决准则为
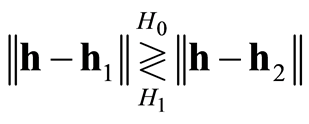 (32)
(32)
4. 仿真验证
4.1. INL和DNL
设定DAC位数为14位,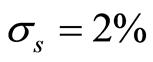 ,
,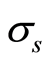 为DAC的内部电源方差均值比。经仿真,所得到的INL和DNL分别如图1和图2所示。图1是14bitDAC100条输入编码的INL的matlab仿真图;图2是14bitDAC100条输入编码的DNL的matlab仿真图。
为DAC的内部电源方差均值比。经仿真,所得到的INL和DNL分别如图1和图2所示。图1是14bitDAC100条输入编码的INL的matlab仿真图;图2是14bitDAC100条输入编码的DNL的matlab仿真图。
4.2. 基于INL的欺骗干扰检测
真实信号和欺骗干扰基于信号锥[12] 产生,假定信号锥的大小为10度且信号锥内的信号均为真实信号。先根据式(21)仿真产生一个信号,并设定这个信号为真实信号;再在这个信号的基础上旋转15度,由于该角度大于信号锥大小,可认为属于欺骗干扰。另外,设定式(16)中的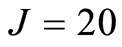 。
。
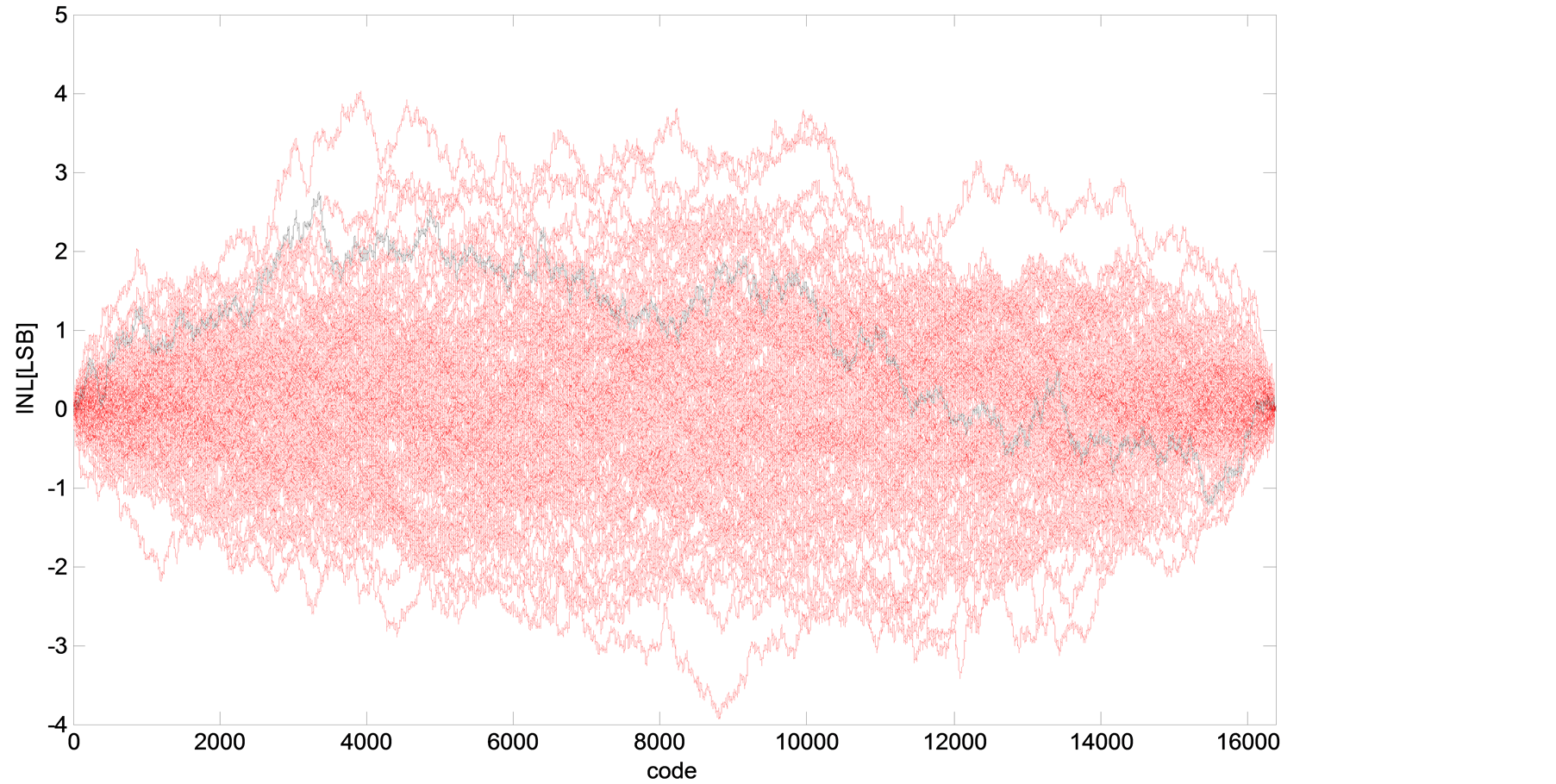
Figure 1. INL Brownian Bridge paths
图1. INL仿真图
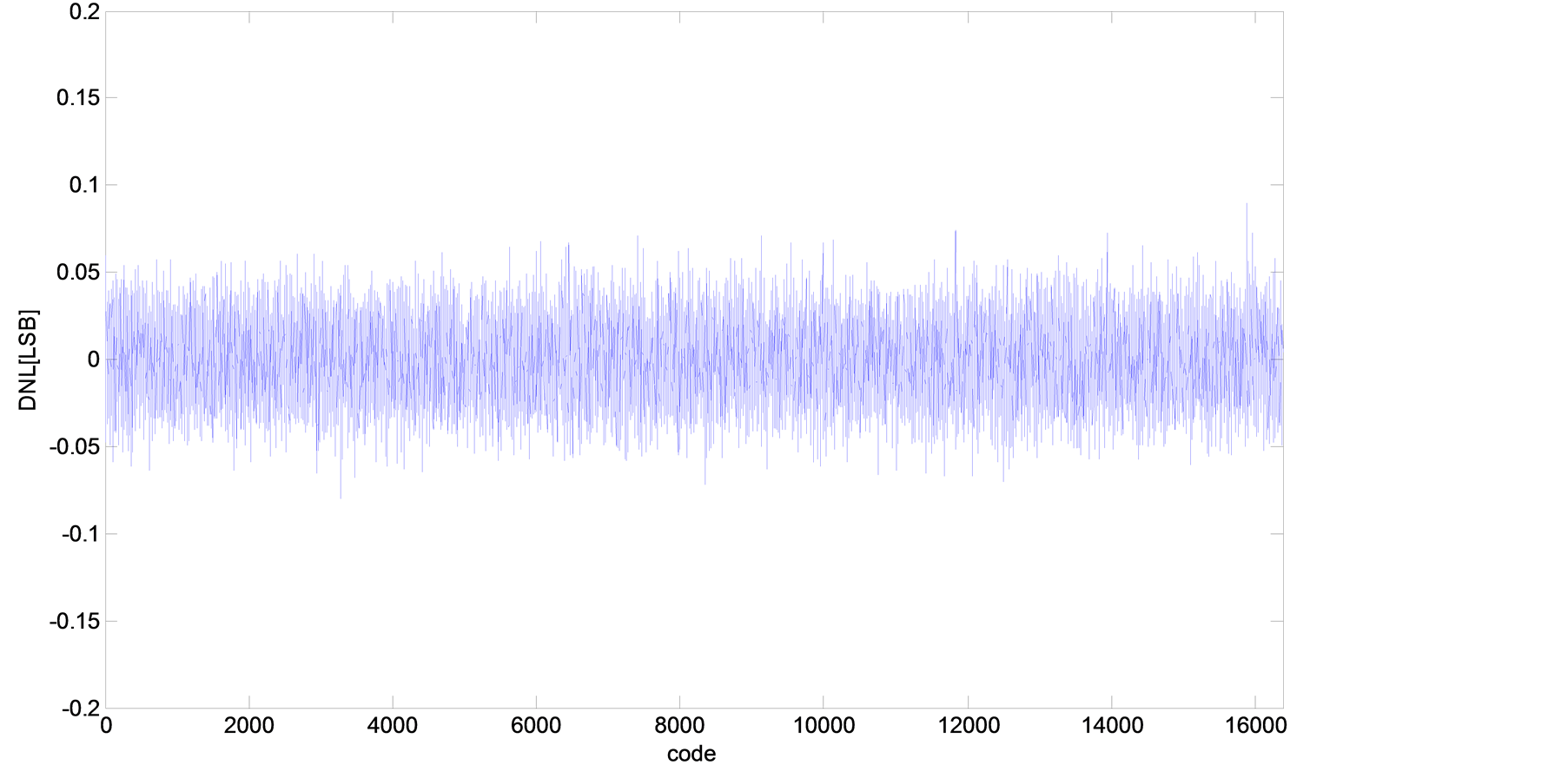
Figure 2. DNL Brownian Bridge paths
图2. DNL仿真图
首先比较两种检测方法的性能。实际中,一般的商业卫星导航系统采用的DAC的位数为1位,较高端的为1.5位或3位,极高端的为8位或以上。以下仿真假定DAC位数为3位。两种方法的性能比较如图3所示。
从图3可以看出,似然比检测算法的性能大大好于欧式距离检测法。随着SNR的增加,检测错误概率呈下降趋势,但似然比检测算法在SNR大于35 dB后错误概率趋于零,而欧式距离检测法的最终错误概率趋于25%。
另外,为了分析DAC位数对检测性能的影响,分别设DAC的位数为N = 1、N = 3位和N = 4,得到的检测性能如图4所示。图4表明,DAC位数为4位时性能最优,其次为3位和1位。
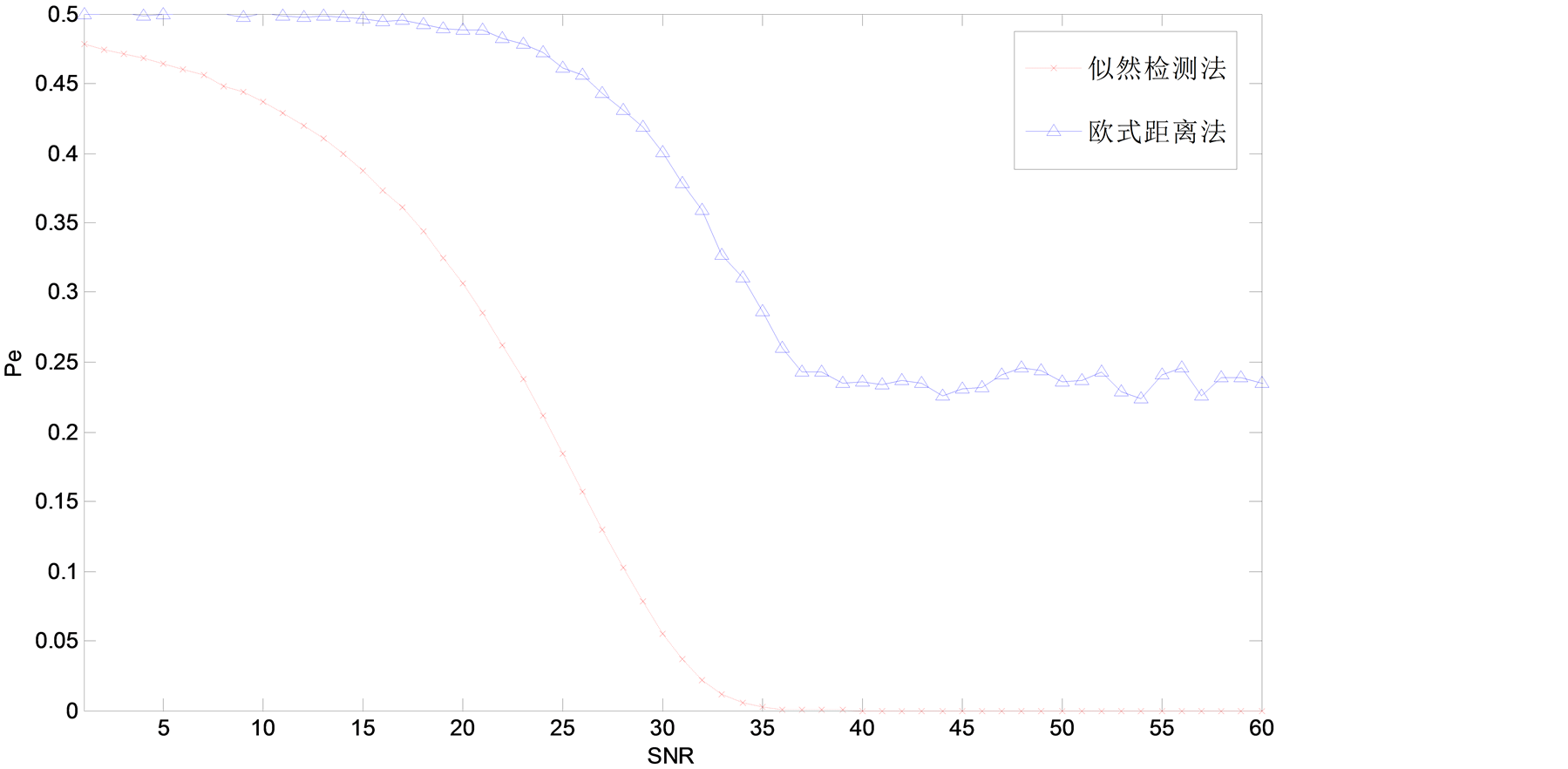
Figure 3. Probability of error vs. SNR of INL
图3. INL检测性能
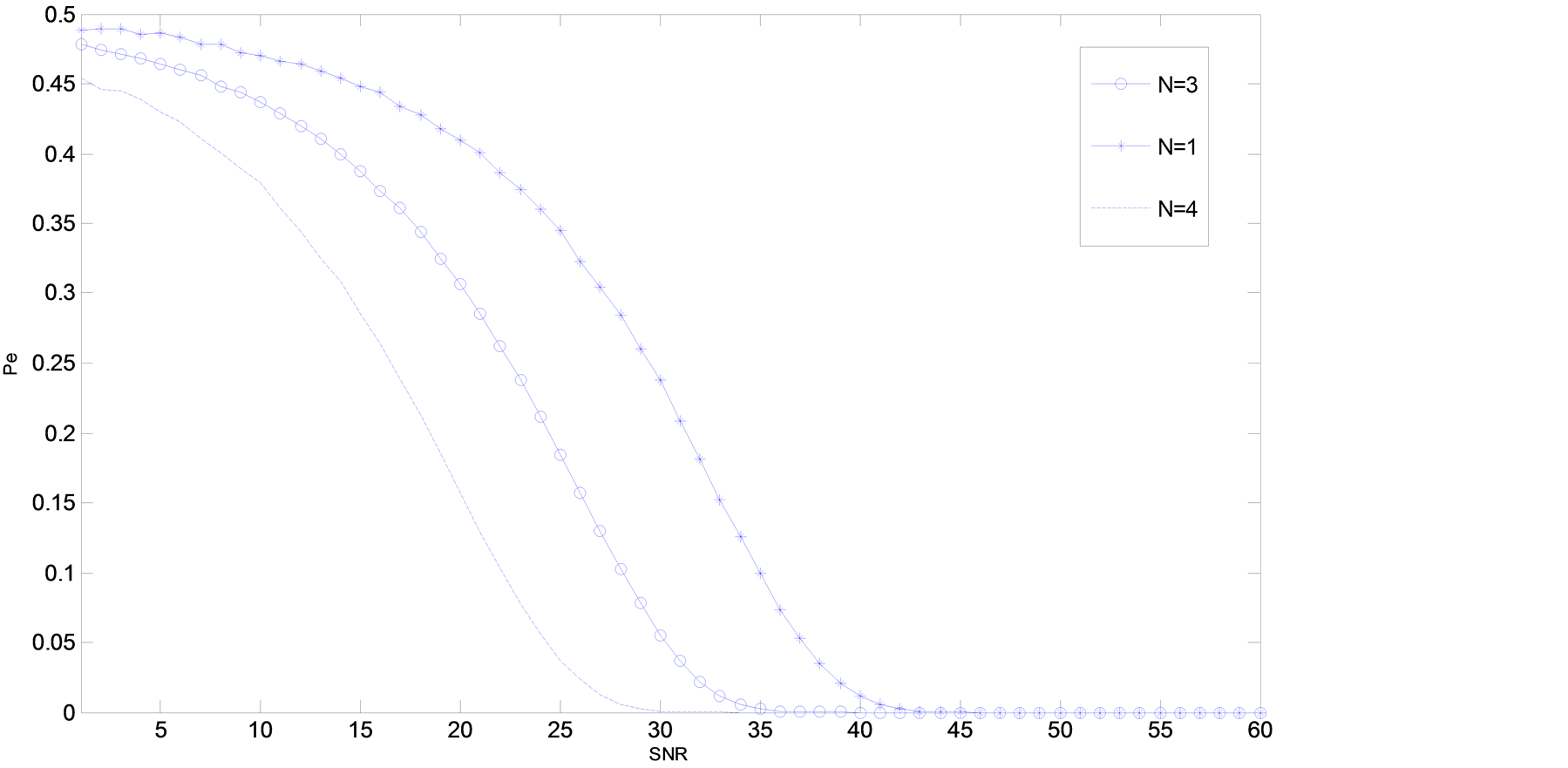
Figure 4. Probability of error vs. revolution of DAC
图4. DAC的位数对性能的影响
4.3. 基于DNL的欺骗干扰检测
DAC的非线性特征除了INL以外,还有DNL。图5给出了以DNL为特征向量,分别利用似然比检测法和欧式距离法进行的欺骗干扰检测性能曲线。
图5与图3类似,似然检测法的性能明显好于欧式距离检测法的性能。欧式距离检测法的错误概率最后收敛于25%左右,而似然比检测法在SNR大于30 dB后错误概率趋于0。
图6给出了分别以INL和DNL作为特征向量进行似然比检测得到的检测性能曲线。从图中可以看出,两者的检测错误概率均呈单调下降趋势,最后都能收敛于0;但DNL的下降速度要快于INL,图中可看出DNL检测性能优于INL检测5~7 dB。
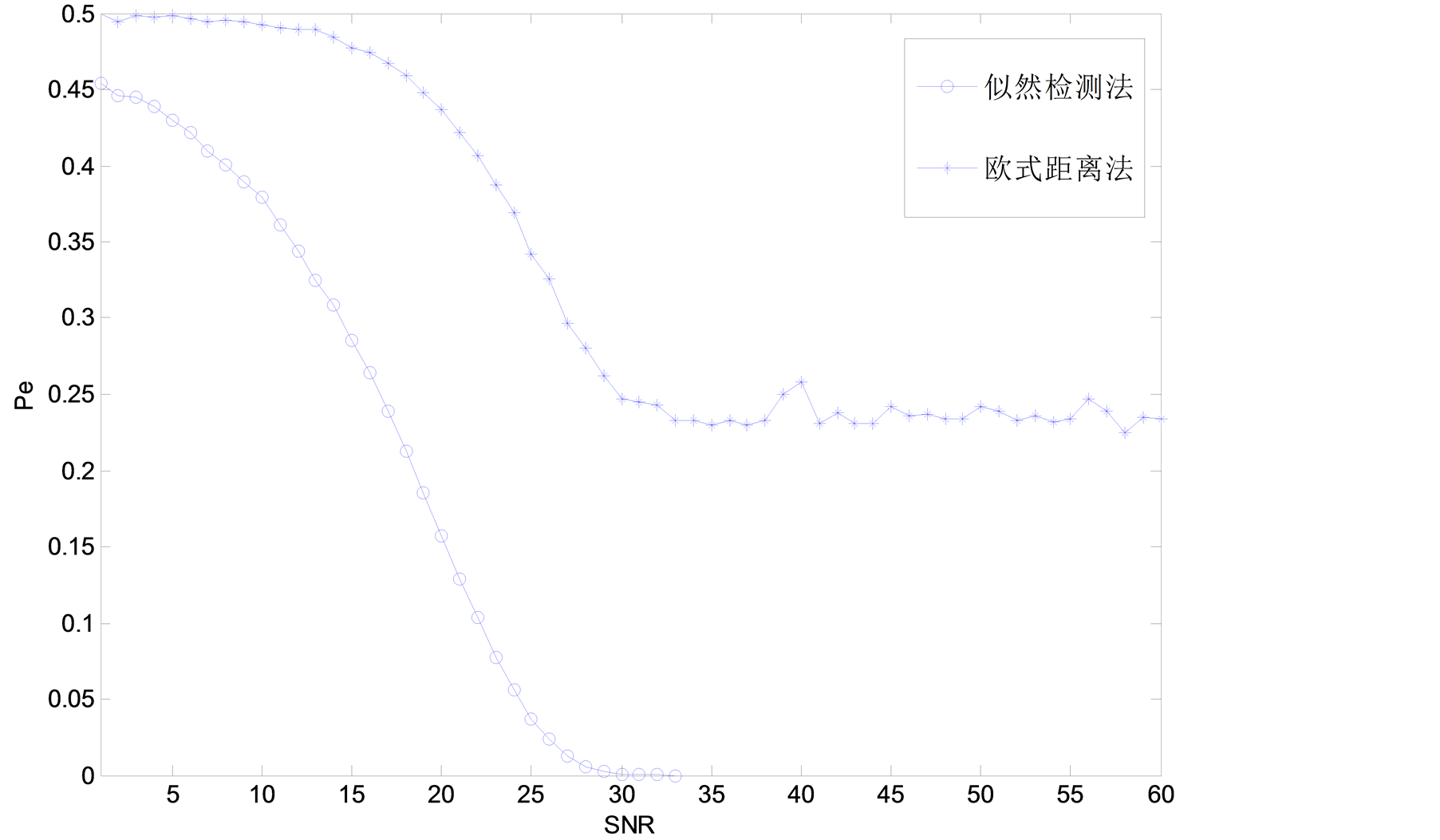
Figure 5. Probability of likelihood ratio test vs. naïve method of DNL
图5. 以DNL为特征向量的的两种检测法的比较
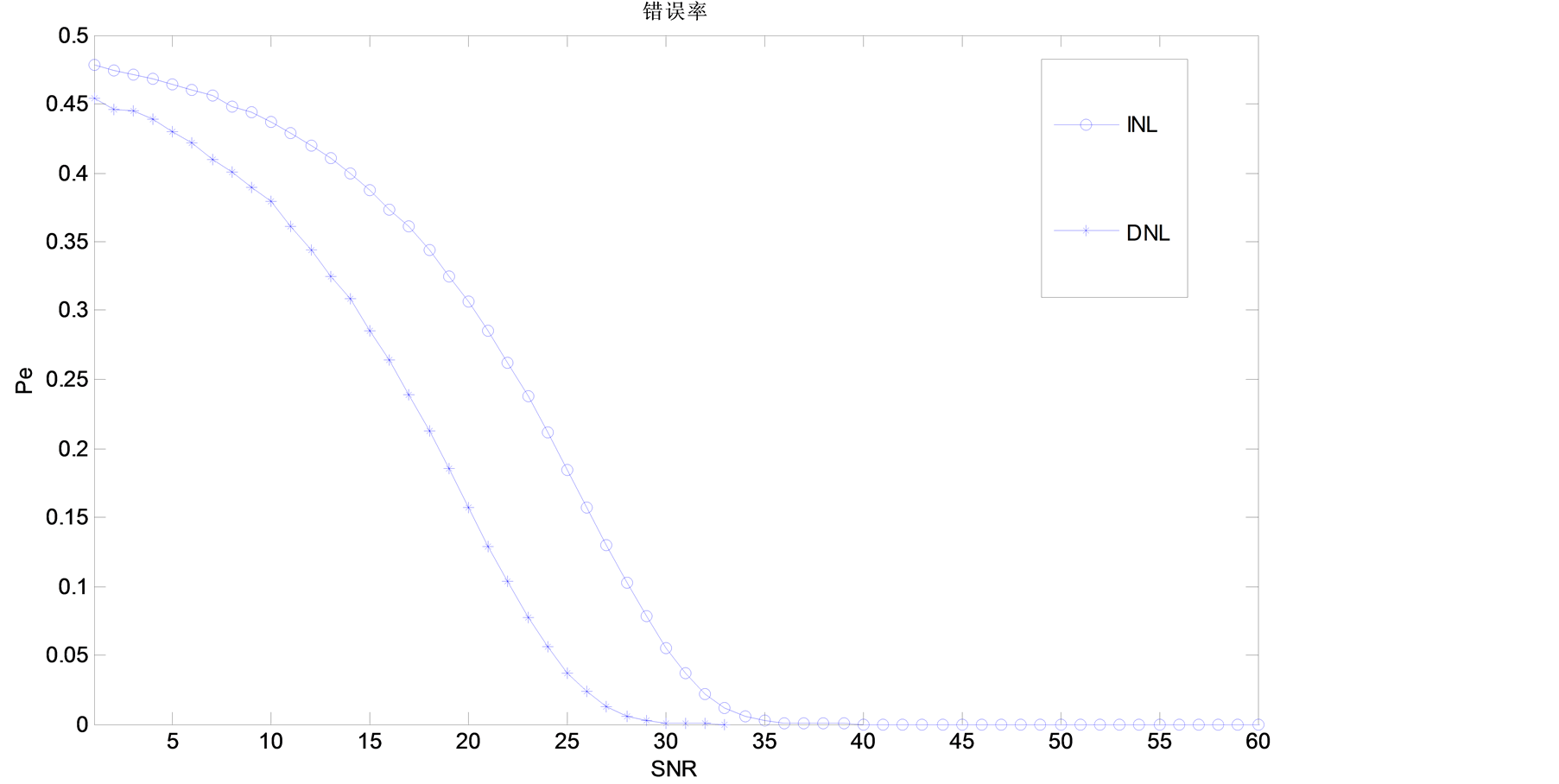
Figure 6. Probability of likelihood ratio test of INL vs. DNL
图6. INL与DNL似然比检测性能比较
5. 总结
由于实际生产中工艺的限制,DAC存在着内在固有的积分非线性误差和微分非线性误差,这些非线性的特征使每个DAC都具有自己的独特性,因此可以将这些非线性特征作为器件的“指纹”。本文首先从产生式干扰机的硬件结构出发,假设干扰机射频前端除DAC外均工作在理想状态,提出了基于DAC统计模型的欺骗干扰识别方法。分别利用INL和DNL两个非线性特征,提取了特征向量作为“指纹”特征。其次,利用似然检测法和欧式距离法,基于上述的特征向量,进行欺骗干扰检测。最后仿真结果表明,似然检测法和欧式距离法均能识别欺骗干扰,但似然检测法的性能要优于欧式距离法;并且,DAC的位数越高,对欺骗干扰的检测性能越好;另外,DNL的检测性能优于INL检测5~7 dB。
根据本论文所推导出的DAC的统计数学模型,并以此作为干扰检测的参数,利用似然检测方法与欧式距离法进行理论分析和实验仿真,结果表明,所提出的方法可以从较细微的差异中较为准确地进行干扰的识别。
致 谢
感谢国家自然科学基金资助项目(61271214)、浙江省教育厅资助项目(Y201121089)。