1. 引言
能源是人类生存和发展的重要物质保障,随着经济的高速发展,社会的快速进步以及人们生活水平的不断提高,中国能源消耗量在不断的增加,人类对能源的需求量也大幅度的增加,从而导致能源供给日趋紧张,能源问题也将成为我国未来经济发展和社会进步的制约因素。能源在国民经济中占有重要的地位,做好能源预测的相关工作,准确预测能源未来消费的发展趋势,可以给有关部门制定科学的能源战略规划,合理的能源消费政策提供依据,同时有利于维护我国国民经济健康、持续、稳定的发展,建设节约型和谐社会,这具有非常重要的现实意义和战略意义。
国内外很多学者采用不同的预测方法对我国能源消费总量进行研究,当然不同的方法其预测精度也不同。国外学者[1] [2] 分别建立ARIMA模型和GM(1,1)进行预测。国内学者如韩君[3] 运用趋势外推中的三次曲线模型对我国1990~2003年能源消费总量进行预测;程静[4] 以广东省1979~2006年能源消费总量为基础,运用Eviews软件,建立ARMA模型预测广东省2007~2010年的能源消费总量;徐明德[5] 采用灰色预测法进行预测分析;孙文生[6] 使用BP人工神经网络法预测河南省煤炭消费总量。目前,组合模型预测法备受欢迎,如柴元春[7] 以我国1989~2009年能源生产总量数据为基础,建立组合模型并证明其预测效果比单一模型要好;王惠婷[8] 将趋势外推模型与ARIMA模型组合,对河南省许昌市粮食产量进行预测,发现混合模型预测占优势;韩君也采用趋势外推与ARIMA组合模型分析预测了我国能源需求情况。
目前,云南省能源消费量相关预测的研究很少,基于能源对人类的重要性以及云南省是一个能源大省的事实,做好云南省未来能源消费总量预测工作意义重大,可以为云南省政府制定合理的能源战略及规划提供科学依据,保障云南省能源的合理利用以及健康稳定的发展。本文在一些学者研究的基础上,建立了混合时间序列模型进行预测分析,该模型弥补了单一趋势外推模型不能解释非趋势分量的缺陷,而且预测效果优于趋势外推模型。
2. 模型及方法
通过阅读大量的文献,我们了解到国内外学者对能源预测模型进行了大量的研究,目前主要的预测方法有趋势外推法、时间序列分析法、人工神经网络模型法、灰色预测法、能源弹性系数法、投入产出法和组合模型预测等方法。对同一数据使用不同的方法建立模型,得到的预测结果会存在一定的差异,它们的预测精度也各不相同。本文基于所选数据的特征,选择建立趋势外推模型和混合时间序列模型对云南省能源消费总量进行分析预测。
2.1. 趋势外推模型
2.1.1. 趋势外推法基本介绍
趋势外推法[9] ,又称趋势外插法,是根据过去和现在的发展趋势推断未来的一类方法的总称。其基本依据是预测的连续性原理,根据预测对象发展具有规律性的特点,通过正确把握预测对象过去和现在的发展状况,来预测未来的发展趋势。
随着时间的变化,事物的发展呈现一定的规律性,而且所要预测的对象也会具有一定的趋势,这时我们可以寻找合适的函数曲线来反映这种变化趋势,以时间 为自变量,时间序列值
为自变量,时间序列值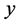 为因变量,建立趋势外推模型:
为因变量,建立趋势外推模型:
 (1)
(1)
而以顺延的时间作为已知条件,根据拟合的模型可以得到趋势值即预测值。由此看来,模型拟合的好坏将直接影响到预测的准确程度,我们常用最小二乘法拟合趋势模型,因为它拟合出的模型的预测标准误差最小。
2.1.2. 趋势外推模型的识别与选择
预测结果的准确与否与所建立的趋势模型有关,因此,曲线模型的选择至关重要,下面给出几种常见曲线模型的识别与选择方法:
1) 直观判断法。绘制已知时间序列数据的散点或趋势图,与常见的曲线模型比较,选择分布比较接近的曲线模型作为趋势外推模型。
2) 特征分析法。通过分析已知数据所具有的特征,从我们所熟悉的曲线模型中选择出与此特征相符的模型。
3) 预测精度比较法。当我们不能确定究竟选择哪一种模型来拟合历史数据时,我们可以把所有可能的曲线模型都分别来拟合一次,然后比较这几种模型的拟合优度,从而选择出最好的预测模型。
2.1.3. 曲线模型估计的步骤
当我们在解决实际问题时,不能确定哪一种曲线最能反映该问题的趋势情况,这时我们可以运用曲线估计。在估计过程中有很多曲线可供我们选择,如:线性、二次、三次、指数、增长等曲线,只要这些曲线可以描述变量之间的大概关系,我们就可以进行曲线估计分析。分析步骤如下:
1) 绘制已知时间序列数据的趋势图;
2) 根据趋势图,选择几种可能的曲线模型进行拟合;
3) 采用最小二乘法得到曲线模型的参数估计值,以及统计量R方、F值和P值;
4) 对参数估计的相关统计量进行检验,看其是否通过显著性检验;
5) 通常选择R方较大的模型作为预测模型,当然也可以进一步比较它们的预测精度进行模型筛选。
2.2. 时间序列分析法
时间序列分析法是以预测对象时间序列的历史数据为基础,运用一定的数学方法使其向外延伸,并对未来的发展变化趋势进行预测。
2.2.1. ARIMA模型基本介绍
ARIMA模型的全称为差分自回归移动平均模型,是由博克思(Box)和詹金斯(Jenkins)于70年代初提出的著名时间序列预测方法,所以又称为Box-Jenkins模型、博克思–詹金斯法。所谓ARIMA模型,是指将非平稳时间序列转化为平稳时间序列,然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。其基本思想是:将预测对象随时间推移而形成的数据序列视为一个随机序列,用一定的数学模型来近似描述这个序列。
ARIMA模型的结构[10] 为:
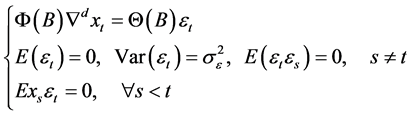 (2)
(2)
式(2)中, ;
;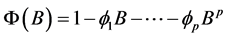 ,为平稳可逆
,为平稳可逆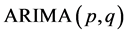 模型的自回归系数多项式;
模型的自回归系数多项式; ,为平稳可逆
,为平稳可逆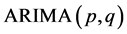 模型的移动平滑系数多项式。
模型的移动平滑系数多项式。
式(2)可以简记为:
 (3)
(3)
式(3)中, 为零均值白噪声序列。
为零均值白噪声序列。
由(3)式显而易见,ARIMA模型的实质就是差分运算与ARMA模型的组合。这说明任何非平稳序列只要通过适当阶数的差分实现差分后平稳,就可以对差分后序列进行ARMA模型拟合了。
2.2.2. ARIMA模型建立的基本步骤
1) 根据所收集的时间序列数据,利用SPSS或Eviews软件作出该时间序列的散点图;
2) 通过ADF单位根检验,判断该序列的平稳性;
3) 对非平稳序列进行平稳化处理,通常对其进行差分运算使其变为平稳序列;
4) 绘制差分序列的自相关和偏自相关图,并得到自相关系数(ACF)和偏自相关系数(PACF)表;
5) 确定 模型的阶数
模型的阶数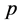 和
和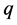 ,其中
,其中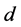 为差分的次数;
为差分的次数;
6) 估计模型的参数,并检验其是否具有统计意义;
7) 对残差序列进行白噪声检验;
8) 运用已通过检验的模型进行预测分析。
2.3. 混合时间序列模型
本文所谓的混合时间序列模型就是趋势外推法和ARIMA模型的结合,即先对时间序列配合趋势模型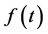 ,用来描述序列中的趋势分量,对于非趋势性分量,即趋势值与实际值的离差序列,再用ARIMA模型进行描述,最后把两个模型叠加起来进行预测研究[11] 。
,用来描述序列中的趋势分量,对于非趋势性分量,即趋势值与实际值的离差序列,再用ARIMA模型进行描述,最后把两个模型叠加起来进行预测研究[11] 。
混合时间序列模型可表示为:
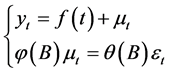 (4)
(4)
其中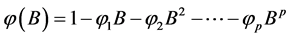 ,
,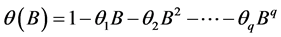 ,
,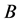 为滞后算子,
为滞后算子,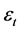 是服从正态分布的白噪声误差项。
是服从正态分布的白噪声误差项。
3. 实证分析
3.1. 数据来源及说明
根据《云南省统计年鉴–2011》和《云南省统计年鉴–2012》,本文收集了云南省1978到2011年的能源消费总量数据,将1978~2007年的数据[12] 作为训练集,建立预测模型,而2008~2011年的数据作为测试集,用于检验模型的预测效果,进而对云南省未来能源消费总量作出合理的预测。
将1978~2007年云南省能源消费总量记为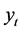 序列,其中
序列,其中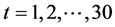 (1978年对应
(1978年对应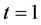 ),时间
),时间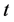 为自变量,
为自变量, 为因变量。
为因变量。
3.2. 云南省能源消费总量的预测模型建立
3.2.1. 建立趋势外推模型
1) 绘制时间序列趋势图
运用Eviews软件绘制1978~2007年云南省能源消费总量的散点图,见图1:
2) 模型选择及曲线估计
观察散点图,发现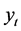 随时间的变化呈现逐渐上升的趋势,我们可尝试建立以时间
随时间的变化呈现逐渐上升的趋势,我们可尝试建立以时间 为自变量,
为自变量, 为因变量的二次曲线、三次曲线和指数曲线模型,曲线估计结果见表1。
为因变量的二次曲线、三次曲线和指数曲线模型,曲线估计结果见表1。