给定运动轨迹的凸轮–连杆组合机构的解析法设计

Analytical Design of the Line Cam-Linkage Combined Mechanism with the Given Movement

摘要: 根据输出轨迹点的运动与凸轮旋转同步的思路，给出并解决了按给定的轨迹曲线来设计凸轮–连杆组合机构的凸轮轮廓线的解析设计方法。通过实例对设计方法进行了验证。

Abstract: According to the idea of the output trace point movement synchronizing with cam rotation, an analytical design method about cam contour line of cam-linkage mechanism movement is intro-duced and resolved based on given track curve. An example is given to illustrate the design method.

1. 前言

凸轮连杆组合机构是由连杆机构和凸轮机构按一定的工作要求组合而成。它兼有凸轮和连杆机构的特性，控制准确有效，结构紧凑。能够输出任意复杂的运动轨迹或者实现特定的要求 [1] 。凸轮连杆组合机构是一种正在快速发展应用的组合机构，能够实现整周回转，具良好的动力性能和运动的可靠性 [2] 。因此，连杆凸轮机构在轻工机械、纺织食品，特别是精度要求较高的标准零件制造，仪器仪表行业得到越来越广泛的应用 [3] 。现有文献中，对于凸轮连杆组合机构的设计研究并不多，文献 [4] 是在作图法的基础上来反求凸轮廓线的设计方法，具有局限性。在本文中，根据实际给定的，较为一般性的轨迹曲线要求(某编织机输出机构的运动轨迹可近似为为半椭圆和半圆组成的封闭曲线)，运用文献 [5] 中对于组合机构的分析方法来进行设计，更具有实际意义和一般性。

2. 机构综合

2.1. 机构分析

如图1所示凸轮–连杆组合机构是以凸轮、构件BCM、构件DEF和连杆CD为基础的。利用滚子摆动从动件凸轮机构来控制输入和输出运动间的关系，从而使M点输出给定的运动轨迹。从设计角度来讲，因轨迹已知，且A点坐标、E点坐标、杆CD的长度L_CD，杆DE的长度L_DE，杆CM的长度L_CM，杆EF的长度L_EF，可根据机构的总体布置由设计者预先确定，因此杆MB和杆AB(B点是属于凸轮上的点)组成第一个RRRⅡ级杆组(ABM)，杆CD和杆DE组成第二个RRRⅡ级杆组(EDC)。

Figure 1. Starting position of cam-linkage mechanism movement

图1. 凸轮–连杆组合机构运动起始位置

2.2. 设计方法

2.2.1. 确定尺寸

建立固定坐标系。要根据设计的实际需要来选择，坐标系XAY如图1中所示。根据总体需求及机构动力学性能，适当选取定点E的坐标(X_E,Y_E)，杆CD的长度L_CD，杆DE的长度L_DE，杆CM的长度L_CM，杆EF的长度L_EF，杆BC的长度L_BC，杆DF的长度L_DF。

2.2.2. 建立已知轨迹的方程

固定坐标系XAY建立以后。此时M点在XAY中的轨迹就确定了。取合适起始点M₀，使M点按规定运动方式运动。将轨迹曲线任意分割成N个分点，每一分点对应一指针I，可得M点的轨迹坐标参数方程：

(1)

其中：。根据实际需要取定N，为了使设计更精确，N应足够大(可取凸轮廓线点数的10倍)。

在设计过程中，除了用到M点的轨迹坐标外，还用到M点的速度。对于所要设计的凸轮廓线，只要所实现M点的轨迹不变，其速度的大小和变化并不产生影响。为了简单起见，可令，得M点的速度为：

(2)

2.2.3. 确定杆AB、BM杆的长度L_AB、L_BM

在设计中，点A与点M的位置已知。让I = 1到N，步长为1进行循环，对于每一个I调用判断语句程序，可得到杆A点和M点间的最远距离(L_AM)_max和最近距离(L_AM)_min，以及相应的指针I_max和I_min。当L_AM分别处于(L_AM)_max和(L_AM)_min时，杆AB和BM分别为拉直共线和重迭共线位置。于是可得杆AB和杆BM的长度：

(3)

2.2.4. 求凸轮在与其固连的动坐标系中的轨迹坐标

让I = 1到N且步长为10 (步长为10的目的是使得I避开I_max和I_min，以避免出现杆AB和杆MB两杆共线，无法进行运动分析的位置)进行循环。将杆AB和杆MB看成一个RRR Ⅱ级杆组进行分析。因为AB相当于曲柄，在运动过程中，杆AB和杆MB所组成的RRR Ⅱ级杆组装配模式会发生改变(如图2所示，实线A、B、M三点逆时针和虚线A、B、M三点顺时针在求解时是不同的装配模式)，装配模式的改变发生在AB和MB共线的两位置，即I分别是I_min和I_max两处。装配模式不一样，则运动分析时调用杆组的方式也就不一样，因此要进行判断。具体方法如下：设凸轮逆时针转动，在AB、MB的初始位置，A、B、M三点为逆时针布置(如图2中实线所示)。如果，A、B、M三点逆时针排列，则调用RRR(ABM)；如果或，A、B、M三点顺时针排列，则调用RRR(MBA)。这样可求出AB、MB的位置及运动参数、和、。调用杆组子程序Link(MC)，求出C点在XAY坐标系中的坐标X_C、Y_C及运动参数V_XC、V_YC、A_CX、A_CY。调用RRR(EDC)，这样可求出ED、CD的位置及运动参数、和、。调用杆组子程序Link(CD)，Link(EF)，求出D点和F点在XAY

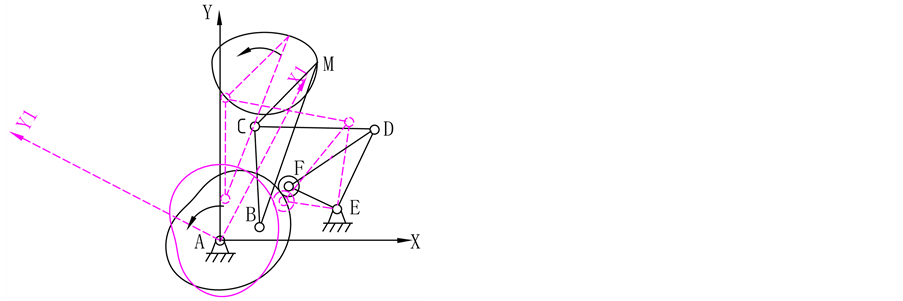
Figure 2. Cam-linkage mechanism (the dotted line represents the rotated figure)

图2. 凸轮–连杆组合机构(虚线是旋转后的图形)

坐标系中的坐标X_D、Y_D、X_F、Y_F及运动参数V_XD、V_YD、A_DX、A_DY、V_XF、V_YF、A_FX、A_FY。令 (其中为I = 0时杆AB的初始角度)。因动坐标系X₁AY₁与凸轮固连，则动坐标系X₁AY₁与定坐标系XAY之间的夹角为。由坐标变换可得F点在X₁AY₁动坐标系中的坐标(即凸轮的理论廓线在定坐标系XAY中的坐标)：

(4)

2.2.5. 求凸轮实际廓线的坐标X_T、Y_T

滚子摆动件盘形凸轮的实际廓线是以理论廓线上各点为圆心，以滚子半径R_r为半径的圆族的包络线。因此，凸轮实际廓线在X₁AY₁坐标系中的坐标方程为 [6] ：

(5)

若凸轮逆时针转动，则M = +1;否则M = −1。上面一组“−”、“+”号用于外包络线，下面一组“+”、“−”号用于内包络线。

式(5)中和的公式分别为：

(6)

3. 实例

某编织机输出机构的运动轨迹可近似为为半椭圆和半圆组成的封闭曲线，建立如图1所示的固定直角坐标系XAY，M点的轨迹为：以O (30,120)为中心，a = 35 mm，b = 20 mm的上半椭圆和r = 35 mm的下半圆组成的封闭轨迹。A点的坐标(0, 0)、E点的坐标(80, 20)、L_CM = 60、L_CD = 80、L_DE = 60、L_EF = 40滚子半径R₀ = 10 mm。根据公式(3)可求得L_AB = 27.9039 mm、L_MB = 139.331，由公式(4) (5) (6)求得凸轮的理论廓线和实际廓线在动坐标系X₁AY₁里的坐标参数，求得的凸轮廓线如图2所示。以上计算求解过程中，如果凸轮廓线出现尖点，则需要调整杆长尺寸及连杆间的夹角，来达到设计要求。

4. 结论

本文运用了杆组装配模式发生改变的情况下来设计凸轮廓线的方法。介绍了按给定的较为一般性的轨迹曲线来设计凸轮–连杆组合机构的凸轮廓线的解析设计方法。该方法具有精度高、简便等优点，是凸轮–连杆组合机构设计的好方法。输出点运动是实际给定的较为一般性的轨迹曲线要求(某编织机输出机构的运动轨迹可近似为为半椭圆和半圆组成的封闭曲线)，更具有实际意义和一般性。