1. 引言
多相同步发电机与三相同步发电机相比,不仅能在一定程度上减小气隙磁场的谐波分量,从而提高电机的性能;还能优化电能变换器的单元设置,进一步使电力系统的可靠性提高。多相同步发电机还具有效率高、转矩密度大以及容错能力强等优势,在高铁、动车、航海、军事以及工业领域等场合得到了高度应用,并且多相同步发电机的应用领域也在逐渐扩大,目前已经发展到风力发电系统、电动机车以及核电冷却系统等场合,可见多相同步发电机具有更广的发展空间 [1] [2] [3] [4] 。
励磁电流作为发电机的主要运行数据的一部分,设计同步发电机的励磁绕组就要先计算出励磁电流的大小。在传统的电机设计中,往往采取磁路的计算方法来计算空载电压为额定电压时的励磁电流,然后再经过制作的小样电机进行试验的验证,这样不单使电机的设计周期延长,还增加了电机设计的本钱。并且磁路计算的方法在磁路结构较为特殊时,会导致计算的结果产生较大的偏差。由于计算机有限元软件功能在逐步增强,使得其普遍的应用在电磁场计算中。有限元法是从电机原有的物理模型出发,可以考虑饱和效应,能够改善传统方法的不足,可以将结果计算的更为准确。
2. 有限元软件
用于电磁场的仿真软件,有ANASYS、ANSOFT、FLUX、MotorSolve以及JMAG等,在这些仿真软件中,ANASYS软件可以在电场、磁场和声场等多方面进行研究 [5] [6] [7] ,是一种功能强大的有限元仿真软件 [3] ,它能和很多CAD软件相关联,从而可以和CAD软件进行数据间的互换和共享。
3. 有限元法仿真流程
3.1. 假设条件
由于电机原有模型比较庞大,为了简化模型,并且能够满足结果的计算精度,对所建物理模型作以下假设:
1) 电机轴向默认无限长,在二维XY平面坐标系中进行有关问题的计算分析。
2) 在交变的磁场中忽略涡流反应这一因素,这样就可以把同步发电机的磁场当作非线性的稳态磁场来进行研究。
3) 忽略位移电流,只考虑绕组电流中的基波。
3.2. 建模
电机建模方案的主要数据见表1。所建电机的二维模型见图1 [8] 。

Table 1. The main parameters of the machine
表1. 电机的主要参数
3.3. 赋材料属性及模型剖分
电机模型建立完之后,将相应的材料属性赋加到电机模型的相应区域。本文中在定子、转子绕组,槽楔区域以及气隙部分的相对磁导率设为1,定子、转子铁芯材料均赋硅钢片D-50WW270。
网格的剖分就是把电机模型划分为许多个小单元,把这些小单元定义为有限元 [9] 。网格划分的越小,虽然会使计算的结果更为精确,但是同样会使计算量增大,所以要对两者进行综合分析,以便采用适当的网格划分精度。采纳PLANE53六节点三角形单元对网格进行划分。由于气隙长度很小,网格划分较为密集的区域主要分布在气隙区域及周围齿槽区域,而剩余区域的网格划分则相对较为疏松,划分网格见图2。
3.4. 边界条件的确定
在静止媒介中的二维静态电磁场,其矢量磁位的关系式满足如下方程:
 (1)
(1)
式中,μ:相对磁导率;
Az:矢量磁位;
Js:外加的源电流密度。
假设磁场只分布在电机的内部,对电机模型的最外边设定边界条件,即选定定子的外圆边界,将其Z方向上的矢量磁位设为0,即Az = 0。
3.5. 加载电流密度
由于本文是在空载时对电机进行仿真,所以只在转子的导电区域加载电流密度。加载的电流方向作如下规定:与正Z轴同向为正,反之为负。
转子导电区域加载的电流密度为:
 (2)
(2)
式中,N1:转子绕组每槽导体数;
If:励磁电流;
a1:转子绕组并联支路数;
S1:转子导体截面积。
3.6. 后处理
利用ANSYS软件计算电机的感应电势,就要先取出一个周期中的气隙磁通密度的数值,在气隙中点线上设置一条半圆形路径,见图3。该路径以逆时针为正方向,从A点出发,经半个周期后到达B点结束。虽然设置的路径是180˚的空间位置,但是要将路径延拓为一个周期,以此来获取一个周期中的数据。规定气隙磁通密度的正方向为:出转子进定子。
在后处理过程中可以获得基波气隙磁通密度的幅值Bδ,并可以计算出每极磁通的最大值Φm为:
 (3)
(3)
式中,Φm:每极磁通最大值;
Bδ:基波气隙磁密幅值;
Sτ:每极磁通面积。
求解每相感应电动势E0为:
 (4)
(4)
式中:E0:每相感应电动势;
f:频率;
W1:定子每相串联总匝数;
kdp1:定子线圈基波绕组因数。
在励磁绕组中加载电流密度,电流在流经励磁绕组时会产生一个永恒而稳定的磁场,从而可以得到一个磁力线闭合回路。首先,估算励磁电流If = 430.0 A,由式子(2)可计算出转子导电区域所加载的电流密度J1 = 1.310 A/mm2。
图4所示是空载时磁力线的分布图,从图中可以很清晰地看到绝大多数磁力线是沿着主磁通方向的。
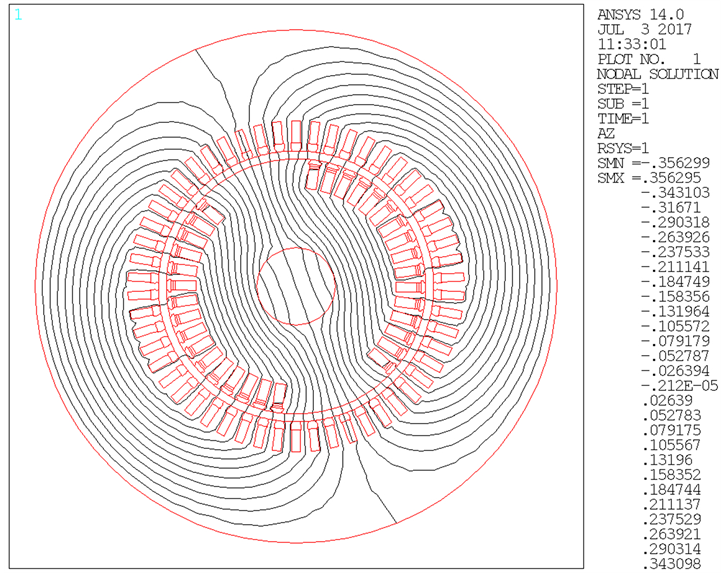
Figure 4. The distribution of magnetic field lines in no-load time
图4. 空载时磁力线分布图
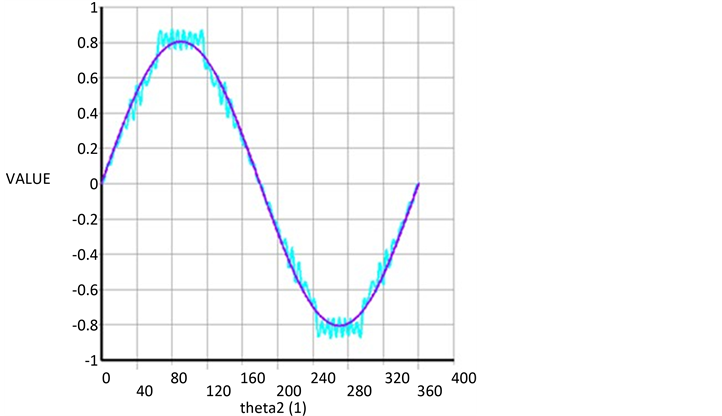
Figure 5. Air gap magnetically dense waveform in no-load time
图5. 空载时的气隙磁密波形
在规定了气隙磁通密度正方向的条件下,对气隙磁通密度采取傅里叶分解的方法,可以获得图5所示的气隙磁通密度波形图,其中,横坐标表示的是空间点角度,纵坐标表示的是气隙磁通密度的数值大小。
根据基波气隙磁密幅值Bδ,再由式(3)和(4)可分别求得每极磁通最大值Φm和每相空载感应电动势E0。在空载情况下E0和每相额定电压U1Φ应满足如下关系式:
 (5)
(5)
已知每相额定电压U1Ф = 1212 V,相对误差ε设为0.001。
若计算出的每相空载感应电势E0不符合式(5),则应该重新设置激磁电流If的大小,根据每相空载感应电动势E0与每相额定电压U1Φ的大小关系来对激磁电流If进行大小的设置,然后再对电磁场进行有限元法的求解运算,最终满足式(5)为止。
经迭代计算后可知,在If = 421.3 A的时候,气隙磁通密度的基波幅值Bδ = 0.8049 T,由公式(3)和(4)计算可得E0 = 1213 V,满足式(5),计算结束。
4. 结论
本文对有限元软件的仿真流程进行了较为详细的介绍,进而完成了对九相同步发电机的电机建模。在通用后处理阶段,由磁力线分布图可以得知绝大多数磁力线是走主磁通路线的,只存在极少数的漏磁通;由气隙磁通密度波形图中的基波幅值可计算得出每相的空载感应电势,再与每相额定电压进行比较,看是否满足所设定的条件,若不满足,则再次对激磁电流进行大小的设置,直到满足所设定的关系为止。
通过对电机二维仿真模型的建立以及对空载电压为额定电压时励磁电流的计算,为下一步研究稳态短路电流为额定电流时的励磁电流以及带额定负载时的励磁电流等不同工况下的励磁电流的大小打下了一定的基础。