1. 引言
随着信息技术的快速发展,社会经济活动和社会公共安全对于个人身份认证的要求越来越广泛。以人脸识别为代表的生物特征识别技术由于其便携性、唯一性和准确性以及不易遗忘等特点,成为身份认证发展的主流方向之一。以二维图像为代表的传统人脸识别方法容易受到光照、姿态、表情、年龄变化等因素的影响,在被识别对象非配合的情况下识别性能会有明显的下降 [1] 。近年来兴起的基于深度学习的二维人脸识别算法,虽然在大多数情况下已经取得了大量优异的成果,但是在识别目标具有大姿态变化和化妆、遮挡以及年龄变化等情况下,识别的精确性和稳定性依然存在较大问题。由于三维人脸能够提供更多的稳定鉴别信息,对姿态变化和年龄老化以及化妆、遮挡等情形具有更强的鲁棒性,因而利用三维人脸进行识别可以显著提高识别对象非配合情况下的识别性能。
2. 相关的工作
传统的三维人脸识别往往把人脸数据表示为深度图形式,深度图的表达形式以二维图像的方式内涵了三维的人脸结构数据。很多已有的二维人脸识别方法都可以直接应用到深度图上,如PCA、LDA、ICA和FisherFace等。但是这些方法对于姿态和表情等变化比较敏感,难以充分利用人脸的三维鉴别信息,识别的准确性和鲁棒性难以进一步提高。
由于人脸是非刚性的表明,姿态、表情等变化很容易造成人脸表象的较大变化。因此,克服姿态和表情等因素的变化带来的不利影响是三维人脸识别必须解决的关键问题。有些工作考虑提取如前额、鼻子、下巴等人脸的刚性区域 [2] ,用这些受表情变化较少的区域来进行分类识别。这些方法虽然提高了对表情变化的鲁棒性,然而却同时舍去了眼部、嘴巴等具有丰富鉴别信息的区域,造成信息的浪费,因而并没有在实质上解决表情变化带来的问题。还有一种解决姿态和表情变化的方法是基于三维形变模型的识别方法 [3] 。其思路是把人脸建模为一个三维的形变模型,通过模型参数的学习和调整来描述人脸表面的非刚性变化。这类方法需要足够多的训练数据,而对于如何保证形变模型的关键点的对齐质量仍是需深入研究。
一些研究者将三维的人脸数据映射到正视投影模型下来研究。Antonio Rama [4] 等提出了一种将多个视角下的人脸图像进行投影自动创建180˚人脸纹理图像的方法,进而根据关键点对纹理图像整体和人脸特征进行对准,最后使用对姿态变化较为鲁棒的P2CA方法进行分类,这种方法对于姿态变化具有较好的适应性,不过获取注册人脸数据时较为繁琐,装置较为复杂,而且需要注册人的主动配合。Liu [5] 等使用球面来建模人脸点云,把人脸深度数据投影为球面图像,对人脸的姿态变化影响具有很好的鲁棒性,不过他们仅仅利用了人脸的三维结构信息,没有利用人脸的纹理信息。
对于人脸识别来说,纹理信息与结构信息都是人脸的本征描述,具有一定的互补性 [6] 。近年来,也有研究人员也对结构和纹理多模态融合的人脸识别进行了研究。这些研究工作大多数是采用在决策层进行融合的方法,而在三维人脸识别中利用纹理信息的工作还比较少。如何充分利用三维人脸的结构和纹理信息进行充分融合而又不会带来计算和存储成本的大量增加,需要进一步深入的研究。
3. 三维人脸数据处理的问题
大多数的三维人脸数据表示形式是三维点云,这种表示形式占用了大量的存储空间,计算开销也非常大,在识别时不便于数据的处理和计算。如果能够把人脸三维点云用二维的形式表达,则可以大量节省空间存储和计算开销,对于特征表达和匹配也非常方便。本文提出一种三维人脸点云的二维表达形式,在不丢失信息的情况下,用更精简的表示形式来表达信息,使得海量的三维人脸存储和识别成为可能。
从方法上来说,已经有研究利用深度图像来表达三维人脸的数据。但这种方式只能存储人脸的空间结构信息,而对于同时包含丰富鉴别特征的人脸纹理信息则无法表达,从而导致识别的性能难以进一步提升。事实上,人脸的信息同时包含结构特征和纹理特征,结构和纹理信息都是对人脸生理特征的描述形式,综合利用两种特征可以更好的提取人脸的鉴别信息,改善识别系统的性能。从信息采集设备的角度来看,目前的三维人脸采集设备基本都可以在获取三维人脸结构信息的同时携带颜色纹理。因此,如果可以同时利用人脸三维结构信息和纹理信息这两种模态,就能够提取更为完整的人脸鉴别特征,通过多模态识别方法的融合来提高人脸识别系统的整体性能。
4. 三维人脸点云数据的对齐和映射
由于三维人脸的姿态各异,要进行统一的二维表示,首先需要对各姿态的三维人脸用一个统一的基准进行对齐。传统的对齐方法主要是通过三维人脸的关键点来进行。但是如果有些三维人脸数据是部分的,可能没有包含对齐所需的关键点,造成对齐的失败。考虑到人的三维头部数据基本上呈一个球体形状,如果以人脸数据进行球体拟合,则每个待识别的人脸三维数据都可以得到一个拟合的球心。进而,如果以球心和鼻线作为参考基点和基线进行对齐,就能够把各种姿态的三维人脸点云数据进行统一的对齐。因而,本文提出先对三维人脸点云数据进行球面拟合,再根据拟合球心和球面半径进行球面展开和映射的方式,把三维人脸展开为二维的球面图来表示。这种转换和展开方法不存在信息丢失,降低了存储成本,也有利于降低后续识别过程中的计算复杂度。
在三维人脸点云数据采集和处理时,原始采集数据是以采集设备为中心进行表达的。这种以不同采集设备为中心表达的数据具有不同的世界坐标系,要进行统一的处理,就需要进行数据的对齐,把不同设备采集的数据转换为同一个世界坐标系下的坐标。如果转换时把以采集设备为中心表达的笛卡尔坐标系转换为以采集对象为中心表达的坐标系统中,则有望降低采集目标姿态变化的影响,提高系统识别的鲁棒性。已有工作把三维人脸点云用圆柱面进行拟合,圆柱面拟合并展开的人脸图像具有较小的畸变,可以较好的保持人脸的外观特征。但是柱面映射需要先进行姿态矫正,而姿态估计较为繁琐,估计效果对最终的转换结果影响较大。由于球面映射对各种姿态都有统一的操作方式,可以消除平面内旋转引起的差异,为此本文采用球面变换的方法来进行转换。
为便于对原始的三维人脸点云进行坐标的球面变换,需要确定一个对于采集个体来说是相对稳定的球心位置。为此,本文提出使用原始的三维人脸点云进行球面拟合的方法来确定基准球面变换的球心。球面拟合是利用点云数据点的三维笛卡尔系坐标作为输入,求取特定的球面参数,使原始点云的集合距离拟合球面的距离在军方误差的意义下最小。利用高斯-牛顿法(Gauss-Newton)或莱文伯格-马奎尔特算法(Levenberg-Marquardt)可以求取拟合参数的近似解。但是高斯-牛顿法需要求解二阶海森矩阵,莱文伯格-马奎尔特需要经过多次迭代,在三维点云拟合时需要大量的计算时间。为了提高参数拟合时的求解速度,本文采用一种变量变换的方法,分两个阶段来求取拟合参数。在第一个阶段先把球面展开方程中的二次项设为中间变量,从而避免参数求解过程中的过多二次项计算。求得中间变量后再在第二个阶段通过简单计算求得拟合球面的球心坐标和拟合半径。这样就可以把带有二次项的非线性方程组的优化问题转变为线性方程组的求解问题,从而简化了计算。图1为三维人脸点云球面拟合的效果。
三维人脸点云数据球面拟合完成后,就可以利用拟合球心作为中心点,把各点的笛卡尔系下的三维坐标转换为球面坐标。球面坐标系下的人脸点云表示的是各点处距离球心的半径以及仰角和方位角的相互关系。从该方程中不难求得各点处半径与仰角和方位角的映射关系。为得到三维人脸点云的球面映射图,分别以仰角(范围为[0, π])和方位角(范围为[0, 2π])为横坐标轴和纵坐标轴的变量进行逐点立方插值,以插值点处的半径作为生成的球面展开图像的灰度值。所有插值都完成后,就可以得到以二维形式来表示的三维人脸点云的球面展开深度图像。同时,在插值时如果以颜色纹理作为插值对象,则可以同时生成球面展开的纹理图像。图2为生成的球面深度图像和球面纹理图像的效果。这种分别以深度形式和纹理形式表达的人脸信息在转换过程中没有信息丢失,可以逆向复原出原始的三维信息,同时减少了存储成本和计算开销,因而对于大数据量的三维人脸识别具有特别的实际价值。
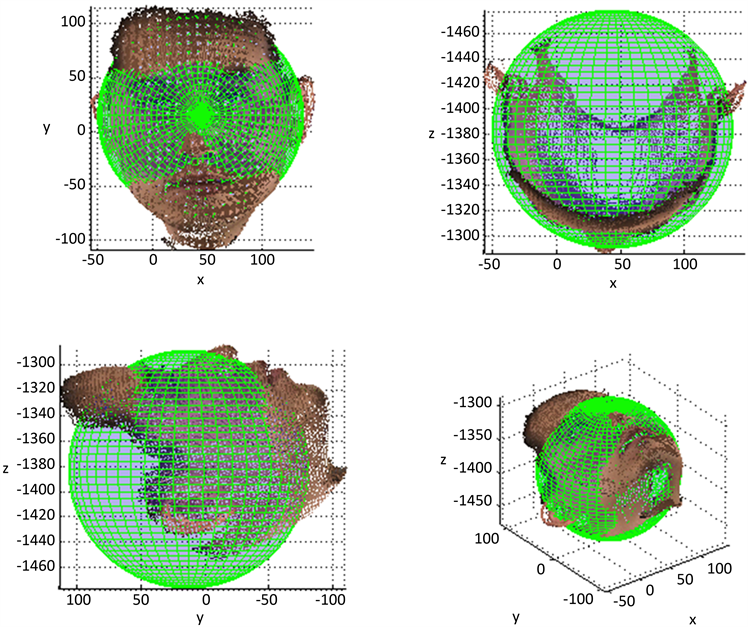
Figure 1. Spherical fitting effect of 3D human face point cloud
图1. 三维人脸点云的球面拟合效果

Figure 2. 2D representation of facial spherical depth map and texture map
图2. 二维形式表达的三维人脸球面深度图和纹理图
5. 结论
三维人脸识别中需要存储和处理大量的三维点云数据,存储和计算成本都很高。为便于实际应用中的存储和处理,本文提出了一种由二维球面展开图表示的人脸三维数据。对于待处理的三维人脸点云数据,可通过优化计算得到拟合的球心和半径等参数,利用该球心作为中心点就可以把原始点云数据变换到以拟合球心为原点的球面坐标系下。对原始三维人脸点云数据进行投影和插值就可得到映射到拟合球体表面的球面展开的深度图像。用同样的方法对原始点云的颜色信息进行插值就可以得到球面展开的纹理图像。这两种模态表示的球面展开图可以完整表达人脸三维表面特征而没有信息丢失,同时,对尺度、姿态和光照变化等因素的影响具有不变性。另外,不同姿态下获得的球面展开图消除了平面外旋转,对人脸识别应用中的存储和计算效率的提高都有实际意义。
基金项目
北京信息科技大学科研基金(1725013)。
NOTES
*通讯作者。