1. 引言
蓝光激光器是近年来激光研究的一个热点,它在高密度光存储、生物与医学检测、彩色显示、水下成像与通信以及先进制造业等领域有广泛应用 [1] [2] [3] 。非线性频率变换是获得蓝光激光的常用手段,一般利用二阶非线性效应获得蓝光激光,其非线性系数要比高阶的非线性系数大,这通常意味着更高的转换效率 [4] 。通过二阶非线性效应获得蓝光激光一般需要倍频(SHG)、和频(SFG)过程。对于400 nm~480 nm波段的蓝光,当基频光波长在800 nm~960 nm范围内时,可通过一次二阶非线性变换实现蓝光输出。例如Nd:YAG产生的946 nm光,可通过倍频方式实现473 nm蓝光 [5] ,Nd:GdVO4产生的880 nm激光,可通过倍频实现440 nm蓝光 [6] 。1319 nm、1342 nm光往往要先后经过倍频与和频来实现蓝光输出,即级联三倍频 [7] [8] 。要实现非线性频率变换,就要利用非线性晶体来产生非线性效应。对于三硼酸锂(LBO)、磷酸钛氧钾(KTP)、β-硼酸钡(BBO)等非线性晶体,需要通过角度相位匹配或温度相位匹配的方式满足相位匹配条件,实现非线性频率变换 [9] 。该方式必须按照特定方向切割晶体,维持在一个特定的工作温度,往往无法利用晶体的最大非线性系数,这限制了非线性转换效率的提高。对于角度相位匹配方式,两束偏振态不同的光在非线性晶体中传播时,会因双折射效应分离,产生走离效应,也会降低非线性转换效率。准相位匹配技术利用周期极化晶体实现非线性频率变换,理论上可以利用晶体的最大非线性系数,而且不会产生走离效应 [10] [11] [12] 。另外,LBO、KTP、BBO等晶体在实现级联三倍频过程中,倍频、和频的匹配角度或者匹配温度不一样,需要两块晶体分开实现倍频与和频过程,而且实现倍频、和频的两块晶体之间往往需要加入耦合系统,需要两个温控装置实现不同的温度控制。准相位匹配的方式,可通过单块周期极化晶体,不同极化周期实现倍频与和频,而且可以通过设计使其工作在同一温度。这种方式不再需要两块晶体之间的耦合,温度控制也更为简单。
2. 理论分析
通过准相位匹配方式实现非线性频率变换时,周期极化晶体中的耦合波方程如下:
(1)
dQ为周期极化晶体的有效非线性系数,表达式如下:
(2)
上式中,dH为周期极化晶体可利用的最大非线性系数;m为极化周期阶数,D为占空比,一般取D = 0.5,此时m应取奇数;Λ为极化周期。当极化周期阶数只取某一阶时,耦合波方程可化为:
(3)
极化周期应满足相位匹配条件:
(4)
根据公式(4),极化周期表达式为:
(5)
PPLN晶体色散方程中,晶体折射率是温度与波长的函数。晶体的Sellmeier方程如下 [13] :
(6)
方程中各参数如表1,表中参数引自参考文献13。
公式(6)中λ为波长,单位μm,T为温度,单位℃。
级联三倍频的倍频过程中
,和频过程中
,故某特定阶数的极化周期是温度与基频光波长的函数:
。以PPLN晶体实现1319 nm三倍频为例,倍频极化周期与和频极化周期与温度的关系如图1。

Table 1. Parameters of Sellmeier equation
表1. Sellmeier方程参数
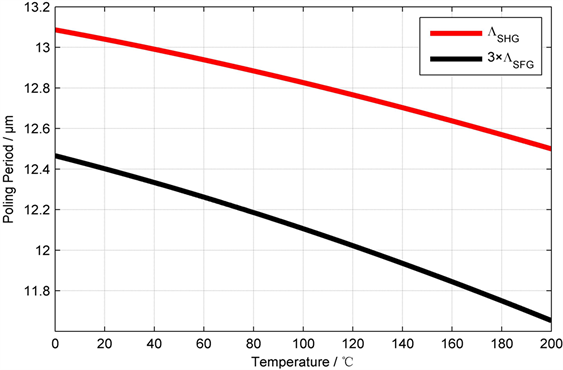
Figure 1. Relation of temperature and poling period
图1. 温度与极化周期的关系
确定工作温度后,倍频极化周期与和频极化周期即可确定。在理论工作温度30℃时,1319 nm倍频所需晶体极化周期为13.0 μm (m = 1),和频极化周期为12.4 μm (m = 3)。
3. 实验结果与分析
在确定极化周期后,利用5 mm倍频长度与35 mm和频长度,总长40 mm的PPLN晶体进行实验。实验装置简图如图2,采用声光调Q,偏振输出,45˚镜抑制1064 nm振荡,通过耦合透镜将基频光耦合进PPLN晶体,经过色散棱镜后,蓝光、红光、基频光分离。
基频光实验中,1319 nm光重频400 Hz,脉宽110 ns,光束质量
,
,光斑束腰
半径在经过耦合透镜后为0.406 mm (x)与0.4965 mm (y)。在基频光功率530 mW,工作温度55.5℃时,得到了最高2.4 mW的蓝光输出,此时红光功率为147 mW。实验测量了基频光入射耦合透镜前的功率以及
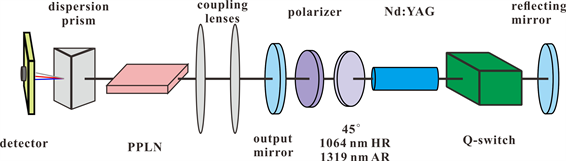
Figure 2. Experiment setup for third-harmonic generation
图2. 三倍频实验光路
经过色散棱镜后的出射光总功率,在基频光功率530 mW时,出射光总功率370 mW,约有30.2%的损耗。
实验测得的蓝光转换效率,在去掉损耗影响的情况下只有6‰。
实验测得基频光中心波长1318.8 nm,红光中心波长659.44 nm,蓝光中心波长为439.5 nm。
级联三倍频的设计方案中,经过倍频晶体部分后的倍频高斯光束与基频高斯光束之间的光斑面积比为1:2,参与和频过程的基频光占倍频后剩余基频光功率的63%,而理想的和频过程的倍频光与基频光光子数比为1:1,故要求倍频效率为55.75%,三倍频理想转换效率最高只有83.6%,无法达到100%。在实验中,红光功率147 mW,转换效率39.7%,需要提高光功率密度或者增加晶体长度提高转换效率。另外,实验发现PPLN晶体的理论工作温度与最高蓝光转换效率时的工作温度差距比较大,这主要由晶体的极化周期误差导致。
晶体的极化周期误差除引起工作温度的变化外,也会导致转换效率的下降。单一周期的周期极化晶体,极化周期误差可通过温度调节,补偿因此产生的相位失配。即:
(7)
对于有两个极化周期的晶体来说,倍频极化周期误差与和频极化周期误差并不相同,达到补偿条件的温度也各不相同,
,
。倍频与和频过程的理想工作温度为T0,相位匹配时的工作温度为
,
。级联三倍频需要先进行倍频过程,以倍频过程的工作温度TSHG为实际工作温度时,该温度下和频过程的相位失配量为
。
越大,和频过程的相位失配也就越大。相位失配所导致的和频效率下降,可用下面的公式表示:
(8)
其中,A为高斯光束级联三倍频时的最高转换效率,由上文分析可知,约为83.6%。公式右边第二项表示晶体长度一定,因极化周期误差导致相位匹配工作温度不同,引起相位失配时,对转换效率的影响。示意图如图3。
图中T表示倍频相位匹配时的工作温度而横坐标表示和频相位匹配时的工作温度,因极化周期误差,两者相位匹配时的工作温度并不相同,∆T即表示因此引起的倍频与和频的匹配温度差值。当两者相位匹配工作温度相同时,转换效率最高,为83.6%。两者相位匹配工作温度不同,当以倍频相位匹配温度为实际工作温度时,和频转换效率会下降。其中,T的值与∆T的值取决于晶体极化周期及其误差,晶体极化周期误差越大,转换效率下降越明显。另外,由公式(8)可知,当极化周期误差导致的相位失配量为定值时,晶体长度越长,转换效率下降越明显。

Figure 3. Diagram of relation between match-temperature for SFG and conversion efficiency
图3. 和频匹配温度与转换效率之间关系的示意图
通过以上分析,为提高转换效率需提高极化周期精度,减小误差,并合理设计晶体倍频与和频部分的长度。
4. 结论
实验证明,通过一块晶体,在同一温度下实现级联三倍频蓝光输出的方法是可行的。该方法与两块晶体分开实现倍频与和频的方式相比,温控以及整体结构更加简单;而且该方法不仅适用于1319 nm波长的级联三倍蓝光输出,在周期极化晶体透光波段范围内的其他波长也同样适用。通过进一步分析发现,提高晶体的极化周期精度,合理设计晶体的倍频与和频长度,实现高转换效率的三倍频输出是可能的。论文中的分析可为相关的级联三倍频设计提供参考。
基金项目
国家自然科学基金项目(61575099);中国工程物理研究院院长基金(201501023)。
[1] Sakuma, J., Asakawa, Y. and Obara, M. (2004) Generation of 5-W Deep-UV Continuous-Wave Radiation at 266 nm by an External Cavity with a CsLiB6O10 Crystal. Optics Letters, 29, 92. https://doi.org/10.1364/OL.29.000092
[2] Seyed, Ebrahim, Pourmand, et al. (2015) Effects of 946-nm Thermal Shift and Broadening on Nd^3+:YAG Laser Performance. Chinese Physics B, 24, 342-345.
[3] Wang, G., Geng, A., Bo, Y., et al. (2006) 28.4 W 266 nm Ultraviolet-Beam Generation by Fourth-Harmonic Generation of an All-Solid-State Laser. Optics Communications, 259, 820-822. https://doi.org/10.1016/j.optcom.2005.09.061
[4] Shen, Y.R. (1984) Principles of Nonlinear Optics. John Wiley, 261.
[5] Czeranowsky, C., Heumann, E. and Huber, G. (2003) All-Solid-State Continuous-Wave Frequency-Doubled Nd:YAG- BiBO Laser with 2.8-W Output Power at 473 nm. Optics Letters, 28, 432. https://doi.org/10.1364/OL.28.000432
[6] Castaing, M., Balembois, F. and Georges, P. (2008) Continuous-Wave Laser at 440 nm Based on Frequency-Doubled Diode-Pumped Nd:GdVO(4) Crystal. Optics Letters, 33, 1957-1959. https://doi.org/10.1364/OL.33.001957
[7] Mu, X., Ding, Y.J. and Zotova, T.B. (2005) All-Solid-State, Compact, and Coherent Blue Source Producing 118 mW at 440 nm by Intracavity-Frequency-Tripling Nd:YAG Laser Beam. IEEE (CLEO) Conference on Lasers and Electro-Optics, 473-475. https://doi.org/10.1109/CLEO.2005.201817
[8] Ogilvy, H., Piper, J.A. and Withford, M.J. (2005) Intracavity Second and Third Harmonic Generation at 671 and 447 nm from a Q-Switched Nd:GVO4 Laser. Advanced Solid.
[9] Koechner, W. (2005) Solid-State Laser Engineering/-5th Rev. and Updated ed. World Book Inc.
[10] Chen, Q. and Risk, W.P. (1994) Periodic Poling of KTiOPO4 Using an Applied Electric Field. 30, 1516-1517.
[11] Burns, W.K., Mcelhanon, W. and Goldberg, L. (1994) Second Harmonic Generation in Field Poled, Quasi-Phase- Matched, Bulk LiNbO3. IEEE Photonics Technology Letters, 6, 252-254. https://doi.org/10.1109/68.275441
[12] Zhai, K., Zhang, S., Ma, X., et al. (2016) Temperature Dependence of Fiber-Format Multiwavelength Generation Process in Bulk MgO-PPLN Crystal Via High-Power Photonic Crystal Fiber Laser. IEEE Photonics Journal, 8, 1-7. https://doi.org/10.1109/JPHOT.2016.2600373
[13] Gayer, O., Sacks, Z., Galun, E., et al. (2008) Temperature and Wavelength Dependent Refractive Index Equations for MgO-Doped Congruent and Stoichiometric LiNbO3. Applied Physics B, 91, 343-348. https://doi.org/10.1007/s00340-008-2998-2