基于改进UKF算法的动力电池SOC在线估计

Online Estimation of SOC in Power Cell Based on Improved UKF Algorithm

摘要: 为了更准确的估计电池荷电状态(SOC)，我们考虑了影响SOC估计精度的主要因素和传统SOC估计方法的缺点，运用递推最小二乘法进行电池模型参数辨识，实现了模型参数的实时修正，提高了模型精度。我们采用次优无偏MAP时变估计器对噪声协方差矩阵进行实时更新，结合无迹卡尔曼滤波算法进行SOC在线估计，改进了传统UKF算法，降低了噪声对SOC估算的影响。试验和仿真结果表明，改进后的UKF算法相比传统UKF算法具有更高的估算精度。

Abstract: In order to estimate the state of charge of the battery, the main factors affecting the accuracy of SOC estimation and the shortcomings of the traditional SOC estimation method are considered. Recursive least square (RLS) method is used to do the online identification of the parameter of the battery model, which can realize the real time correction of model parameters and improve the accuracy of the model. The suboptimal unbiased MAP time-varying estimator is adopted in this paper to real time update the noise covariance matrix. And it’s combined with the Unscented Kalman filter (UKF) for SOC online estimation, which improved traditional UKF algorithm and reduced the impact of noise on SOC estimation. Finally, the experiment and simulation show that the improved UKF has better accuracy in SOC estimation than the traditional UKF estimation.

1. 引言

电池管理系统(BMS)是电动汽车的重要组成部分之一，它的作用主要是监测动力电池组状态，保证其工作在合理的参数范围内。电池管理系统的关键技术包括热均衡技术、荷电状态(SOC)计算、健康状态(SOH)计算和安全快充技术等等。其中SOC能够反映动力电池组的剩余容量，从而得知电动汽车的续航里程，无疑是电池管理系统中最重要的参数之一。但由于SOC的不可直接测量性和锂电池系统的非线性，要实现对SOC高精度估算的难度很大 [1] 。

目前，国内外关于SOC计算的方法有很多，总结出来主要有以下几种：安时积分法、开路电压法、神经网络法和卡尔曼滤波法等 [2] 。其中，神经网络法由于模型复杂且模型精度依赖于训练数据集的完备性，因此还未在电动汽车上普及使用。而当前主要使用的开路电压法辅助安时积分法积分进行SOC估算，也有着不具备自我修正的能力和太过依赖传感器精度与SOC初值准确度的缺陷。卡尔曼滤波算法主要针对的是线性系统，而电池是一个强非线性系统，所以出现了改进的扩展卡尔曼滤波(EKF)算法，用泰勒展开的方法将非线性的状态方程线性化，但是这种线性化的方法由于忽略了泰勒展开的高阶项引入了较大的误差，且需要计算雅克比矩阵，计算量较大，对于在线估计存在一定的困难 [3] [4] [5] [6] 。针对EKF存在的缺陷，Julier等人提出了无迹卡尔曼滤波算法(UKF)，通过设计少量Sigma点，用Sigma点的分布逼近系统的状态分布，然后计算这些Sigma点经过状态方程的计算后，对其均值和方差的估算值采用UT变换，最后获得滤波值基于状态方程的更新 [7] [8] [9] [10] 。该方法省去了EKF的线性化步骤，减少了估算误差。但是电池模型在SOC估计上适应性差，并且模型的参数极易受外部因素影响 [11] 。采用离线辨识获取模型参数的方式不具备实时性，会影响到UKF的估算结果。而在线辨识能在电池工作过程中对模型参数进行实时更新修正，更有利于SOC的估算。由于电池在实际使用中，存在的系统噪声会随着实际工况而产生变化，具备很强的随机性 [12] ，若是将有色噪声单纯简化为白噪声，无疑会影响SOC估算的精度。

本文运用递推最小二乘法对模型参数进行在线辨识，采用次优无偏MAP时变估计器对噪声协方差矩阵进行在线更新，并结合无迹卡尔曼滤波算法进行SOC在线估计，改进了传统UKF算法，降低了模型和噪声对于SOC估算的影响。

2.电池模型及其参数辨识

2.1. 电池模型的建立

本文选取Thevenin等效电路模型来模拟电池实际工作时的内部变化特性，如图1所示。

该等效电路是由电池电动势、一个纯电阻和一个电容电阻并联回路串联组成，其系统离散化状态空间方程为：

$\left[\begin{array}{c}{U}_{p,k}\\ SO{C}_k\end{array}\right]=\left[\begin{array}{cc}1-\frac{\Delta t}{C_p{R}_p}& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}{U}_{p,k-1}\\ SO{C}_{k-1}\end{array}\right]+\left[\begin{array}{c}\frac{\Delta t}{C_p}\\ \frac{\eta \Delta t}{C_0}\end{array}\right]\left[I_{k-1}\right]+{\omega }_k$ (1)

$U_{t,k}=\left[\begin{array}{cc}1& 0\end{array}\right]\left[\begin{array}{c}{U}_{p,k}\\ SO{C}_k\end{array}\right]+\left[R_e\right]\left[I_k\right]+OCV+{\nu }_k$ (2)

OCV为电池开路电压，U_t为电池输出端电压，R_e为电池的欧姆电阻，用来模拟电流突变时的电阻特性，R_p和C_p分别为电池的极化内阻和极化电容，它们并联构成容阻回路，用来模拟电池在极化效应表现出的端电压渐变的特性。 $\Delta t$ 为采样间隔， ${\omega }_k$ 、 ${\nu }_k$ 为随机干扰，通常当作高斯白噪声处理。

2.2. 电池模型参数在线辨识

电池模型参数辨识方法分为离线辨识和在线辨识两种。针对实际工作时，电池模型参数会随着温度、SOH等各种因素而发生变化，本文采用递推最小二乘法对参数R_e、R_p、C_p进行在线辨识，其优点是能够进行实时修正，保证模型的精度，满足SOC估算的需求。

构造观测向量 ${\phi }_k=\left[y_{k-1},I_k,I_{k-1}\right]$ ，参数向量 ${\theta }_k={\left[\alpha ,\beta ,\gamma \right]}^{\text{T}}$ ，其中

$y_k=U_{t,k}-OCV=U_{p,k}+I_k{R}_{e,k}=\left(1-\frac{\Delta t}{C_{p,k-1}{R}_{p,k-1}}\right)U_{p,k-1}+\frac{\Delta t}{C_{p,k-1}}{I}_{k-1}+R_{e,k}{I}_k$ (3)

基本观测模型为：

$y_k={\phi }_k{\theta }_k$ (4)

Figure 1. Thevenin equivalent circuit model

图1. Thevenin等效电路模型

对观测方程进行差分处理可得差分方程：

$y_k=\alpha y_{k-1}+\beta I_k+\gamma I_{k-1}$ (5)

其中 $\alpha ,\beta ,\gamma$ 是观测向量的参数。

联立(3)、(5)可得：

$\{\begin{array}{l}\alpha =1-\frac{\Delta t}{C_{p,k-1}{R}_{p,k-1}}\\ \beta =R_{e,k}\\ \gamma =\frac{R_{p,k-1}\Delta t+R_{e,k-1}\Delta t-C_{p,k-1}{R}_{p,k-1}{R}_{e,k-1}}{C_{p,k-1}{R}_{p,k-1}}\end{array}$ (6)

然后开始递推最小二乘法的循环计算：

1) 对初始时刻的各参数进行初始化，并设定初始时刻为k − 1时刻，初始化对象包括观测变量的协方差矩阵 $P_0$ ，参数向量 ${\theta }_0$ 和遗忘因子 $\lambda$ 。

2) 通过初始时刻端电压和开路电压，根据公式(5)，计算k时刻的 ${\phi }_k$ 。

3) 计算k时刻的增益矩阵 $L_k$ ：

$L_k=\frac{P_{k-1}{\phi }_k}{\lambda +{\phi }_k^T{P}_{k-1}{\phi }_k}$ (7)

4) 计算k时刻的观测向量协方差矩阵 $P_k$ ：

$P_k=\frac{P_{k-1}-L_k{\phi }_k^{\text{T}}{P}_k}{\lambda }$ (8)

5) 计算k时刻的观测模型参数向量 ${\theta }_k$ ：

${\theta }_k={\theta }_{k-1}+L_k{e}_k$ (9)

其中 $e_k$ 是观测量的估计误差：

$e_k=y_k-{\phi }_k^{\text{T}}{\theta }_k$

6) 得到 ${\theta }_k$ 后，就可以得到 $\alpha ,\beta ,\gamma$ ，然后通过公式(6)反推可得更新后的 $C_p,R_p,R_e$ ，从而根据上一个时刻的电池状态，完成了模型参数的实时更新。

3. 基于改进的UKF滤波算法的SOC在线估计

3.1. UKF算法理论

无迹卡尔曼滤波算法是基于无迹变换的一种算法，其基本原理是利用采样点(也称为sigma点)的分布来近似非线性目标函数的概率分布。

目前sigma点的采样策略有很多，例如单形采样、对称采样等等。取sigma点方式也有两种：取一次sigma点或者取两次sigma点来代替非线性函数。

本文选择使用对称采样策略和一次取sigma点来代替非线性函数，Sigma点个数为3。n为非线性系统中状态变量的维数，这里取1。

UKF具体算法过程如下：

1) 计算权重：

$\lambda ={\alpha }^2\left(n+\kappa \right)-n=2$ (11)

$W_0^m=\frac{\lambda }{n+\lambda }=\frac{2}{3}$ (12)

$W_0^c=\frac{\lambda }{n+\lambda }+\left(1-{\alpha }^2+\beta \right)=\frac{8}{3}$ (13)

$W_i^m=W_i^c=\frac{1}{2\left(n+\lambda \right)}=\frac{1}{6},i=1,2,\cdots ,2n$ (14)

2) 初始化：

$\overline{x_0}=E\left(x_0\right),P_0=E\left(x_0-\bar{x}\right){\left(x_0-\bar{x}\right)}^{\text{T}}$ (15)

3) sigma点采样：

采取对称采样的取点策略：

$x_{k-1,0}=x_{k-1}$

$x_{k-1,i}=x_{k-1}+\sqrt{\left(n+\lambda \right)P_{k-1}},i=1,2,\cdots ,n$ (16)

$x_{k-1,i}=x_{k-1}-\sqrt{\left(n+\lambda \right)P_{k-1}},i=n+1,n+2,\cdots ,2n$

4) 预测更新：

$x_{k,i}=f\left(x_{k-1,i}\right),\overline{x_k}={\displaystyle \underset{i=0}{\overset{i=2n}{\sum }}{W}_i^m}{x}_{k,i}$ (17)

$\widehat{P_k}={\displaystyle \underset{i=0}{\overset{i=2n}{\sum }}{W}_i^c\left(x_{k,i}-\overline{x_k}\right){\left(x_{k,i}-\overline{x_k}\right)}^{\text{T}}}+Q_k$ (18)

$Q_k$ 为过程噪声，在传统的UKF估计算法中通常简化为高斯白噪声。

5) 测量更新：

$Y_{k,i}=g\left(x_{k,i}\right)$ (19)

$\overline{Y_k}={\displaystyle \underset{i=0}{\overset{2n}{\sum }}{W}_i^m{Y}_{k,i}}$ (20)

$P_{Y_k,Y_k}={\displaystyle \underset{i=0}{\overset{i=2n}{\sum }}{W}_i^c\left(Y_{k,i}-\overline{Y_k}\right){\left(Y_{k,i}-\overline{Y_k}\right)}^{\text{T}}}+R_k$ (21)

$P_{x_k,Y_k}={\displaystyle \underset{i=0}{\overset{i=2n}{\sum }}{W}_i^c\left(x_{k,i}-\overline{Y_k}\right){\left(Y_{k,i}-\overline{Y_k}\right)}^{\text{T}}}$ (22)

$R_k$ 为测量噪声，在传统的UKF估计算法中通常简化为高斯白噪声。

6) 最优估计：

$K=P_{x_k,Y_k}/P_{Y_k,Y_k}$ (23)

$e_k=Y_k-\overline{Y_k}$ (24)

$x_k=\overline{x_k}+e_{k}G$ (25)

$P_k=\widehat{P_k}-K{P}_{Y_k,Y_k}{K}^{\text{T}}$ (26)

3.2. 噪声更新

电池在实际使用过程中，过程噪声和测量噪声的统计特性会随着实际工况的变化而变化，具有很强的随机性。而在传统UKF算法中，通常将噪声简化为高斯白噪声处理，这会影响到SOC估算的精度。本文采用次优无偏MAP时变估计器对噪声协方差矩阵进行实时更新，数据加权策略为渐消记忆指数加权法，降低了噪声对SOC估算的影响，改进了传统的UKF估计算法。

基于次优无偏MAP时变估计器的噪声更新公式如下：

${\omega }_k=\left(1-d_k\right){\omega }_{k-1}+d_k\left(x_{k-1}-A_{k-1}{x}_{k-1}\right)$ (27)

${\nu }_k=\left(1-d_k\right){\nu }_{k-1}+d_k\left(x_{k-1}-A_{k-1}{x}_{k-1}\right)$ (28)

$Q_k=\left(1-d_k\right)Q_{k-1}+d_k\left(K{e}_k{e}_k^{\text{T}}{K}^{\text{T}}\text{+}{P}_k+\widehat{P_k}\right)$ (29)

$R_k=\left(1-d_k\right)R_{k-1}+d_k\left(e_k{e}_k^{\text{T}}-P_{Y_k,Y_k}\right)$ (30)

式中b为遗忘因子，一般取0.95， $x_k=\left[\begin{array}{c}{U}_{p,k}\\ SO{C}_k\end{array}\right]$ ， $A_{k-1}=\left[\begin{array}{cc}1-\frac{1}{C_p{R}_p}& 0\\ 0& 1\end{array}\right]$ ， $K$ 为UKF中的卡尔曼增益， $$ 为加权系数， $d_k=\frac{1-b}{1-b^k}$ 。

将计算所得的 ${\omega }_k$ 、 ${\nu }_k$ 、 $Q_k$ 、 $R_k$ 代入公式(1)、(2)、(18)、(21)中，即可完成SOC在线估计过程中噪声协方差的实时更新，替代了传统UKF算法中用高斯白噪声来代替系统噪声的方法，从而解决了噪声带来了误差问题。

4. 试验验证

本试验主要用于验证基于递推最小二乘法的电池模型参数在线辨识和基于改进的UKF算法的SOC估算的准确性。通过电池测试设备对一节容量为35 Ah的三元材料锂电池分别进行HPPC试验和DST动态工况试验，使用设备监测的SOC作为SOC真值，使用设备传感器测量的端电压作为真实端电压，与在线辨识结果和基于改进UKF的SOC估算值作对比。

首先验证基于递推最小二乘法的模型参数在线辨识的准确性。图2为HPPC试验过程中在线辨识实

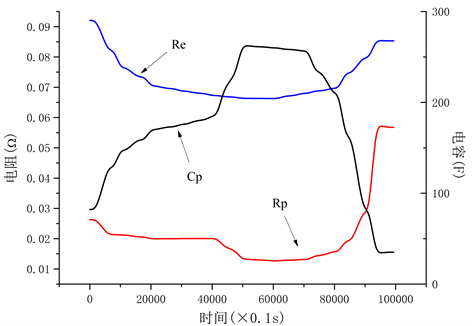
Figure 2. Curve: The change of battery model parameters with time

图2. 电池模型参数随时间的变化图

时获得的电池模型各参数随时间变化的曲线。由于模型中各参数难以直接测量，无法验证辨识结果的准确性，故根据实时获得的模型参数计算得到端电压并与真实端电压进行比较，图3为真实端电压与在线辨识和离线辨识两种方法获取的估算端电压的对比。结果可以看出，在线辨识获取的模型参数计算所得的估算端电压与真实端电压更加吻合，误差更小。可以表明在线辨识得到的模型参数更为准确，模型精度更高。

图4为DST动态工况下改进UKF算法与传统UKF算法的SOC估算效果对比，可以看出改进后的UKF和传统UKF的估算曲线与SOC真值曲线都能较好的吻合。为了更好的进行估算结果比较，图5给

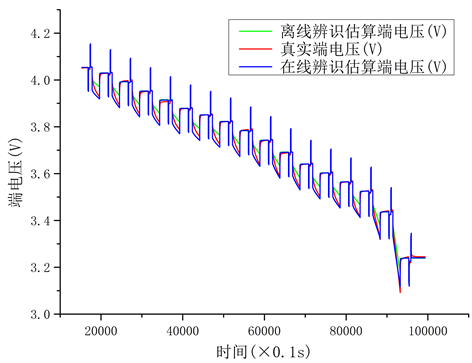
Figure 3. Curve: Comparison between off-line identification and on-line identification of voltage

图3. 离线辨识和在线辨识估算端电压与真实端电压对比

Figure 4. Curve: Comparison of SOC estimation between the two methods and the true value

图4. 两种方法的SOC估算值和真值对比

Figure 5. Curve: SOC estimation error of two methods

图5. 两种方法的SOC估算误差

出了两种方法估算结果对比真值的误差曲线。由图5可以看出，在工况前6000秒，传统UKF和改进后的UKF估算误差都低于3%，但是在600秒以后，传统UKF的估计误差迅速增大，而改进的UKF估算误差则基本保持不变。虽然在7000秒后，改进的UKF算法估算误差也有增加，但最高也未超过2.5%。从整个工况来看，传统UKF算法的抑制误差能力不如改进的UKF算法。由此可见，相比于传统UKF中将噪声简化为高斯白噪声，使用次优无偏MAP时变估计器对噪声协方差矩阵进行实时更新后，确实减小了算法中出现的误差，提升了SOC估算的精度。

5. 结论

1) 基于递推最小二乘法的电池模型参数在线辨识具有更好的实时性和可靠性，能够在电池工作状态下实时获得模型参数，提高模型精度，相比于离线辨识具有更好的实用性。并且从试验和仿真结果来看，在线辨识的估算结果相比离线辨识更为准确。

2) 基于改进的UKF算法的SOC在线估计通过次优无偏MAP时变估计器对噪声协方差矩阵进行实时更新，降低了噪声对于SOC估算的影响，在锂电池动态工况下的估算效果优于传统的UKF算法。从试验和仿真结果来看，改进的UKF算法在抑制误差方面明显优于传统UKF算法，并且能将误差始终维持在2.5%以下。

参考文献

[1] 胡志坤, 刘斌, 林勇, 等. 电池SOC的自适应平方根无迹卡尔曼滤波估计算法[J]. 电机与控制学报, 2014, 18(4): 111-116.

[2] 李洪宇, 张晓强, 张卫平. 大容量锂离子电池SOC估算原理及应用[J]. 电源技术, 2015, 39(5): 1100-1102.

[3] 董超, 尚鸿, 杜明星. 基于扩展卡尔曼滤波法的锂离子电池SOC估算[J]. 制造业自动化, 2014(11): 21-23.

[4] 徐颖, 沈英. 基于改进卡尔曼滤波的电池SOC估算[J]. 北京航空航天大学学报, 2014, 40(6): 855-860.

[5] 赵又群, 周晓凤, 刘英杰. 基于扩展卡尔曼粒子滤波算法的锂电池SOC估计[J]. 中国机械工程, 2015, 26(3): 394-397.

[6] 刘艳莉, 戴胜, 程泽, 等. 基于有限差分扩展卡尔曼滤波的锂离子电池SOC估计[J]. 电工技术学报, 2014, 29(1): 221-228.

[7] Julier, S., Uhlmann, J. and Durrant-Whyte, H.F. (2000) A New Method for the Nonlinear Transformation of Means and Covariances in Filters and Estimators. IEEE Transactions on Automatic Control, 45, 477-482. https://doi.org/10.1109/9.847726

[8] Aung, H., Low, K.S. and Shu, T.G. (2015) State-of-Charge Estimation of Lithium-Ion Battery Using Square Root Spherical Unscented Kalman Filter (Sqrt-UKFST) in Nanosatellite. IEEE Transactions on Power Electronics, 30, 4774-4783. https://doi.org/10.1109/TPEL.2014.2361755

[9] Zhang, J. and Xia, C. (2011) State-of-Charge Estimation of Valve Regulated Lead Acid Battery Based on Multi-State Unscented Kalman Filter. International Journal of Electrical Power & Energy Systems, 33, 472-476. https://doi.org/10.1016/j.ijepes.2010.10.010

[10] Partovibakhsh, M. and Liu, G. (2015) An Adaptive Unscented Kalman Filtering Approach for Online Estimation of Model Parameters and State-of-Charge of Lithium-Ion Batteries for Autonomous Mobile Robots. IEEE Transactions on Control Systems Technology, 23, 357-363. https://doi.org/10.1109/TCST.2014.2317781

[11] 孙豪豪, 潘庭龙, 吴定会. 基于自适应电池模型的SOC加权在线估计[J]. 系统仿真学报, 2017, 29(8): 1677-1684.

[12] 邹峰, 陈则王. 基于改进扩展卡尔曼滤波算法的锂离子电池荷电状态估计[J]. 机械制造与自动化, 2017(5): 130-133.

知网检索的两种方式：

1. 打开知网页面http://kns.cnki.net/kns/brief/result.aspx?dbPrefix=WWJD

下拉列表框选择：[ISSN]，输入期刊ISSN：2164-540X，即可查询

2. 打开知网首页http://cnki.net/

左侧“国际文献总库”进入，输入文章标题，即可查询

投稿请点击：http://www.hanspub.org/Submission.aspx

期刊邮箱：[e-mail]