孪晶界和温度对纳米多晶铁变形机制影响的模拟研究

Effect of Twin Boundary and Temperature on Deformation Mechanism of Nano-Polycrystal Iron by Molecular Dynamics

摘要: 本文采用分子动力学模拟方法研究了在拉伸载荷下，孪晶界和温度对纳米多晶铁力学性能的影响。研究结果表明：杨氏模量随着孪晶厚度的增大而增大；在温度为10 K或300 K下，当孪晶厚度小于临界尺寸时，峰值应力都随着孪晶厚度的增大而增大，表现出反常的Hall-Petch的现象，当孪晶厚度大于临界尺寸时，峰值应力随着孪晶厚度的增大而减小，表现出Hall-Petch的现象；温度为10 K时的临界值明显低于温度为300 K的临界值，这说明温度的变化影响着临界值；模型中的孪晶界上由于应力的集中，使得孪晶界成为萌生变形孪晶的源，促进了塑性变形，这是孪晶界对于纳米多晶铁弱化的主要原因。此外，也观察到裂纹的成核、孪晶界迁移和退孪晶的现象。

Abstract: The effects of twin boundary and temperature on the mechanical properties of nano-polycrystal iron under tensile loading were studied by molecular dynamics simulation. The results show that the Young’s modulus increases with the increase of twin thickness. At temperatures of 10 K and 300 K, when the twin thickness is smaller than the critical size, the peak stress increases with the in-crease of the twin thickness, showing abnormal Hall-Petch phenomenon. However, when the twin thickness is larger than the critical size, the peak stress decreases with the increase of twin thickness, indicating the Hall-Petch relationship. When the temperature is 10 K, the critical size is obviously lower than the critical size of 300 K, which indicates that the temperature affects the critical size. The twin boundary in the model becomes the initiation source of the deformation twin due to the stress concentration, promoting the plastic deformation, which is the main reason for the weakening of nano-polycrystal iron. In addition, the phenomena of crack nucleation, twin boundary migration and twin retreat are also observed.

1. 引言

纳米金属由于其独特的机械性能而被广泛研究，大量的实验和分子动力学(MD)模拟研究表明纳米金属材料是一种具有高强度和高延展性的超塑性材料 [1] [2] [3] [4] [5] 。由于晶界对于纳米材料的性能有显著的影响，而孪晶界作为一种共格晶界被引入在材料中，可以使材料表现出良好的力学稳定性和热稳定性。基于此，学者们已经对其展开了广泛的研究 [6] [7] [8] [9] [10] ，旨在揭示孪晶界对纳米金属材料变形机制的影响。

然而，用实验的方法分析原子间的相互作用存在着极大的挑战，而分子动力学模拟能够轻易追踪原子详细的运动轨迹，它能够分析位错滑移、晶界滑移等变形机制来解释实验结果。所以人们通过分子动力学开展了大量的相关研究的工作 [11] 。孙等人 [12] 利用MD模拟研究了孪晶厚度(TBS)对孪晶银纳米线的力学性能影响，结果表明：当TBS的倒数小于0.2 nm⁻¹时，位错在孪晶界上成核，此时孪晶界对材料起到弱化作用；当TBS的倒数大于0.2 nm⁻¹时，孪晶界阻碍位错的运动，此时孪晶界起到强化作用。Sun等人 [13] 研究了孪晶厚度对铜纳米线拉伸失效行为的影响，其研究表明：当孪晶界间距变化时，孪晶铜纳米线经历了三种不同的失效模式，其中包括韧性断裂、脆性断裂和韧脆转变。这取决于纳米线的长度，短的孪晶纳米线表现为韧性断裂，中间长度的表现为韧脆转变过程，长的表现为脆性断裂。Guo等人 [14] 基于分子动力学的方法研究孪晶界对金纳米线的影响时发现：随着孪晶间距的降低，发生了软化到强化的转变。虽然人们对于纳米孪晶材料做了大量的研究，但是纳米孪晶金属材料的微观变形机制仍不清晰。此外，当前关于纳米孪晶金属材料力学性能的研究主要针对于面心立方(fcc)结构，比如Cu、Ag、Ni等，关于体心立方(bcc)结构纳米孪晶金属力学性能的研究仍旧困乏 [15] ，对于纳米孪晶bcc结构金属材料变形机制的认识尚不完善，许多现象还缺少详细的解释。

为了进一步研究纳米孪晶bcc结构金属材料的变形机制，本文采用分子动力学方法研究带有孪晶结构的纳米多晶铁在拉伸载荷下的力学性能，主要讨论了孪晶界和温度对纳米多晶铁变形机理的影响，旨在揭示其微观的变形机制。

2. 建模与模拟

本文通过Voronoi方法构建了6个纳米多晶铁模型，其中包括1个不含孪晶界的模型和5个包含不同TBS孪晶界的模型。TBS分别为0.903 nm、1.66 nm、2.58 nm、3.54 nm和4.31 nm。每个纳米多晶铁模型都包含4个晶粒取向随机选取的二维柱状六边形晶粒，其晶粒尺寸为9.7 nm。坐标系采用x-[110]，y-[ 10]，z-[001]，模型的尺寸在X、Y和Z方向上分别为2.0 nm、15.6 nm和21.7 nm，原子总数大约为57,000个。图1 给出了纳米多晶铁的原子结构图，图中蓝色原子代表bcc结构，绿色原子代表fcc结构，白色原子则表示位错或者晶界等其他类型原子。本文选取的晶格常数为0.28553 nm [16] 。

在分子动力学模拟中，势函数的选取是至关重要的，因为其直接决定了模拟的结果的真实性和准确性。本文采用Ackland等人 [17] 发展的EAM势函数，这个势函数已经被证明能正确描述原子间的相互作用。系统的势能表示为：

$U={\displaystyle \underset{i}{\sum }{F}_i\left[{\displaystyle \underset{j}{\sum }\varphi \left(r_{ij}\right)}\right]}+{\displaystyle \underset{ij}{\sum }V\left(r_{ij}\right)}$

式中U表示材料的总能量， $F_i$ 为局部电子密度能量， ${\displaystyle {\sum }_j\varphi \left(r_{ij}\right)}$ 为其它原子的核外电子在原子 处产生的电子云密度之和， $V\left(r_{ij}\right)$ 为两原子之间的对势函数， $r_{ij}$ 为两原子之间的距离。

本文的模拟算法采用Verlet蛙跳法，它运用体系在 时刻的位置和加速度以及 $t-\delta t$ 时刻的位置，计算出 $t+\delta t$ 时刻的位置。该算法使用简单且占内存少，是分子动力学中最简单的算法。为了便于分析施加拉伸载荷后模型的结构变化，本文采用公共近邻分析方法(CNA) [18] 对原子进行着色，这些都是在可视化

Figure 1. Atomic structure diagram of initial model of nano-polycrystal iron

图1. 纳米多晶铁初始模型原子结构图

工具OVITO [19] 软件进行观测的。

本文研究了在300 K和10 K温度下，不同TBS的孪晶界对于纳米多晶铁的变形机制的影响。采用自主编制的C语言程序，在NPT系综下，先对初始模型进行15,000步的弛豫，使之能量最小化并且达到平衡状态；接着在X和Y方向保持零压的情况下，在Z方向上施加0.001的拉伸应变，然后系统弛豫300步以释放多余的应力使之回到平衡态。重复对模型施加位移载荷、弛豫，使之处于准静态受力状态。在这一过程中，模型的三个方向都采用周期性边界条件，时间步长为1 fs。

3. 模拟结果及分析

我们分别研究了温度为300 K和10 K时，孪晶厚度对于纳米多晶铁力学性能的影响。图2给出了不同TBS孪晶界模型和不包含孪晶界模型的应力应变曲线。从图2(a) 和图2(b)都可以观察到：在拉伸应力下，所有模型的应力都会随着应变的增加线性上升，随着应变进一步增加，应力达到某一个峰值，然后下降进入塑性变形阶段，此时应力波动变化。杨氏模量是应力–应变曲线在线性阶段的斜率，从图2(a) 和2(b)还可以看出，杨氏模量随着TBS的增大而增大。众所周知，在拉伸载荷前金属材料中加入的晶界或孪晶界会导致轻微的塑性变形，从而降低金属材料的力学性能 [20] ，纳米多晶铁杨氏模量随TBS的增大而增大，主要是因为TBS的增大使得孪晶界原子数占总原子数的比例减小。在图2(a)中，不含孪晶界的纳米多晶铁模型的峰值应力大约为7.58 GPa，而包含孪晶界的模型的峰值应力都低于7.58 GPa。在图2(b)中，不含孪晶界的纳米多晶铁模型的峰值应力大约为8.50 GPa，而包含孪晶界的模型的峰值应力都低于8.50 GPa。这说明在10 K和300 K温度下，纳米多晶铁内引入此范围内TBS的孪晶界，对模型都起到弱化的作用。此外，我们还可以观察到：在300 K时，TBS为1.66 nm的模型的流动应力相对来说比较平稳。

为了更好的说明温度和孪晶厚度对模型变形行为的影响，图3 给出了300 K和10 K时，纳米多晶铁峰值应力和1/TBS的关系。(图3(a) 表示温度为300 K时模型的峰值应力和1/TBS的关系，图3(b)表示温度为10 K时模型峰值应力和1/TBS的关系)。从图3(a)和图3(b)都可以看出：当TBS低于某一个临界值时，峰值应力和1/TBS成反比，也就是说，模型的峰值应力随着孪晶厚度的增大而增大，遵循反常的Hall-Petch关系。当TBS高于某一个临界值时，峰值应力和1/TBS成正比，即模型的峰值应力随着孪晶厚度的增大而减小，遵循Hall-Petch关系。在300 K和10 K温度下，该临界值分别为3.54 nm和1.66 nm，这说明临界值依赖于温度的变化，300 K的临界值大于10 K温度下对应的临界值。从图3(a)和图3(b)还可以观察到：包含孪晶界模型的峰值应力均低于不含孪晶界的模型的峰值应力，这也说明了在模型中引入孪晶界对模型起到弱化的作用。此外，对比图3(a)和图3(b)还可以看出：在相同TBS下，10 K温度下的模型的峰值应力均高于300 K温度下模型的峰值应力。这是因为随着温度的增加，原子的活动性增强，在拉伸过程中，原子更容易偏离平衡位置，因此所需要的拉伸应力相比于低温下更小。

为了揭示加入孪晶界对于纳米多晶铁的影响，我们主要研究了300 K时，不同TBS的纳米多晶铁的变形机理。图4给出了在温度为300 K下，TBS为1.66 nm的纳米多晶铁模型在拉伸应变分别为0.04、0.081、0.103、0.114和0.182的拉伸原子结构图(图4(a)~(e) 分别代表应变为0.04、0.081、0.103、0.144、0.182的拉伸原子结构图)。从图4(a)和图4(b) (圈中为孪晶胚成核)可以看出：当应变为0.081时，1号晶粒和2号晶粒相邻的晶界处有孪晶胚成核，孪晶胚形成孪晶带并且朝着相对的孪晶界处扩展。随着应变的增加，当应变达到0.103时，孪晶带与孪晶界相互作用，造成孪晶界处的应力集中，使得孪晶界成为萌生变形孪晶的源，从而在此孪晶界处又有新的孪晶胚成核进而形成孪晶带，然后扩展，如图4(c) 中2号晶粒圈中所示。随着应变的进一步增加，其他孪晶界处也有变形孪晶的形成。因此，孪晶界成为变形孪晶的成核源，对纳米多晶铁起弱化作用。此外，对比图4(a) 和图4(c)可以发现，4号晶粒中的孪晶厚度

Figure 2. The stress-strain curves of nano-polycrystal iron with different twin thickness and different temperatures ((a) 300 K, (b) 10 K)

图2. 不同孪晶厚度的纳米多晶铁的应力–应变曲线((a) 300 K温度，(b) 10 K温度)

明显变窄，这说明在拉伸过程中，孪晶界发生迁移的现象。这种迁移的现象是由于2个1/12 <111>不全位错在{112}孪晶面上按照箭头指向方向集体移动所引起的。如图4(f) 放大图所示，随着应变增大到0.114，孪晶界继续迁移，相邻孪晶界逐渐靠近，孪晶端部与晶界相交处由于非共格的结构，相较于共格的孪晶

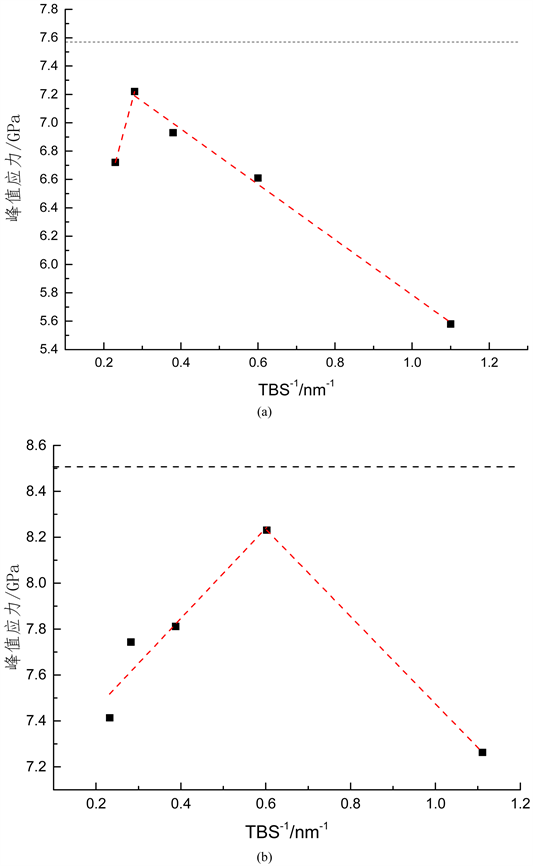
Figure 3. The relationship between peak stress of nano-polycrystal iron and 1/TBS at different temperatures ((a) 300 K, (b) 10 K)

图3. 不同温度下纳米多晶铁峰值应力与1/TBS的关系((a) 300 K温度，(b) 10 K温度)

界有更大的应力集中，有更高的可动性，随着应变的增大，孪晶端部从晶界处逐渐溶解到基体内部并最终消失 [21] [22] ，导致退孪晶的发生，此时局部晶格发生畸变，晶粒取向发生变化(图4(d)圈中为退孪晶端部)。当应变达到0.182时，可以看出，1号晶粒和2号晶粒的相邻的晶界处有裂纹成核的现象(图4(e)圈中所示)，并且1、2和3号晶粒原有的晶界大部分消失，晶粒发生合并。此外，本文利用位错提取算

Figure 4. The atomic structure diagram of model with TBS 1.66 nm at different strain and 300 K ((a) 0.04, (b) 0.081, (c) 0.103, (d) 0.114, (e) 0.188, (f) enlarged view of twin)

图4. 300 K时TBS为1.66 nm模型在不同应变下的原子结构图((a) 0.04, (b) 0.081, (c) 0.103, (d) 0.114, (e) 0.188, (f)孪晶放大图)

法分析了拉伸载荷下纳米多晶铁中位错的行为，研究发现在塑性变形过程中，晶界处位错成核向晶粒内扩展，晶粒内出现了1/2 <111>位错。因此可以得出：孪晶和位错的成核主要来自于晶界，这是因为晶粒内部缺少孪晶和位错成核的源。

为了进一步说明变形孪晶的形成机理，图5给出了变形孪晶的生成过程。从图5可以看出：1/6 <111>不全位错在晶界处成核，并且在其后端留下了一些堆垛层错，1/6 <111>不全位错的成核引起孪晶胚的成核。随着应变的增加，最初成核的1/6 <111>不全位错沿着<111>方向扩展。同时，额外的1/6 <111>不全位错又在堆垛层错和孪晶界的交界处产生，形成了两条{112}孪晶面。两条孪晶面又形成孪晶带，最终孪晶前端到达孪晶界处后湮灭。

我们同样研究了温度为10 K时，不同孪晶厚度的纳米多晶铁的拉伸力学性能。发现其变形机理与300 K时基本相同，同样为变形孪晶的生成和退孪晶的发生，同时伴有晶粒交界处沿晶裂纹的成核与扩展。表1给出了在300 K和10 K下，不同TBS的纳米多晶铁在裂纹成核时的临界应变。首先在300 K时，从表1中可以看出，不包含孪晶界的纳米多晶铁产生裂纹的临界应变为0.104。当纳米多晶铁引入孪晶界，并且TBS大于3.54 nm时，产生裂纹的临界应变为0.88，这说明该TBS的孪晶界削弱了纳米多晶铁的塑性。当TBS在0.903~3.54之间时，裂纹产生的临界应变均大于0.104，这说明该范围内的TBS的孪晶界对纳米多晶铁的塑性有增强的作用。特别是当TBS为1.66 nm时，此时模型产生裂纹的临界应变最大，也就是说，存在一个使其塑性最好的最佳TBS。从图2中的应力-应变曲线也可以看出，TBS为

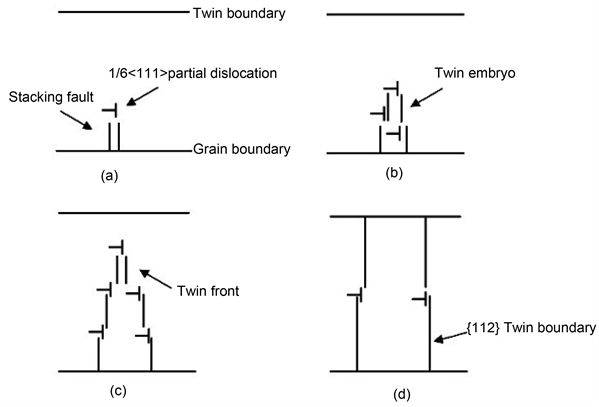
Figure 5. The growth process of deformation twins

图5. 变形孪晶的生长过程

Table 1. The critical strain of crack nucleation in nano-polycrystal iron with different twin thickness at 10 K and 300 K

表1. 10 K与300 K下不同孪晶厚度纳米多晶铁产生裂纹时的临界应变

1.66 nm的模型流动应力相对而言比较平缓。在10 K时，不含孪晶界的纳米多晶铁产生裂纹的临界应变为0.102，在引入孪晶界后发现其产生裂纹的临界应变均大于不含孪晶界的纳米多晶铁，这说明孪晶界在不同程度上提升了纳米多晶铁的塑性。这是因为孪晶界在变形过程中提供了更多塑性变形的场所，促进了变形的发生。而10 K时除孪晶厚度为4.31 nm模型产生裂纹的临界应变高于300 K时的临界应变，其余模型产生裂纹的临界应变普遍低于300 K的临界应变。这说明随着温度降低，其塑性也随之降低，因为相比于高温，材料中原子扩散能力减弱，变形能力降低，故其塑性比300 K时较差。

4. 结论

本文利用分子动力学的方法模拟了单向拉伸载荷下孪晶界和温度对纳米多晶铁力学性能的影响，模拟结果表明：引入孪晶能弱化纳米多晶铁，其杨氏模量随孪晶厚度的增大而增大，变形机制主要为孪晶界处变形孪晶的萌生与扩展。在孪晶厚度小于临界值时，其峰值应力随孪晶厚度的增大而增大，表现为反常的Hall-Petch关系。当孪晶厚度大于临界值时，峰值应力随着孪晶厚度的增大而减小，表现出Hall-Petch关系。温度为10 K时的临界值1.66 nm明显低于温度为300 K的临界值3.54 nm，这说明温度变化影响着临界值。孪晶的加入在不同程度上提升了纳米多晶铁的塑性。

基金项目

西安邮电大学研究生创新基金项目(No. 106-602080001)资助课题。