基于改进遗传算法的同步发电机参数辨识

Parameter Identification of Synchronous Generator Based on Improved Genetic Algorithm

摘要: 为解决系统小扰动情况下的同步发电机参数辨识问题，应用改进遗传算法进行计算。针对轮盘赌选择操作的随机性，通过改变选择方式，有效地规避了搜索后期易陷入局部最优的缺陷。以PMU实测数据为基础，选择改进Euler法求解微分方程，根据最小二乘原理构建目标函数，分别采用改进的遗传算法和粒子群算法进行辨识，比较了两种算法的优劣，辨识结果表明改进的遗传算法具有更高辨识精度。

Abstract: A genetic algorithm for the identification of synchronous generator parameters is proposed in the case of system minor disturbance. In view of the randomness of the operation of roulette, the selection method is improved, and the problem of local optimum is avoided effectively. In order to solve the differential equation, the improved Euler method is selected, and the objective function is built according to the application of least square principle, then the improved genetic algorithm and particle swarm optimization (PSO) used for the identification of synchronous generator parameters are identified which based on PMU measured data. The identification results which compare the ad-vantages and disadvantages of two kinds of algorithm show that the improved genetic algorithm has higher identification accuracy.

1. 引言

随着电网的规模和智能化水平的不断提高，电力系统的安全维护愈加成为广大电力从事者所关注的焦点。同步发电机是电力系统的核心元件，若同步发电机参数偏离实际，将严重影响电力系统的稳定性，因而，同步发电机的分析、控制、保护、运行均对其参数的准确性有着很高的要求。进而言之，同步发电机参数的准确辨识对电力系统的稳定运行分析有着极其重要的意义 [1] [2] [3] 。

同步发电机参数辨识的方法主要分为频域响应法和时域响应法 [4] [5] [6] [7] [8] [11] 。频域法虽然在数学原理上比较成熟，算法的稳定性好，但因其存在只可分析线性系统的短板，导致该方法无法处理发电机强耦合、非线性动态过程 [10] 。传统时域法中最常用的有最小二乘法和卡尔曼滤波法，但由于方法的收敛性与初值、权重因子等的选取密切相关，导致难以搜索到全局最优解 [9] [12] [13] 。基于GPS的同步相量测量技术的出现和PMU的大量安装与应用，获得电力系统动态数据变得方便而快捷，同时伴随着系统辨识理论的发展，根据在线测量数据进行系统参数辨识已经成为获取同步发电机参数的重要途径 [14] [15] [16] [17] 。上述方法的显著特点是：可考虑电机实际运行状况，一旦辨识成功，即能计及各种因素的效应，计算过程简单，且不用给出过多的假设条件，所得参数能很好地反映电机动态行为。由于大部分情况下的PMU数据为系统稳定运行或受到小扰动时的实测值，电机的暂态过程往往很难被充分激发，随着模拟进化类方法在电力系统辨识领域的应用，利用大量的小扰动数据反复进行试验，参数辨识的优化问题已得到较好的解决。鉴于进化策略法对参数的初值要求较高难以保证辨识的精确性，粒子群算法精度易于陷入局部最优而被降低，所以针对系统小扰动情况，需要提出更为有效的优化方法 [18] [19] 。本文为解决同步发电机在小扰动情况下的参数辨识问题，提出了经过改进后的遗传算法，通过改进选择过程，既提高了辨识的精确性，又避免了算法陷入局部最优的问题。

2. 同步发电机的数学模型

同步发电机参数的辨识需要首先建立其数学模型，选取合适的电压测量值作为输入，通过改进的遗传算法来寻找一组参数，使得经过模型计算得到的输出电流量和实测电流量的误差最小，此时对应的参数即为辨识出的参数。因此，选取合适的同步发电机数学模型是同步发电机参数辨识的重要前提。

同步发电机的实用参数数学模型在不同场合下有不同的选取原则，本文选用利于描述实心转子的六阶模型作为同步发电机的数学模型，此与实际运行发电机相一致。现对同步发电机六阶模型作出如下假设 [10] ：

1) 忽略定子磁暂态过程；

2) 计及转子d轴、q轴的暂态过程及次暂态过程。

根据上述假设，建立了以标幺值(时间常数除外)表示的同步发电机电气模型：

d轴模型

$\{\begin{array}{l}{T^{\prime }}_{\text{d}0}\cdot \frac{\text{d}{E^{\prime }}_{\text{q}}}{\text{d}t}=E_f-{E^{\prime }}_{\text{q}}-\frac{x_{\text{d}}-{x^{\prime }}_{\text{d}}}{{x^{\prime }}_{\text{d}}-{x^{″}}_{\text{d}}}\left({E^{\prime }}_{\text{q}}-{E^{″}}_{\text{q}}\right)\hfill \\ {T^{″}}_{\text{d}0}\cdot \frac{\text{d}{E^{″}}_{\text{q}}}{\text{d}t}={E^{\prime }}_{\text{q}}-{E^{″}}_{\text{q}}-\left({x^{\prime }}_{\text{d}}-{x^{″}}_{\text{d}}\right)i_{\text{d}}+{T^{″}}_{\text{d}0}\cdot \frac{\text{d}{E^{\prime }}_{\text{q}}}{\text{d}t}\hfill \\ \begin{array}{l}{u}_{\text{q}}={E^{″}}_{\text{q}}-{x^{″}}_{\text{d}}{i}_{\text{d}}\\ E_f=k\cdot u_{f\text{d}}\end{array}\hfill \end{array}$ (1)

q轴模型

$\{\begin{array}{l}{T^{\prime }}_{\text{q}0}\cdot \frac{\text{d}{E^{\prime }}_{\text{d}}}{\text{d}t}=-{E^{\prime }}_{\text{d}}-\frac{x_{\text{q}}-{x^{\prime }}_{\text{q}}}{{x^{\prime }}_{\text{q}}-{x^{″}}_{\text{q}}}\left({E^{\prime }}_{\text{d}}-{E^{″}}_{\text{d}}\right)\hfill \\ {T^{″}}_{\text{q}0}\cdot \frac{\text{d}{E^{″}}_{\text{d}}}{\text{d}t}={E^{\prime }}_{\text{d}}-{E^{″}}_{\text{d}}+\left({x^{\prime }}_{\text{q}}-{x^{″}}_{\text{q}}\right)i_{\text{q}}+{T^{″}}_{\text{q}0}\cdot \frac{\text{d}{E^{\prime }}_d}{\text{d}t}\hfill \\ u_{\text{d}}={E^{″}}_{\text{d}}+{x^{″}}_{\text{q}}{i}_{\text{q}}\hfill \end{array}$ (2)

式(1)、(2)中参数以d轴为例进行说明，其中k为电机内电势E_f与励磁电压u_fd的比例系数；u_d和i_d为d轴电压和电流；x_d为d轴同步电抗； ${x^{\prime }}_{\text{d}}$ 、 ${x^{″}}_{\text{d}}$ 、 ${T^{\prime }}_{\text{d0}}$ 、 ${T^{″}}_{\text{d0}}$ 、 ${E^{\prime }}_{\text{d}}$ 和 ${E^{″}}_{\text{d}}$ 是d轴暂态电抗、次暂态电抗、暂态开路时间常数、次暂态开路时间常数、暂态电势和次暂态电势。

3. 发电机参数辨识

由同步发电机的电气模型可知，电机的d轴、q轴解耦，所以可将d轴和q轴参数分开辨识。辨识时先计算稳态参数，再辨识暂态参数，流程见图1。

在稳态参数计算时，由d轴电压U_d和q轴电流I_q可计算q轴的同步电抗，即

$x_{\text{q}}=U_{\text{d}}/I_{\text{q}}$ (3)

根据隐极式的同步发电机特点，d轴同步电抗与q轴同步电抗近似相等，可取

$x_{\text{d}}=x_{\text{q}}$ (4)

3.1. 目标函数

在参数辨识过程中需要寻优，这就先要构造一个目标函数。由(1)、(2)可知，根据 $u_{\text{q}}={E^{″}}_{\text{q}}-{x^{″}}_{\text{d}}{i}_{\text{d}}$ 和 $u_{\text{d}}={E^{″}}_{\text{d}}-{x^{″}}_{\text{q}}{i}_{\text{q}}$ 可以得到d轴和q轴电流的设定值，通过辨识计算可得到d轴和q轴电流的计算值，应用最小二乘原理以电流实际值和辨识值的差值加权最小作为目标函数，d轴、q轴的目标函数建立如下：

$J_{\text{d}}={\displaystyle \underset{t=1}{\overset{n}{\sum }}{\left(i_{\text{dc}}-i_{\text{dm}}\right)}^2}$ (5)

$J_{\text{q}}={\displaystyle \underset{t=1}{\overset{n}{\sum }}{\left(i_{\text{qc}}-i_{\text{qm}}\right)}^2}$ (6)

其中，J_d和J_q分别为d轴和q轴模型的目标函数，i_dc和i_qc分别为根据d轴、q轴的辨识参数计算出的电流值，i_dm和i_qm是根据PMU数据通过Park变换处理后的d轴、q轴电流实测值。

本文在用遗传算法寻优时，并不采用上述的目标函数，而是对目标函数进行变换。这里采用了遗传

算法的适应度函数F_d和F_q，现以d轴为例说明：目标函数J_d之值越接近于零，则辨识效果越好，而适应度函数F_d的构建则以选择较大的适应度值为原则，以便于参数寻优。因此，参数辨识中为了将辨识原理与优化方法联系起来，可取目标函数倒数当作适应度函数，即F_d = 1/J_d (J_d不为0)。

3.2. 微分方程的求解

以PMU数据处理后的实测d轴电压u_d、q轴电压u_q、励磁电压u_fd作为输入量，求解d轴电气模型(1)、q轴电气模型(2)中的微分方程中的4个状态变量，最终得到d轴电流i_d、q轴电流i_q。

解方程时选用具有四阶精度的改进Euler法，先利用Euler公式求得一个初步的近似值 ${\bar{y}}_{n+1}$ ，称之为预测值，预测值 ${\bar{y}}_{n+1}$ 的精度相对较差，再用梯形公式将其校正一次，得到 $y_{n+1}$ ，这个结果称为校正值，这样建立的预测——校正方法通常称为改进的Euler法，改进Euler法的示意图如图2所示。

${\bar{y}}_{n+1}=y_n+hf\left(x_n,y_n\right)$ (7)

$y_{n+1}=y_n+\frac{h}{2}\left[f\left(x_n,y_n\right)+f\left(x_{n+1},{\bar{y}}_{n+1}\right)\right]$ (8)

4. 优化算法

遗传算法(GA)是一种借鉴生物界自然选择可实现全局并行优化的搜索工具 [20] 。GA具有应用广泛、鲁棒性强和适于并行分布处理的特点。GA的原理是从随机解出发，在每次迭代中搜索最优解，并利用适应度来评价解的品质，通过优胜劣汰的自然选择机制搜索每一代的最优值最终得到全局最优。

遗传算法不同于传统的进化类法，主要步骤包括：选择、交叉和变异，其中交叉和变异是遗传算法的主要部分，即待寻优参数通过按照一定的交叉概率和变异概率产生新个体。本文设置算法的交叉概率为0.6，设置变异概率为0.02 [20] 。由于辨识过程d轴和q轴解耦，因此优化算法的应用以d轴参数为例，首先根据

Figure 1. Synchronous generator parameter identification

图1. 同步发电机参数辨识流程

Figure 2. Improved Euler method

图2. 改进Euler法

稳态数据计算得出稳态参数，然后将稳态参数代入暂态辨识过程。暂态辨识中待辨识的暂态参数有： ${x^{\prime }}_{\text{d}\left(\text{p}\text{.u}\right)}$ 、 ${x^{″}}_{\text{d}\left(\text{p}\text{.u}\right)}$ 、 ${T^{\prime }}_{\text{d}0}\left(s\right)$ 和 ${T^{″}}_{\text{d}0}\left(s\right)$ ，辨识过程以d轴电压u_d和励磁电压u_fd作为模型的输入值，以d轴电流i_d为输出值。

考虑到待辨识参数的计算量问题，决定对待辨识参数的初值进行浮点数编码。为了克服算法在搜索后期效率低和易于收敛的缺点，因此本文对该算法的选择算子进行了改进：放弃轮盘赌选择方法，先对待辨识参数初值在有意义的辨识区域内进行随机设置，先计算个体的适应度，然后对个体适应度的大小进行排序，以平均适应度为阈值，选择适应度值大于平均适应度值的个体，并以最高适应度值为模板，选择不同模板的个体组成群体，直至到达种群规模。寻优时搜索到的每一组参数，都要代入d轴电气模型(1)中，并使用改进的Euler法求解d轴电流的辨识值，通过设置合理的迭代次数，即可得到最终的最优值。程序验证时发现：迭代次数过大并不会使辨识结果的精度更高，反而会增加辨识的计算时间，所以迭代次数设置在300上下即可得到为理想的辨识效果。改进遗传算法的流程图如图3所示。

5. 算例分析验证

以PMU在线记录的小扰动数据为基础，使用同步发电机六阶数学模型，选用具有四阶精度的改进Euler法求解电机微分方程，应用最小二乘原理构建模型的目标函数。之后分别采用粒子群算法(PSO)和改进的遗传算法(AGA)进行同步发电机参数辨识，以比较粒子群算法和改进遗传算法的优劣性。

本文基于华北电网PMU所测得的实际数据。选取内蒙古托克托电厂一号机组2010年4月14日上午10点47分的实际数据，我们截取扰动发生的42秒至46秒这个时间段，机端正序电压、正序电流和励磁电压的波形如图3所示。

之后分别采用粒子群算法和改进的遗传算法对PMU实测数据进行辨识验证，得到的辨识结果如下：其中表1和表2为两种优化算法的d轴、q轴参数辨识的结果比较。图4~图7为使用两种优化算法进行

Figure 3. AGA flow-process diagram

图3. 改进遗传算法流程简示

Figure 4. Waveform of PMU measured data

图4. 实测数据波形

Figure 5. Current fitting curve of direct axis-PSO

图5. d轴电流拟合曲线图–粒子群算法

Figure 6. The current fitting curve of direct axis-AGA

图6. d轴电流拟合曲线图–改进遗传算法

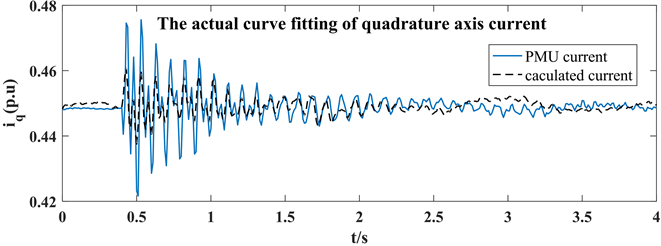
Figure 7. Current fitting curve of quadrature axis-PSO

图7. q轴电流拟合曲线图–粒子群算法

参数辨识得到的d轴、q轴的电流拟合曲线。

从图5~图8的拟合曲线的拟合效果可以看出，改进的遗传算法对电流曲线的拟合效果相比于粒子群

Figure 8. Current fitting curve of quadrature axis-AGA

图8. q轴电流拟合曲线图–改进遗传算法

Table 1. Comparison of identification result-direct axis

表1. 辨识结果比较-d轴

Table 2. Comparison of identification results-quadrature axis

表2. 辨识结果比较-q轴

算法要更加理想；表1和表2中的参数辨识结果表明，改进遗传算法由于全局寻优能力强，且规避了陷入局部最优的问题，使得搜寻出的同步发电机的参数与实际值更加接近，辨识误差更小；且计算得到的目标函数在数量级上远小于粒子群算法，辨识过程的精度更高。

6. 结论

本文以提出更好的同步发电机参数辨识的优化方法为目的，对于传统的遗传算法，针对选择操作的随机性，放弃了轮盘赌选择方法，并改进了选择方法，有效地规避了算法在搜索后期易陷于局部最优的问题。以PMU量测数据为基础，分别用粒子群算法和改进的遗传算法进行同步发电机参数辨识，并对两种优化算法的结果进行对比，参数辨识结果显示了改进的遗传算法更为有效且具更高的精度。改进的遗传算法不仅可以应用于电力系统参数辨识领域，同样可应用于其他的优化问题。