基于均匀化混沌系统的S-Box生成算法

Algorithm of Generating S-Box Based on Uniform Chaotic System

摘要: 该文给出了一个新的二次多项式混沌系统，并基于系统的概率密度函数对其进行均匀化处理。基于均匀化后的混沌系统构造了新的S-Box生成算法。对生成的S-Box进行性能检测，包括双射特性，非线性度，差分概率(DP)和线性概率(LP)分析，结果表明本文均匀化后混沌系统产生的S-Box具有较好的密码特性，适合用于加密系统。

Abstract: In this paper, a new quadratic polynomial chaotic system is given and homogenized based on its probability density function. Then, based on the homogenized chaotic systems, an S-box generation algorithm is constructed. The security of S-box is tested by numerical simulation including differential probability analysis and linear probability analysis. The statistical results show that the uniform chaotic system can produce better performance of S-boxes.

1. 引言

混沌是非线性动力学系统特有的一种无周期的有序运动。文献 [1] 中首次用数学定义描述了混沌一词。混沌系统具有高度的初值敏感性、伪随机性和不可预测性，使其在混沌密码学的研究中成为热点。自20世纪80年代以来，密码学家不断挖掘出了混沌在密码学领域中的应用潜力 [2] [3] [4] 。除此之外，混沌还在各个领域中得到广泛关注与应用。

为满足安全保密通信的要求，科学家往往希望得到均匀性随机性良好的随机数源。混沌系统作为重要的随机数源，在构造伪随机数发生器时，大部分系统不能满足均匀性要求。因此，找到有效的混沌系统均匀化方法有着重要的学术意义。文献 [5] 把混沌系统生成的序列通过反正切和反余弦函数变换成服从均匀分布的伪随机序列，文献 [6] 基于计算机浮点数表示，给出了将混沌序列变换成均匀伪随机序列的bit位操作方法，文献 [7] 曹光辉等人给出了一个基于概率原理将Logistic混沌系统产生的非均匀分布随机变量转化为服从均匀分布的随机变量的方法。

通过混沌映射的概率密度函数可以发现大部分混沌序列不服从均匀分布。混沌系统具有各态历经的特性，利用混沌映射的概率密度可以描述系统长期的统计特征。由于大多数混沌系统的复杂性，其概率密度函数并不容易获得。何振亚等人 [8] 通过证明Logistic映射与Tent映射的拓扑共轭关系以及Chebyshev映射与Tent映射的拓扑共轭关系，得到了Logistic映射和Chebyshev映射的概率密度。

一个 $n\times m$ 的S-Box是将n位输入映射到m位输出的非线性映射，由于S-Box是AES等分组密码中唯一的非线性部件，设计好的分组密码算法就很大程度上依赖于S-Box的性能。密码学研究者提出了很多构造动态S-Box的方法 [9] ，其中，将具有良好伪随机性的混沌系统用于构造动态S-Box便是一种重要方法 [10] 。

本文基于已有定理提出了一个新的二次多项式混沌系统，并基于拓扑共轭理论推出了混沌系统的概率密度函数，从而对系统进行修正，使其能够产生均匀化的随机序列；利用均匀化的混沌序列构造S-Box，对S-Box的性能指标进行统计分析，结论是均匀化后系统产生的S-Box密码性能良好。

本文其余部分安排如下：在第2节中提出了一个新的混沌系统，并基于概率密度函数对系统进行了均匀化处理。在第3节中，设计了一个动态S-Box的生成方法，利用均匀化后的混沌系统生成S-Box，并进行了S-Box性能分析。第4节总结全文。

2. 二次多项式混沌系统的均匀化处理

纸型

文献 [11] 提出了一般非线性二次多项式3-周期点存在的充分必要条件，表述为如下引理：

引理1 [11] ：二次多项式 $f\left(x\right)=a{x}^2+bx+c$ 有实的3-周期点的充要条件是

$b^2-4ac-2b\ge 7$

基于引理1，本文构造了新的一维混沌系统为：

$f\left(x\right)=1.28x^2+0.56x-1.72,x\in \left[-\frac{57}{32},\frac{43}{32}\right]$ (1)

将系统表示为

$x\left(n+1\right)=a{x}^2\left(n\right)+bx\left(n\right)+c$ (2)

其中

$a=1.28,b=0.56,c=-\mathrm{1.72.}$

图1(a)为混沌系统(2)随参数 $a\in \left[0.28,1.28\right]$ 变化的分岔图，其中参数 $b=0.56,c=-1.72$ ，图1(b)，图1(c)分别为混沌系统(2)随参数 $b,c$ 变化的分岔图，其中 $b\in \left[0.56,1.4\right]$ ， $c\in \left[-1.72,-0.72\right]$ 。

根据文献 [12] 中拓扑共轭的定义，如果存在一个可逆映射 $h:X\to Y$ ，使得 $h\left(g\left(x\right)\right)=f\left(h\left(x\right)\right)$ 成立，则称映射 $g\left(x\right)$ 和 $f\left(y\right)$ 是拓扑共轭的。以下证明混沌系统

$f\left(x\right)=1.28x^2+0.56x-1.72,x\in \left[-\frac{57}{32},\frac{43}{32}\right]$

与Tent映射是拓扑共轭的。

此处，Tent映射为

$g\left(x\right)=\{\begin{array}{l}2x,0\le x\le \frac{1}{2}\\ 2-2x,\frac{1}{2}\le x\le 1\end{array}$

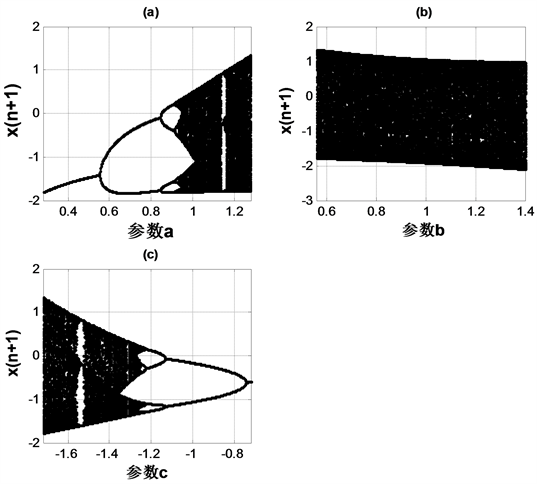
Figure 1. (a) The bifurcation diagram of parameter a in system (2); (b) The bifurcation diagram of parameter b in system (2); (c) The bifurcation diagram of parameter c in system (2)

图1. (a) 系统(2)关于参数a的分岔图；(b) 系统(2)关于参数b的分岔图；(c) 系统(2)关于参数c的分岔图

令连续可逆函数

$h\left(x\right)=\frac{25}{16}\cos \text{π}x-\frac{7}{32},x\in \left[0,1\right]$

则有

$\begin{array}{c}h\circ g\left(x\right)=\{\begin{array}{l}\frac{25}{16}\cos 2\text{π}x-\frac{7}{32},0\le x\le \frac{1}{2}\\ \frac{25}{16}\cos \text{π}\left(2-2x\right)-\frac{7}{32},\frac{1}{2}\le x\le 1\end{array}\\ =\frac{25}{16}\cos 2\text{π}x-\frac{7}{32}\\ =h(2x)\end{array}$

且

$\begin{array}{c}f\circ h\left(x\right)=\frac{32}{25}{h}^2\left(x\right)+\frac{14}{25}h\left(x\right)-\frac{43}{25}\\ =\frac{32}{25}{\left(h\left(x\right)+\frac{7}{32}\right)}^2-\frac{57}{32}\\ =\frac{32}{25}{\left(\frac{25}{16}\cos \text{π}x\right)}^2-\frac{57}{32}\\ =\frac{25}{16}\cos 2\text{π}x-\frac{7}{32}\\ =h(2x)\end{array}$

即 $h\left(g\left(x\right)\right)=f\left(h\left(x\right)\right)$ ， $f\left(x\right)$ 与Tent映射关于 $h\left(x\right)$ 拓扑共轭。

基于函数的共轭关系，可以证明混沌系统

$f\left(x\right)=1.28x^2+0.56x-1.72,x\in \left[-\frac{57}{32},\frac{43}{32}\right]$

的概率密度函数为

$\rho \left(x\right)=\{\begin{array}{l}\frac{1}{\text{π}}\frac{32}{\sqrt{2451-448x-1024x^2}}\text{,}x\in \left[-\frac{57}{32},\frac{43}{32}\right]\\ 0,其他\end{array}$

证明：已知Tent映射的概率密度函数为

${\rho }_T\left(x\right)=1,x\in \left(0,1\right).$

根据上述证明过程， $f\left(x\right)=1.28x^2+0.56x-1.72$ 与Tent映射关于 $h\left(x\right)=\frac{25}{16}\cos \text{π}x-\frac{7}{32}$ 拓扑共轭，因此有

$\begin{array}{c}{\rho }_f\left(x\right)={\rho }_T\left(h^{-1}\left(x\right)\right)\left|\frac{\text{d}{h}^{-1}\left(x\right)}{\text{d}x}\right|\\ =\frac{1}{\text{π}}\frac{32}{\sqrt{2451-448x-1024x^2}}\end{array}$

显然，系统(1)的概率密度函数表明该系统会生成不均匀的序列，容易具有明显的统计特性，不适合作为伪随机数发生器，不利于推广应用。以下基于概率密度函数，提出一个以系统(1)函数值为变量的反正弦函数，并证明该函数能够产生服从均匀分布的混沌序列。

定理1：已知随机变量X服从概率密度函数

$\rho \left(x\right)=\{\begin{array}{l}\frac{1}{\text{π}}\frac{32}{\sqrt{2451-448x-1024x^2}}\text{,}x\in \left[-\frac{57}{32},\frac{43}{32}\right]\\ 0,其他\end{array}$

则随机变量

$Z=\frac{1}{\text{π}}\arcsin \left(-\frac{16}{25}X-\frac{7}{50}\right)$ (3)

在区间 $\left[-\frac{1}{2},\frac{1}{2}\right]$ 上服从均匀分布。

证明：随机变量Z的分布函数

$\begin{array}{c}{F}_Z\left(z\right)=P\left(Z\le z\right)=P\left(\frac{1}{\text{π}}\arcsin \left(-\frac{16}{25}X-\frac{7}{50}\right)\le z\right)\\ ={\displaystyle {\int }_{-\infty }^{-\frac{25}{16}\sin \text{π}z-\frac{7}{32}}{\rho }_X\left(x\right)\text{d}x}\end{array}$ (4)

对式(4)求导，得到Z的概率密度

${\rho }_Z\left(z\right)=\{\begin{array}{c}1,-\frac{1}{2}\le z\le \frac{1}{2};\\ 0,其它.\end{array}$

综上，随机变量 $Z=\frac{1}{\text{π}}\arcsin \left(-\frac{16}{25}X-\frac{7}{50}\right)$ 在区间 $\left[-\frac{1}{2},\frac{1}{2}\right]$ 上服从均匀分布，由于随机变量Z与随机

变量X为一一对应关系，因此生成序列为混沌序列。

以上定理提出了利用概率密度函数对混沌系统进行均匀化处理的方法。由证明过程可知，经由(3)式把原二次多项式混沌系统(1)转换为服从均匀分布的随机变量。本文把式(2) (3)合称为修正的混沌映射，表示为

$\{\begin{array}{l}x\left(n+1\right)=1.28x{\left(n\right)}^2+0.56x\left(n\right)-1.72\\ z\left(n+1\right)=\frac{1}{\text{π}}\arcsin \left(-\frac{16}{25}x\left(n+1\right)-\frac{7}{50}\right)\end{array}$ (5)

针对均匀化前混沌系统式(1)和均匀化后系统式(5)产生的序列进行直方图统计，验证均匀化方法的有效性。图2(a)是原二次多项式系统生成混沌序列的频率直方图，图2(b)是修正混沌映射生成的具有均匀分布随机序列的频率直方图。由模拟结果对比可见，处理后的混沌序列均匀性明显增强。

3. 基于均匀化混沌系统构造S-Box

3.1. S-Box算法构造

S-Box作为分组密码中的非线性部件，主要起到置换的功能。为了达到更好的置乱效果，增加加密方案的抵抗攻击能力，本文利用混沌系统进行迭代，并基于混沌系统的不同的初始值动态生成 $8\times 8$ 的S-Box，因而，S-Box的密钥由混沌系统的参数，迭代次数，初值等构成。具体的算法步骤为：

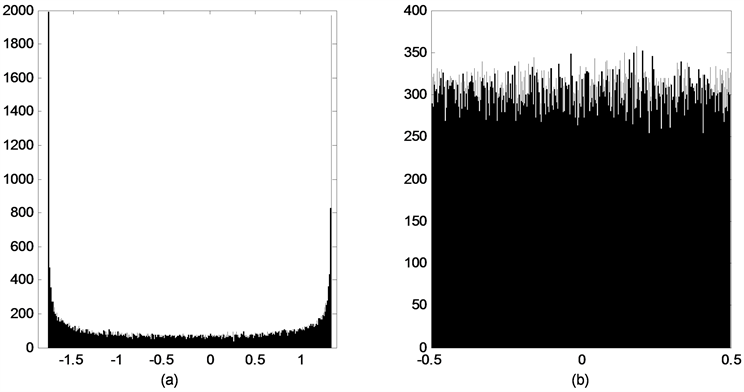
Figure 2. Histogram: (a) Histogram of the sequence before uniformity; (b) Histogram of the sequence after uniformity

图2. 统计直方图：(a) 均匀化前序列；(b) 均匀化后序列

1) 将相空间 $\left[-0.5,0.5\right]$ 进行n等分，分别为每个小区间标号为 $i=0,1,\cdots ,n$ ；

2) 取初值 $x_0$ ，利用混沌系统(5)式迭代n次，得到一个n维混沌序列；

3) 将序列值对应到相空间 $\left[-0.5,0.5\right]$ 中的相应小区间，用区间标号 $i\left(\mathrm{mod}256\right)$ ，得到一个n维位置序列；

4) 位置序列中前256个不相等的值依次构成S-Box序列。

当混沌迭代的初始值 $x_0$ 或迭代次数发生改变时，由于混沌系统的初值敏感性和不可预测性，算法相当于一个一次一密的加密部件。

3.2. S-Box性能分析

下面从动态生成的S-Box中选取出一个样本分析密码学性能指标，与现有混沌S-Box作比较分析，证明本文构造的由均匀化混沌系统生成的S-Box适用于设计分组密码方案。表1为选取的S-Box序列样本。

首先对双射特性进行检测，表1中S-Box样本的8个分量布尔函数记为

$$ ，线性运算之和都为128，与理想值相同，满足双射特性，输

出函数的比特平衡性很好。

S-Box的非线性度为 $N_s=\underset{\begin{array}{l}l\in L_n\\ 0\ne u\in F_2^m\end{array}}{\min }{d}_H\left(u\cdot S\left(x\right),l\left(x\right)\right)$ 。式中： $u\cdot S\left(x\right)$ 表示u与 $S\left(x\right)$ 的点积。表示全体n元线性和仿射函数之集； $d_H\left(x,y\right)$ 表示x和y的汉明距离。函数的非线性度越大，意味着抵抗线性

攻击的能力越强。表2给出了S-Box的8个布尔函数的非线性度，对比可见，表1的S-Box样本非线性度处在较高水平，表明更能够抵抗最佳线性逼近攻击。

S-Box的差分概率(DP)用来评价其抵抗差分密码攻击的能力，DP值越小，抵抗能力越强。而线性概率(LP)评价了S-box抵抗线性密码攻击的能力，LP 指标越小，抵抗效果越好。离散混沌S-Box的Lyapunov指数 [13] 可以用来衡量双射映射中自变量改变一比特时，映射值变化比特的情况。Lyapunov指数越大，说明自变量能够引起状态值的变成程度越高，意味着系统混沌性越好。本文构造S-Box的DP，LP及其Lyapunov指数结果与文献中S-Box的对比见表3。由对比结果可见，本文S-box的DP值和LP值均小于

Table 1. S-box sequence sample

表1. S-box序列样本

Table 2. Comparison of the nonlinearity of S-boxes

表2. S-Boxes的非线性度对比

Table 3. Comparison of the DP, LP, Lyapunov exponent of S-boxes

表3. S-Boxes的DP，LP，Lyapunov指数对比

文献 [14] [15] 中S-boxes的相应指标值，说明有均匀化系统构造的S-box可以更好地抵抗差分密码攻击和线性密码攻击。而Lyapunov指数比文献 [15] [16] 中S-boxes的Lyapunov指数来得小，说明本文S-box的混沌程度还有待提高。

4. 结论

本文提出了一个新的二次多项式混沌系统，结合拓扑共轭理论和tent映射的概率密度函数推出了系统的概率密度函数，并基于概率原理提出了一个满足均匀化分布的随机变量。利用均匀化前后系统生成的混沌序列的直方图统计直观地说明了均匀化效果良好。基于均匀化后混沌系统设计了一个新的构造S-Box的算法，对S-Box样本进行各项指标分析对比可见，该算法能够产生密码性良好的S-Box，对差分密码攻击和线性密码攻击的抵抗能力较强。但是，由均匀化系统构造出来的S-box在混沌程度上稍逊一筹，具体原因可能有两方面，一方面是由于均匀化方法导致混沌系统的混沌性受到影响，另一方面是S-box生成算法的不足，未来的研究将从这两方面进行改进，致力于为进一步设计分组密码算法提供良好的非线性资源。