求解基于l_p+l₂范数问题的共轭梯度法

Conjugate Gradient Method for l_p+l₂ Norm Problems

摘要: 本文针对稀疏信号的重构问题提出新的函数模型，通过光滑化绝对值函数光滑我们的模型，基于三项共轭梯度法对稀疏信号进行恢复，并试验了不同参数值对稀疏信号恢复效果的影响，数值实验表明本文算法的数值有效性。

Abstract: A new model is proposed for sparse signal reconstruction. We smooth our model by smoothing absolute value function. Then we use a new tri-term conjugate gradient method to restore sparse signal. The effect of different parameters on sparse signal recovery is tested. The numerical results show that our algorithm is efficient.

1. 引言

压缩感知技术在信号重构问题中有着广泛的应用，而稀疏性是压缩感知中的重要问题。2006年，E. Candes，J. Romberg和T. Tao在文献 [1] 中提出，若矩阵A满足RIP条件，则可以通过下述模型(1)精确恢复信号：

$\underset{x\in R^n}{\min }{\Vert x\Vert }_0,\text{s}\text{.t}.Ax=b.$ (1)

其中 $A\in R^{m\times n}\left(m<n\right)$ 为观测矩阵， $b\in R^m$ 为原始信号， ${\Vert x\Vert }_0$ 表示0范数，即稀疏信号x中非零元素的个

数。但该问题是NP-hard问题 [2] ，因此学者们考虑了如下的凸优化问题：

$\underset{x\in R^n}{\min }{\Vert x\Vert }_1,\text{s}\text{.t}.Ax=b.$ (2)

(2)称作1范数模型，在适当的假设下，由文献 [3] 的定理1.3可知，模型(2)可以较精确地恢复原始信号。

由于问题(2)的凸性，有许多有效算法可求解之，如基追踪法 [4] ，迭代阈值方法 [5] 。近年来，p ( $0<p<1$ )拟范数模型受到学者们的青睐，因p范数较1范数更能得到稀疏解，尤其是徐宗本提出p = 0.5时具有较好的计算效果 [6] 。p范数模型为：

$\underset{x\in R^n}{\min }{\Vert x\Vert }_{\text{p}},\text{s}\text{.t}.Ax=b.$ (3)

由于 $0<p<1$ ，故问题(3)为非凸问题，且与0范数同样是NP-hard问题。文献 [1] 中作者利用光滑逼近 $\left|\cdot \right|$ 函数进而光滑逼近p范数。受到该文的启发，本文利用文献 [7] [8] 中的光滑逼近 $\left|\cdot \right|$ 函数技术光滑逼近p范数，且结合p范数与2范数各自的优点，利用p范数与2范数加权的方法弥补由于p过小而引起的数值不稳定，从而应用共轭梯度法进行信号恢复，并在适当的假设下，证明了算法的全局收敛性，同时进行了数值测试，测试结果证明我们的方法是有效的。

2. 模型及其性质

我们考虑如下模型：

$\underset{x\in R^n}{\min }{\lambda }_1{\Vert x\Vert }_p+{\lambda }_2{\Vert x\Vert }_2,\text{s}\text{.t}.Ax=b.$

其中 ${\lambda }_{\text{1}},{\lambda }_{\text{2}}\in R$ 。该问题的正则化问题为：

$\underset{x\in R^n}{\min }{\lambda }_1{\Vert x\Vert }_p+{\lambda }_2{\Vert x\Vert }_2+\frac{1}{2}{\Vert Ax-b\Vert }_2^2.$ (4)

其模型较p范数模型(3)，加入了一项2范数项进行调节p过小时目标函数的非凸程度，以p = 0.3时为例，依次做 $R={\lambda }_2/{\lambda }_1=0,1,10,100$ 时的范数图像，如图1至图4所示：

Figure 1. R = 0 norm image

图1. R = 0范数图像

Figure 2. R = 1 norm image

图2. R = 1范数图像

Figure 3. R = 10 norm image

图3. R = 10范数图像

Figure 4. R = 100 norm image

图4. R = 100范数图像

可见通过适当调整 ${\lambda }_{\text{1}},{\lambda }_{\text{2}}$ 取值在保证产生稀疏解的同时可以增强问题的凸性。由p范数的定义 ${\Vert x\Vert }_p={\left({\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left|x_i\right|}^p}\right)}^{\frac{1}{p}}$ 可知，由于 $\left|x\right|$ 的非光滑性，导致 ${\Vert x\Vert }_p$ 是非光滑的，因而我们通过光滑绝对值函数 $\left|x\right|$ 对 ${\Vert x\Vert }_p$ 进行光滑逼近。文献 [8] 中对绝对值函数提出如下两个光滑函数：

${\phi }_{\text{1}}\left(\epsilon ,t\right)=\{\begin{array}{l}t,t\ge \frac{\epsilon }{2},\\ \frac{t^2}{\epsilon }+\frac{\epsilon }{4},-\frac{\epsilon }{2}<t<\\ -t,t\le -\frac{\epsilon }{2}.\end{array}\frac{\epsilon }{2}$ 及 ${\phi }_{\text{2}}\left(\epsilon ,t\right)=\{\begin{array}{l}\frac{t^2}{2\epsilon },\left|t\right|\le \epsilon ,\\ \left|t\right|-\frac{\epsilon }{2},\left|t\right|>\epsilon .\end{array}$ (5)

利用 ${\phi }_i\left(i=1,2\right)$ ，我们得到的模型为：

$\min {\lambda }_1{\varphi }_i\left(\epsilon ,x\right)+{\lambda }_2{\Vert x\Vert }_{2,\mu }+\frac{1}{2}{\Vert Ax-b\Vert }_2^2.$ (6)

其中，

${\varphi }_i\left(x\right)={\left[{\displaystyle \underset{j=1}{\overset{n}{\sum }}{\phi }_i{\left(\epsilon ,x_j\right)}^p}\right]}^{\frac{1}{p}},i=1,2,$ (7)

${\Vert x\Vert }_{2,\mu }=\sqrt{x_1^2+x_2^2+\cdots +x_n^2+{\mu }^2},\mu >0.$

为叙述方便，令：

$G_i\left(x\right)={\lambda }_1{\varphi }_i\left(\epsilon ,x\right)+{\lambda }_2{\Vert x\Vert }_{2,\mu }+\frac{1}{2}{\Vert Ax-b\Vert }_2^2,\left(i=1,2\right).$ (8)

计算函数 $G_i\left(x\right)$ 的梯度：

$\nabla G_i\left(x\right)={\lambda }_1\nabla {\varphi }_i\left(\epsilon ,x\right)+{\lambda }_2\nabla {\Vert x\Vert }_{2,\mu }+A^{\text{T}}\left(Ax-b\right).$ (9)

引理1 设D为 $R^n$ 中的紧集，若 $h:D\to R$ 是D上的光滑函数，则h在D上满足Lipschitz条件，即：

$\Vert h\left(x\right)-h\left(y\right)\Vert \le L\Vert x-y\Vert ,\forall x,y\in D.$

其中 $L>0$ 称为Lipschitz常数。

证明：对 $\forall x,y\in D$ ，由 $h\left(x\right)$ 的光滑性及Lagrange中值定理可知：

$\left|h\left(x\right)-h\left(y\right)\right|=\left|\nabla h^{\text{T}}\left(\xi \right)\left(x-y\right)\right|\le \Vert \nabla h\left(\xi \right)\Vert \cdot \Vert x-y\Vert$ ，其中 $\xi$ 位于 $x,y$ 之间。

因D为紧集，则 $\exists L>0$ ， $\Vert \nabla h\left(\xi \right)\Vert \le L$ ，从而 $\Vert h\left(x\right)-h\left(y\right)\Vert \le L\Vert x-y\Vert$ 。

引理2设 $D\subset R^n$ 为紧集， $f,g:D\to R$ 在D上Lipschitz连续，则 $f\cdot g$ 在D上Lipschitz连续。

证明：因D紧且f和g均在D上Lipschitz连续，则 $\exists M>0,\forall L_1>0,L_2>0$ ，满足：

$\left|f\left(x\right)\right|\le M,\left|g\left(x\right)\right|\le M,\left|f\left(x\right)-f\left(y\right)\right|\le L_1\Vert x-y\Vert ,\left|g\left(x\right)-g\left(y\right)\right|\le L_2\Vert x-y\Vert ,\forall x,y\in D.$

对 $\forall x,y\in D$ ，有：

$\begin{array}{l}\left|f\left(x\right)g\left(x\right)-f\left(y\right)g\left(y\right)\right|\\ =\left|f\left(x\right)g\left(x\right)-f\left(y\right)g\left(x\right)+f\left(y\right)g\left(x\right)-f\left(y\right)g\left(y\right)\right|\\ \le \left|g\left(x\right)\right|\left|f\left(x\right)-f\left(y\right)\right|+\left|f\left(y\right)\right|\left|g\left(x\right)-g\left(y\right)\right|\\ \le M{L}_1\Vert x-y\Vert +M{L}_2\Vert x-y\Vert \\ =M\left(L_1+L_2\right)\Vert x-y\Vert .\end{array}$

引理3 若 ${\phi }_i\left(i=1,2\right)$ 由(5)定义，则 ${{\phi }^{\prime }}_i\left(\epsilon ,t\right)$ 在紧集D上Lipschitz连续。

证明：对于 $i=1$ 的情况，我们有：

${{\phi }^{\prime }}_i\left(\epsilon ,t\right)=\{\begin{array}{l}\mathrm{sgn}\left(t\right),\left|t\right|\ge \frac{\epsilon }{2},\\ \frac{2t}{\epsilon },\left|t\right|<\frac{\epsilon }{2}.\end{array}$

当 $\frac{\epsilon }{2}>t_1>t_2>-\frac{\epsilon }{2}$ 时，有：

$\left|{{\phi }^{\prime }}_1\left(\epsilon ,t_1\right)-{{\phi }^{\prime }}_1\left(\epsilon ,t_2\right)\right|\le \left|\frac{2t_1}{\epsilon }-\frac{2t_2}{\epsilon }\right|=\frac{2}{\epsilon }\left|t_1-t_2\right|.$

当 $t_1>\frac{\epsilon }{2}>t_2>-\frac{\epsilon }{2}$ 时，有：

$\left|{{\phi }^{\prime }}_1\left(\epsilon ,t_1\right)-{{\phi }^{\prime }}_1\left(\epsilon ,t_2\right)\right|=\left|1-\frac{2t_2}{\epsilon }\right|<\left|\frac{2t_1}{\epsilon }-\frac{2t_2}{\epsilon }\right|=\frac{2}{\epsilon }\left|t_1-t_2\right|.$

当 $\frac{\epsilon }{2}>t_1>-\frac{\epsilon }{2}>t_2$ 时，有：

$\left|{{\phi }^{\prime }}_1\left(\epsilon ,t_1\right)-{{\phi }^{\prime }}_1\left(\epsilon ,t_2\right)\right|=\left|\frac{2t_1}{\epsilon }+1\right|<\left|\frac{2t_1}{\epsilon }-\frac{2t_2}{\epsilon }\right|=\frac{2}{\epsilon }\left|t_1-t_2\right|.$

当 $t_1>\frac{\epsilon }{2}>-\frac{\epsilon }{2}>t_2$ 时，有：

$\left|{{\phi }^{\prime }}_1\left(\epsilon ,t_1\right)-{{\phi }^{\prime }}_1\left(\epsilon ,t_2\right)\right|=2=\frac{2}{\epsilon }\epsilon \le \frac{2}{\epsilon }\left|t_1-t_2\right|.$

当 $t_1>t_2>\frac{\epsilon }{2}$ 或 $-\frac{\epsilon }{2}>t_1>t_2$ 时，有：

$\left|{{\phi }^{\prime }}_1\left(\epsilon ,t_1\right)-{{\phi }^{\prime }}_1\left(\epsilon ,t_2\right)\right|=0\le \frac{2}{\epsilon }\left|t_1-t_2\right|.$

令 $L_1=\frac{2}{\epsilon }$ ，同理可证存在常数 $L_2$ 使得 ${{\phi }^{\prime }}_2\left(t\right)$ 在紧集D上Lipschitz连续。

最终令 $L_m=\max \left\{L_1,L_2\right\}$ ，我们得到：

$\left|{{\phi }^{\prime }}_i\left(\epsilon ,t_1\right)-{{\phi }^{\prime }}_i\left(\epsilon ,t_2\right)\right|\le L_m\left|t_1-t_2\right|,\forall t_1,t_2\in D,i=1,2.$

引理4 函数 ${\varphi }_i\left(\epsilon ,x\right)$ 由(7)所定义，则 $\nabla {\varphi }_i\left(\epsilon ,x\right)$ 在紧集D上Lipschitz连续。

证明：计算得：

${\left[\nabla {\varphi }_i\left(\epsilon ,x\right)\right]}_j={\left({\displaystyle \underset{j=1}{\overset{n}{\sum }}{\phi }_i^p\left(\epsilon ,x_j\right)}\right)}^{\frac{1-p}{p}}{\phi }_i^{p-1}\left(\epsilon ,x_j\right){\phi }^{\prime }\left(\epsilon ,x_j\right).$

因 ${\phi }_i$ 连续可微，且 $\epsilon \ne 0,{\phi }_i\ne 0$ ，我们有 ${\left({\displaystyle \underset{j=1}{\overset{n}{\sum }}{\phi }_i^p\left(\epsilon ,x_j\right)}\right)}^{\frac{1-p}{p}}$ 和 ${\phi }_i^{p-1}$ 均连续可微。假设集合D有界，则D为紧集，由引理1知 ${\left({\displaystyle \underset{j=1}{\overset{n}{\sum }}{\phi }_i^p\left(\epsilon ,x_j\right)}\right)}^{\frac{1-p}{p}}$ 及 ${\phi }_i^{p-1}$ 在紧集D上Lipschitz连续。

同时由引理3可知 ${\phi }^{\prime }\left(\epsilon ,x_j\right)$ 在紧集D上Lipschitz连续，则由引理2可知：

${\left({\displaystyle \underset{j=1}{\overset{n}{\sum }}{\phi }_i^p\left(\epsilon ,x_j\right)}\right)}^{\frac{1-p}{p}}\cdot {\phi }_i^{p-1}\left(\epsilon ,x_j\right)\cdot {\phi }^{\prime }\left(\epsilon ,x_j\right)$ 在紧集D上Lipschitz连续，记Lipschitz常数为 $L_D$ ，那么有：

$\Vert \nabla {\varphi }_i\left(\epsilon ,x\right)-\nabla {\varphi }_i\left(\epsilon ,y\right)\Vert \le {\displaystyle \underset{j=1}{\overset{n}{\sum }}\Vert {\left[\nabla {\varphi }_i\left(\epsilon ,x\right)\right]}_j-{\left[\nabla {\varphi }_i\left(\epsilon ,y\right)\right]}_j\Vert }\le n{L}_D\Vert x-y\Vert .$

即 $\nabla {\varphi }_i\left(\epsilon ,x\right)$ 在紧集D上Lipschitz连续。

引理5 $\nabla {\Vert x\Vert }_2$ 在紧集D上Lipschitz连续。

证明：计算得 $\nabla {\Vert x\Vert }_2=\left[\frac{x_1}{{\Vert x\Vert }_2},\frac{x_2}{{\Vert x\Vert }_2},\cdots ,\frac{x_n}{{\Vert x\Vert }_2}\right]$ ，由引理1可知 $\frac{x_j}{\Vert x\Vert }$ 在水平集上光滑，则 $\frac{x_j}{\Vert x\Vert }$ 在紧集D上Lipschitz连续，记Lipschitz常数为 $L_c$ ，则：

$\Vert \nabla {\Vert x\Vert }_2-\nabla {\Vert y\Vert }_2\Vert \le n{L}_c\Vert x-y\Vert .$

引理6 目标函数梯度 $\nabla G_i\left(x\right)$ 由(9)所定义，则 $\nabla G_i\left(x\right)$ 在紧集D上Lipschitz连续。

证明：计算得 $\nabla G_i\left(x\right)={\lambda }_1\nabla {\phi }_i\left(\epsilon ,x\right)+{\lambda }_2\nabla {\Vert x\Vert }_{2,\mu }+A^{\text{T}}\left(Ax-b\right)$ ，则：

$\begin{array}{l}\Vert \nabla G_i(x)-\nabla G_i(y)\Vert \\ =\Vert {\lambda }_1\nabla {\varphi }_i\left(\epsilon ,x\right)+{\lambda }_2\nabla {\Vert x\Vert }_{2,\mu }+A^{\text{T}}\left(Ax-b\right)-{\lambda }_1\nabla {\varphi }_i\left(\epsilon ,y\right)-{\lambda }_2\nabla {\Vert y\Vert }_{2,\mu }-A^{\text{T}}\left(Ay-b\right)\Vert \\ \le {\lambda }_{1}n{L}_D\Vert x-y\Vert +{\lambda }_{2}n{L}_C\Vert x-y\Vert +{\Vert A\Vert }_2^2\Vert x-y\Vert \\ =\left({\lambda }_{1}n{L}_D+{\lambda }_{2}n{L}_C+{\Vert A\Vert }_2^2\right)\Vert x-y\Vert .\end{array}$

3. 基于非精确线搜索的三项共轭梯度法

求问题 $\underset{x\in R^n}{\text{min}}f\left(x\right)$ 的共轭梯度法的具体迭代过程如下：

$\begin{array}{l}{x}_{k+1}=x_k+{\alpha }_k{d}_k,\\ d_k=\{\begin{array}{l}-g_k,k=0,\\ -g_k+{\beta }_{k-1}{d}_{k-1},k>0.\end{array}\end{array}$

其中 $x_k$ 代表当前迭代点， $d_k$ 代表当前搜索方向， ${\alpha }_k$ 代表搜索步长， $g_k=\nabla G\left(x_k\right)$ ，不同的 ${\beta }_k$ 代表不同

的共轭梯度算法。Shouqiang Du和Miao Chen在文献 [9] 中提出了一种新型三项共轭梯度法。具体迭代过程如下：

$d_k=\{\begin{array}{l}-g_k,k=0,\\ -g_k+{\beta }_{k-1}{d}_{k-1}-{\theta }_{k-1}{y}_{k-1},k>0.\end{array}$

其中新加入项 $-{\theta }_{k-1}{y}_{k-1}$ 可以每步迭代确保目标函数值严格下降，使计算效率更高.本文将利用该共轭梯度法解决信号恢复问题。

算法1 (基于非精确线搜索的共轭梯度法)

步0给出初始参数 $\mu ,\epsilon ,\eta ,\delta ,{\lambda }_1,{\lambda }_2,\rho ,\sigma ,x_0,{\mu }_0,\gamma$ ，置 $k:=0$ 。

步1若满足终止准则 $\Vert \nabla G_i\left(x\right)\Vert <\epsilon$ ，停止计算，输出结果 $x_k\approx x^{*}$ ；否则，转步2。

步2计算搜索方向：

$d_k=\{\begin{array}{l}-g_k,k=0,\\ -g_k+{\beta }_{k-1}{d}_{k-1}-{\theta }_{k-1}{y}_{k-1},k>0.\end{array}$

其中，

$y_k=g_k-g_{k-1},{\beta }_k=\frac{g_k^{\text{T}}{y}_{k-1}}{-\eta g_{k-1}^{\text{T}}{d}_{k-1}+\mu \left|g_k^{\text{T}}{y}_{k-1}\right|},{\theta }_k=\frac{g_k^{\text{T}}{d}_{k-1}}{-\eta g_{k-1}^{\text{T}}{d}_{k-1}+\mu \left|g_k^{\text{T}}{y}_{k-1}\right|}.$

步3令 ${\alpha }_k=\text{max}\left\{{\rho }^m:m=0,1,2,\cdots \right\}$ ，同时满足：

$G\left(x_k+{\alpha }_k{d}_k\right)>G\left(x_k\right)-2\sigma \left(1-\gamma {\mu }_0\right){\alpha }_{k}G\left(x_k\right).$

步4令 $x_{k+1}=x_k+{\alpha }_k{d}_k$ ，计算 $g_{k+1}=\nabla G\left(x_{k+1}\right)$ 。

步5令 $k:=k+1$ ，转步1。

假设1令 $c>0$ 为常数，假设水平集 $L_c=\left\{x_k|G\left(x_k\right)\le c\right\}$ 是紧集。

定理1 若 $\left\{x_k\right\}$ 是由算法1产生的序列，则：

$\underset{k\to 0}{\text{lim}}\Vert \nabla G\left(x_k\right)\Vert =0.$

证明：由文献 [9] 中定理6，本文引理6及假设1可得。

4. 数值实验

本节实验在Intel Core i7-6500U 2.50GHz CPU，8G RAM，Windows10 64位操作系统，MATLAB R2016a环境下进行，所有数值实验结果为测试十次取平均值。

我们对两个不同的绝对值近似函数 ${\phi }_1$ 和 ${\phi }_2$ 分别在信号维数n取2048，4096，8192三种情况下，测试随机信号在无噪声和存在噪声干扰时的恢复效果.通过对比信号恢复时间t，相对误差e和迭代步数k来比较范数p和R对算法对信号恢复效果的影响。参数取值如下：A为 $m\times n$ 的随机高斯矩阵，x为n维随机初始信号， $x0=zeros\left(n,1\right)$ 为初始点， $gs=normnd\left(0,0.01,n/2,1\right)$ 是一个平均值是0，标准差是0.01的对观测向量b的噪声干扰，p取0.3，0.4，0.5，0.6，R取0，1，10，100 (当R = 0时代表2范数项为0，即目标函数为p范数模型)，其他参数取值如下：

$\mu =1e-5,\epsilon =1e-5,\eta =1,\delta =2,\lambda =1e-6\ast {\Vert A^{\text{T}}b\Vert }_{\infty },\rho =0.5,\sigma =0.002,\gamma =\mathrm{0.2.}$

1) 我们先对绝对值近似函数 ${\phi }_1$ 的信号恢复问题进行数值实验，结果如表1至表6所示：

Table 1. Signal dimension n = 2048, no noise interference

表1. 信号维数n = 2048，无噪声干扰

Table 2. Signal dimension n = 2048, Gauss noise interference

表2. 信号维数n = 2048，高斯噪声干扰

Table 3. Signal dimension n = 4096, no noise interference

表3. 信号维数n = 4096，无噪声干扰

Table 4. Signal dimension n = 4096, Gauss noise interference

表4. 信号维数n = 4096，高斯噪声干扰

Table 5. Signal dimension n = 8192, no noise interference

表5. 信号维数n = 8192，无噪声干扰

Table 6. Signal dimension n = 8192, Gauss noise interference

表6. 信号维数n = 8192，高斯噪声干扰

2) 我们再对绝对值近似函数 ${\phi }_2$ 的信号恢复问题进行数值实验，结果如表7至表12所示：

Table 7. Signal dimension n = 2048, no noise interference

表7. 信号维数n = 2048，无噪声干扰

Table 8. Signal dimension n = 2048, Gauss noise interference

表8. 信号维数n = 2048，高斯噪声干扰

Table 9. Signal dimension n = 4096, no noise interference

表9. 信号维数n = 4096，外界无噪声干扰

Table 10. Signal dimension n = 4096, Gauss noise interference

表10. 信号维数n = 4096，高斯噪声干扰

Table 11. Signal dimension n = 8192, no noise interference

表11. 信号维数n = 8192，无噪声干扰

Table 12. Signal dimension n = 8192, Gauss noise interference

表12. 信号维数n = 8192，高斯噪声干扰

5. 主要结论

通过在不同维度n = 2048，4096，8192下做信号恢复效果分析，我们主要得出以下结论：

1) 相对于p范数模型， $l_p+l_2$ 范数模型具有更好的恢复效果，二者在时间和迭代步数相近的情况下， $l_p+l_2$ 范数模型对初始信号的精度更高。

2) 做 ${\lambda }_{\text{2}}/{\lambda }_{\text{1}}$ 的值对信号恢复效果影响的横向对比， ${\lambda }_{\text{2}}/{\lambda }_{\text{1}}$ 的取值对信号恢复的时间和迭代步数影响并不明显；但是 ${\lambda }_{\text{2}}/{\lambda }_{\text{1}}=1$ 或 ${\lambda }_{\text{2}}/{\lambda }_{\text{1}}=10$ 时信号的恢复具有更高精度，这是由于当 ${\lambda }_{\text{2}}/{\lambda }_{\text{1}}$ 取值为1~10时2范

数项对p范数的调节使得函数模型的非凸性程度降低，因而提高信号恢复的精度。

3) 做p的值对信号恢复效果影响的纵向对比，显然范数p = 0.6时信号恢复的精度最高，p = 0.3时精度最低。

注：1) 文献 [10] 中提出的模型为

$\begin{array}{l}\underset{x\in R^n}{\min }\lambda {\Vert x\Vert }_1-\tau {\Vert x\Vert }_2,\\ \text{s}\text{.t}\text{.}Ax=b.\end{array}$

即利用 $l_1-l_2$ 范数加权从而产生稀疏阶，而本文考虑p范数比1范数更易得到稀疏解，从而利用 $l_p+l_2$ 范数加权进行信号恢复。

2) 文献 [10] 中的光滑化绝对值函数是文献 [8] 中 ${\phi }_3$ 。

3) 文献 [11] 中的模型为：

$\underset{x\in R^n}{\min }{\lambda }_1{\Vert x\Vert }_p^p+{\lambda }_2{\Vert x\Vert }_2^2+\frac{1}{2}{\Vert Ax-b\Vert }_2^2.$

而 ${\lambda }_1{\Vert x\Vert }_p^2+{\lambda }_2{\Vert x\Vert }_2^2$ 较 ${\lambda }_1{\Vert x\Vert }_p+{\lambda }_2{\Vert x\Vert }_2$ 不易产生稀疏解。取p = 0.3，R = 100对比图形如图5和图6所示：

Figure 5. ${\lambda }_1{\Vert x\Vert }_p^p+{\lambda }_2{\Vert x\Vert }_2^2$ norm image

图5. ${\lambda }_1{\Vert x\Vert }_p^p+{\lambda }_2{\Vert x\Vert }_2^2$ 范数图像

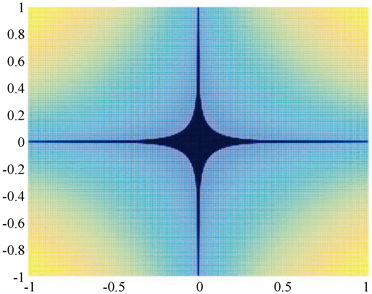
Figure 6. ${\lambda }_1{\Vert x\Vert }_p+{\lambda }_2{\Vert x\Vert }_2$ norm image

图6. ${\lambda }_1{\Vert x\Vert }_p+{\lambda }_2{\Vert x\Vert }_2$ 范数图像

基金项目

内蒙古自然科学基金(2018MS01016)。

NOTES

^*通讯作者。