基于移动轨迹数据的城市基站人流预测研究

Urban Base Station Traffic Forecasting Based on Mobile Trajectory

摘要: 城市通讯基站负载日益增长且不均衡，为优化基站资源调度分配，提高基站服务质量，提出了一种基于时空关联特征的GA-BP神经网络分钟级多步预测方法。本研究基于移动用户轨迹数据，建立基站间负载时空转移概率矩阵，提取影响基站负载的时空因素。针对BP神经网络存在易陷入局部极小值的问题，使用遗传算法对BP神经网络的初始权值和阈值进行优化，构建GA-BP神经网络模型进行分钟级负载预测模型。该模型基于某运营商脱敏后的移动用户轨迹数据进行训练与预测，结果显示，基于时空关联特征的GA-BP模型能有效对基站分钟级多步负载进行预测。

Abstract: Communication base station load is increasing and unbalanced. In order to optimize base station resource scheduling and improve base station service quality, we proposed a model of multi-step base station load prediction in minute-level with spatio-temporal correlation data based on BP neural network optimized by genetic algorithm. By using mobile user trajectory data, we estab-lished the spatio-temporal transition probability matrix between base stations and extracted the spatio-temporal features which affect the base station load. As BP neural network easily got into the local extremes, genetic algorithm was employed to optimize the initial weights and thresholds of BP network model. The algorithm proposed is verified by a mobile user trajectory dataset encrypted by the operator. The results showed that the optimized model with spatio-temporal correlation features can effectively predict the multi-step base station load in minute-level.

1. 引言

当下无线移动应用持续增长，通讯基站的负载压力不断增大且不均衡。对基站负载进行细粒度多步预测有助于对基站资源进行实时动态规划，优化资源配置，提高基站资源利用率并提升服务水平。

目前，国内外在进行负载预测的研究中，主要包括公交负载预测 [1] [2] 、城市交通流量预测 [3] [4] [5] 、基站服务负载预测 [6] [7] [8] [9] [10] 等，预测结果通常分为单步预测 [3] [5] 和多步预测 [11] [12] ，预测方法主要包括神经网络预测 [1] [2] [3] 、时间序列预测 [7] [13] 、马尔科夫模型 [8] [1] 、GBDT算法 [15] 等。在基站的负载预测中，王凯 [6] 等构建移动基站接入设备量和人群聚集量之间的数学模型，基于移动网络估算某一特定区域的人员密度，并通过回归分析证明通过移动网络估计人员密度是可行的。孙莹 [7] 等利用3G用户上网数据推演了群体分布动态聚散过程，并依此提出了基站人群时空预测模型与方法，相比于以往单一时间序列预测的方法，进一步提高了基站分时负载预测的精度。方志祥 [8] 等从群体角度出发，采用手机位置数据，考虑人群移动的时空差异，结合马尔可夫链的无后效性和贝叶斯定理，提出一种城市区域尺度上的基站服务用户数预测方法。该方法计算手机位置的时空转移概率，构建基站服务用户数预测模型，实现城市区域内的不同时间粒度上的基站负载预测。上述方法都对基站负载进行了不同时间粒度上的预测，但是没有考虑进行基站负载的分钟级多步预测。

本文提出的一种基于时空关联特征的GA-BP神经网络分钟级多步预测模型，能够快速对基站的负载进行更细时间粒度上的多步预测，从而灵活快速对基站资源进行优化。首先，分析目标基站负载变化的时间因素，提取目标基站的时间因子及周期因子。同时，通过建立基站间负载时空转移概率矩阵，提取目标基站的关联基站，作为目标基站的空间因子。最后，实现BP神经网络的基站负载预测。针对BP神经网络存在易陷入局部极小值的问题，使用遗传算法对BP神经网络的初始权值和阈值进行优化，最终实现高精度的基站负载分钟级多步预测。

2. 理论方法

2.1. 时空影响因素分析

移动用户通过连接基站获取网络，在用户移动的过程中，信号在基站之间的切换也代表着人群在基站间的流动，当前基站的负载可看做上一时刻人群数的延续和其他基站人群的转移。移动用户的上学、上班、购物等行为都有着一定的规律性，基站的负载也会产生周期性的变化。因此，在考虑基站负载变化的时空影响因素中，我们从以下三点来考虑：1) 当前时间的基站负载可以看做前一时段人群数的延续。2) 当前时间的基站负载变化规律可看做是周期循环的结果。3) 当前基站的负载可以看做是其他基站人群数共同影响的结果。

多步预测指的是假设样本数量为N，在无法得到新的时间序列采样或者只利用该N个样本，在单步预测第N+1个值之外，也可以预测第 $N+2,N+3,\cdots ,N+T\left(T>0\right)$ 个值，即通过己知的样本集可以外推进行T步预测。在基站负载的分钟级多步预测中，我们以分钟作为时间粒度，对基站负载进行未来N + T个时段的预测，从而可以为基站资源的调控提供决策数据，进行资源优化。

本文根据基站负载的时空关联性，参考丁闪闪 [3] 等在交通参数预测中的定义，选定3类要素因子来标定影响因素，分别命名为时间因子(相邻时段的影响)、周期因子(周期性重复的影响)和空间因子(基站间转移的影响)。其中：

1) $I:I=\left\{i_1,i_2,\cdots ,i_n\right\}$ 表示某区域基站集合。

2) $N_{I_j}^{t+T}:N_{I_j}^{t+T}$ 表示第I_j个基站的T步负载预测值。 $T=1，2，3，\cdots$ 。

3) k:表示与时段t具有时间关联性的前第k个时段，即第k个时间因子， $k=i-1,i-2,i-3，\cdots ,i-n$ 。

4) l表示与当前日具有相似模式的前第l个周期，其中 $l=i-1,i-2,i-3，\cdots ,i-m$ 。

5) s:表示与该基站具有空间关联性的第s个基站，其中 $s=0，1，2，\cdots ,o$ 。

在确定目标基站的空间因子时，本文参考方志祥 [8] 等的研究，从群体角度出发，建立基站间转移概率矩阵，构造基站间的关联关系。在选定某基站的空间因子时，根据基站间转移概率进行排序，概率越大说明该基站对目标基站的负载影响越大，选定前s个基站作为空间关联因素。

在基站负载影响因素的选取中，本文初步选定影响该基站负载的前k个时刻的时间因子、与当前日具有相似模式的前l个周期的周期因子和与该基站具有空间关联性的前s个空间因子。当我们用时空因素(k,l,s)来表示基站T-步预测模型时，可得出

$N_{I_j}^{t+T}=f\left(N_{I_j}^{t+k},N_{I_j}^{t_l+k},N_{I_j}^{t_l+T},N_{I_S}^{t+k}\right)$ (1)

其中 $T=1，2，\cdots ,m$ ; $k=1，2，\cdots ,T$ ; $l=1，2，\cdots ,m$ ; $s=1，2，\cdots ,n$ 。

2.2. 基于遗传算法优化的BP神经网络模型

2.2.1. BP神经网络

BP神经网络是一种有监督学习的多层前馈神经网络，也是目前使用最广泛的神经网络模型。当输入节点数为n，输出节点数为m时，BP神经网络可以映射为n个自变量到m个因变量的非线性函数。BP神经网络模型训练时，按照误差反向传播机制不断调整网络权值和阈值，不断逼近期望输出值，因此，BP神经网络可以拟合任意连续函数 [16] [17] [18] 。

传统BP神经网络按照梯度下降的方式修正网络权值和阈值，有容易陷入局部极值，不能搜索到全局最优解的缺陷。

2.2.2. 遗传算法优化的BP神经网络

BP神经网络在训练时需要对网络各层的连接权值和阈值进行随机赋值，这种随机初始化往往会影响BP神经网络的收敛速度和最终结果。针对这个问题，本文依靠遗传算法的全局寻优能力，将BP神经网络的训练误差作为遗传算法的评价标准来寻找BP神经网络的初始权值和阈值，然后将该初始权值和阈值赋予BP神经网络，然后对BP神经网络预测模型进行训练，从而得到最优的输入–输出映射模式，如图1所示。

Figure 1. BP neural network optimized by genetic algorithm

图1. GA-BP多步预测模型

3. 实例分析

3.1. 数据准备

本研究采用的实验数据为某城市2017年6月26日~8月29日的移动用户轨迹数据，脱敏后的轨迹数据以手机基站的经纬度坐标记录用户的位置信息，以连接时间记录用户的时间信息，如表1所示。

Table 1. Mobile user trajectory data instance

表1. 移动用户轨迹数据样例

在研究中，我们需要对移动用户轨迹数据进行清洗，去除重复、无效、缺失日期的数据。然后以10分钟作为间隔时段，统计基站的负载数据及基站之间的转移，作为实验的样本数据，如表2所示。

Table 2. Base station load statistical results

表2. 每基站负载统计表

3.2. 影响因素选取

3.2.1. 时间因子

在基站的分钟级多步预测中，本文首先基于人群白天活动夜晚休息的规律，选择9点~21点作为待预测时段。在预测时段的时间影响因子选取时，考虑下一时刻的负载数据可以认为是当前时刻负载的聚集及影响。因此选定当前时刻的6个负载数据作为时间因子。例如预测6月26日的9:10, 9:20, 9:30, 9:40, 9:50, 9:60六个时段的负载数据，选定6月26日的8:10, 8:20, 8:30, 8:40, 8:50, 8:60作为时间因子输入到模型中，结果如图2所示。

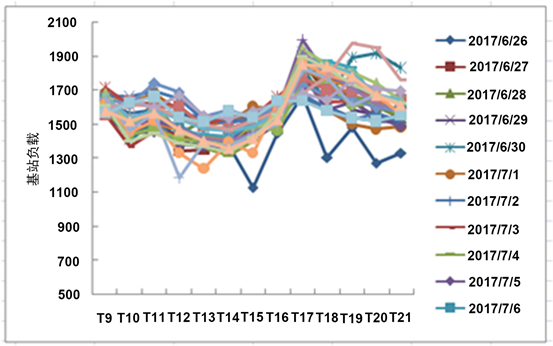
Figure 2. Base station load on 9:00~21:00

图2. 部分日期9:00~21:00基站负载变化

3.2.2. 周期因子

在对数据进行周期性统计的过程中，可以发现基站的人群运动模式呈现星期稳定性。在不同时间段的基站负载数据中，呈现着相同的周期模式。因此，可以采用周期因子作为预测模型的影响因素。例如预测7月3日的9:10, 9:20, 9:30, 9:40, 9:50, 9:60六个时段的负载数据，选定7月3日的8:10, 8:20, 8:30, 8:40, 8:50, 8:60以及9:10, 9:20, 9:30, 9:40, 9:50, 9:60作为周期因子输入到模型中，结果如图3和图4所示。

Figure 3. Base station load on monday

图3. 某基站周一负载变化图

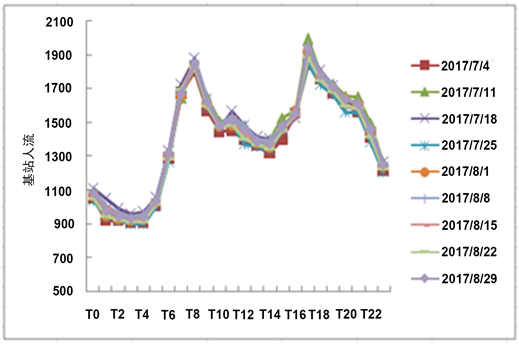
Figure 4. Base station load on sunday

图4. 某基站周日负载变化图

3.2.3. 空间因子

在空间因子的选取过程中，首先统计不同时段各基站的负载数据以及基站之间人群相互转移的数据，计算手机用户群体在基站间的转移概率矩阵,矩阵部分数据如下图5所示。

同时基于选定的预测目标基站A，在转移概率矩阵中可发现有向基站A转移负载的概率矩阵如下表3所示，从表中发现有21个基站的人群会向A基站转移。在该矩阵中，概率最大的前五个基站转移人流占据总人流的80.8%，因此选择向该基站转移人群数的概率最大的前5个基站B, R, I, T, U作为影响基站下一时刻负载的空间因子。例如预测6月26日A基站的9:10, 9:20, 9:30, 9:40, 9:50, 9:60六个时段的负载数据，选定6月26日B, R, I, T, U五个基站的8:10, 8:20, 8:30, 8:40, 8:50, 8:60作为空间因子输入到模型中，如表3所示。

Figure 5. Base station load transition probability matrix

图5. 某区域基站转移概率矩阵

Table 3. A base station load transition probability matrix

表3. A基站负载转移概率矩阵

3.3. 模型构建

在上文的时间因子、周期因子和空间因子确定之后，因为需要提前一周数据作为周期因子并且预测时段为9点~21点，可选择的样本数据共为7月3日~8月29日共60天，每天预测时段为12个小时，共有样本数据为720组。随机选择N组样本数据作为训练样本，720-N组样本数据作为测试样本。

在设计BP神经网络模型的输入和输出时，假设选择输出为A基站的7月3日的9:10, 9:20, 9:30, 9:40, 9:50, 9:60，那么对应的输入则为A基站7月3日的8点6个数据、6月26日的8点和9点12个数据，5个关联基站的7月3日的8点的(6 × 5) 30个数据，总共48个数据作为输入数据。为了提高网络的训练速率，便于网络的计算，本文使用premnmx函数对原始数据样本进行归一化处理，使处理后的数据均匀地分布在[−1,1]的范围内。预测结果采用平均相对误差MAPE，平均绝对误差MAE，均方误差MSE，均方根误差RMSE等指标进行评价。各指标的计算公式如下：

$MAPE=\frac{1}{N}{{\displaystyle \sum }}^{\text{}}\left|\frac{Y_{pre}^t-Y_{test}^t}{Y_{test}^t}\right|$ (2)

$MAE=\frac{1}{N}{{\displaystyle \sum }}^{\text{}}\left|Y_{pre}^t-Y_{test}^t\right|$ (3)

$MSE=\frac{1}{N}{{\displaystyle \sum }}^{\text{}}{\left|Y_{pre}^t-Y_{test}^t\right|}^2$ (4)

$RMSE=\sqrt{\frac{1}{N}{{\displaystyle \sum }}^{\text{}}{\left|Y_{pre}^t-Y_{test}^t\right|}^2}$ (5)

本文采用单隐层的BP神经网络进行实现，输入层节点数为48个，隐含层节点数采用试算法得到为14个，输出层节点数为6个，设置的BP神经网络结构为48-14-6，共有48 × 14 + 6个权值，14 + 6个阈值。其节点传递函数采用对数型S函数和线性函数，训练函数采用 L-M 优化算法。BP神经网络训练次数取100，学习率取0.1。

遗传算法用来优化BP神经网络的初始权值和阈值，因此遗传算法个体编码长度为698。遗传算法初始种群规模取20，进化代数取30次，交叉概率取0.3，变异概率取 0.01。

3.4. 结果分析

神经网络的预测准确性和训练数据的多少有较大的关系，尤其对于一个多输入和多输出的网络，所以本文首先基于不同的训练样本数据进行模型训练，对多步预测结果的误差进行均值计算。最后结果显示当样本数据为660，测试数据为60时，多次试验结果的评价较好，因此选用当前样本数据集合进行模型预测(表4)。

Table 4. Different number of training data prediction error

表4. 不同数目训练样本预测误差

使用处理好的数据分别对BP神经网络和遗传算法优化的神经网络进行测试，多步预测结果中的6个被预测时刻的预测结果如图6、图7、图8、图9、图10、图11所示。

从图6~图11中可以看出，使用遗传算法优化过的模型得出的预测结果与期望输出的结果值更加接近，误差值更小。在多步预测的结果值中，越接近当前时刻，预测的准确度更高，T + 1时刻的预测值相比T + 2之后时段的预测值准确度更高，说明随着时间的推移，基站负载的转移具有了变化，模型还不能通过时段之间的变化更好的把握这种变化规律，多步预测的结果随着预测时间段的加长，准确率会逐渐降低。

预测结果的评价指标如表5所示。通过实验评价指标可以看出，优化后的预测模型在平均相对误差MAPE，平均绝对误差MAE，均方误差MSE，均方根误差RMSE四个指标上对于基本的BP模型都有所降低，说明遗传算法优化后的BP神经网络能够提高预测的精度。

4. 结论

针对基站负载分钟级多步预测问题，本文基于实际的手机轨迹数据，提取目标基站的时间及周期因子。通过建立基站间负载转移概率矩阵，提取目标基站的关联基站作为空间因子。以BP神经网络进行

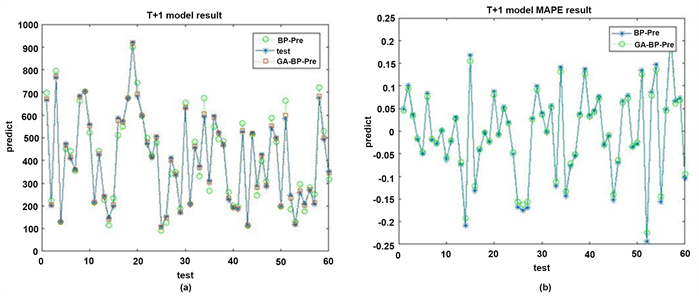
Figure 6. (a) T + 1 two model results; (b) T + 1 two model error

图6. (a) T + 1时刻两种模型结果；(b) T + 1时刻两种模型误差

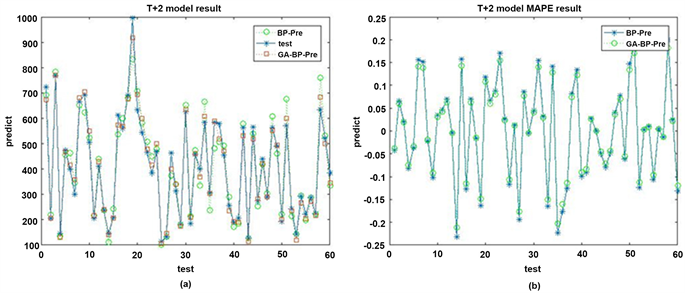
Figure 7. (a) T + 2 two model results; (b) T + 2 two model error

图7. (a) T + 2时刻两种模型结果；(b) T + 2时刻两种模型误差

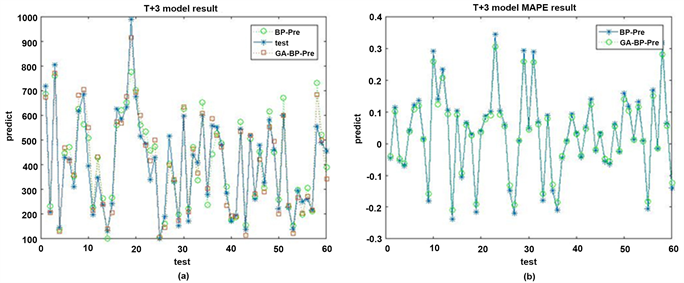
Figure 8. (a) T + 3 two model results; (b) T + 3 two model error

图8. (a) T + 3时刻两种模型结果；(b) T + 3时刻两种模型误差

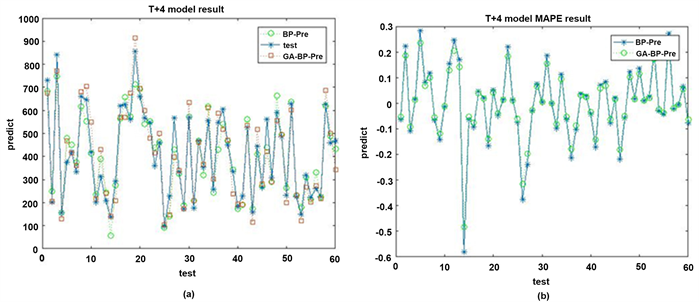
Figure 9. (a) T + 4 two model results; (b) T + 4 two model error

图9. (a) T + 4时刻两种模型结果；(b) T + 4时刻两种模型误差

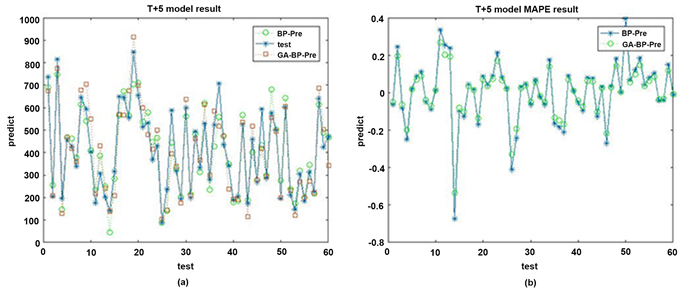
Figure 10. (a) T + 5 two model results; (b) T + 5 two model error

图10. (a) T + 5时刻两种模型结果；(b) T + 5时刻两种模型误差

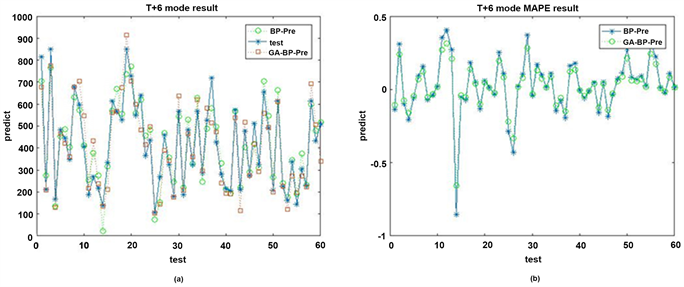
Figure 11. (a) T + 6 two model results; (b) T + 6 two model error

图11. (a) T + 6时刻两种模型结果；(b) T + 6时刻两种模型误差

Table 5. Multi-step prediction results error statistics

表5. 多步预测结果误差统计表表

基站负载预测，针对BP神经网络存在易陷入局部极小值的问题，使用遗传算法对BP神经网络的初始权值和阈值进行优化。结果显示，将基站负载的时空影响因素作为输入并且使用基本的BP模型进行预测，能够实现分钟级的基站负载多步预测，为基站的资源动态优化提供数据参考。针对BP神经网络预测精度低的问题，遗传算法优化后的BP网络模型能够提高多步预测结果的精度。此外，在多步预测中，随着预测时间间隔的增加，BP神经网络模型的预测精度逐渐下降。但是经过遗传算法优化后的BP神经网络模型，对于预测时间间隔较远的时刻，预测精度也有了明显的提高。