加热梯度泡沫材料圆板的过屈曲

Post-Buckling of Heated Gradient Foam Material Circular Plates

摘要: 研究了梯度泡沫材料圆板的热过屈曲行为。基于von’Kaman经典板理论，假设泡沫梯度的密度沿厚度方向按照幂函数连续变化，建立了加热梯度泡圆板过屈曲控制微分方程。采用打靶法求解了加热泡沫材料圆板的过屈曲数值解，给出了圆板的热过屈曲平衡路径和平衡构形。数值结果表明：材料的梯度指数和边界条件对圆板过屈曲行为都有重要影响。

Abstract: The thermal post buckling behavior of graded foamed circular plates was studied. Based on the von’Kaman classical plate theory, assuming that the density of the foam gradient changes contin-uously along the thickness direction according to the power function, the governing equation for the buckling of a heated gradient foam plate was established. The post-buckling numerical solution of a heated foamed circular plate was solved by shooting method, and the thermal post-buckling equilibrium path and equilibrium configuration of the circular plate were given. The numerical results show that the gradient index and boundary conditions of materials have important effects on the post-buckling behavior of circular plates.

1. 引言

金属泡沫或金属多孔材料是上世纪80年代后期国际上迅速发展起来的一种兼有结构材料和功能材料的特点的新型工程材料。金属泡沫由于其比重小、隔热性能好，被广泛应用于承受载荷与冲击的隔热材料而应用在航空和航天领域 [1] 。虽然早在上世纪40年代人们就成功地生产了泡沫铝，但对其力学行为却少有研究。究其原因，一方面是由于金属泡沫材料的制备工艺尚不成熟，难以得到性能稳定的材料；另一方面是缺少需求，人们还没有注意到它的潜在应用价值。因此，当时人们对泡沫材料研究的重点主要集中在聚合物发泡材料上，直到1959年描述泡沫材料力学性质的理论才由Gent和Thomas提出，从此奠定了泡沫力学研究的基础 [2] [3] [4] ，在此之后，人们对泡沫塑料的力学行为进行了广泛、深入和系统的实验研究和理论研究 [5] 。最近几年，有关金属泡沫材料的研究文献大量涌现，特别是金属泡沫材料力学行为的研究更是令人瞩目，成为泡沫力学研究的热点问题 [6] [7] [8] 。关永军等 [9] 主要从航空材料领域对材料基因组技术的角度，阐述了材料基因组技术的具体内涵，指出需要提供大量的热物性参数与本构模型用于材料的计算机模拟。提关于金属泡沫材料力学行为的研究早期的工作很少。董海凤等 [10] 详细阐述了泡沫金属材料孔结构力学行为的多方面研究成果，指出母体结构和孔隙率对泡沫材料受压和弯曲等方面的力学响应作了介绍，指出相对密度对泡沫金属材料的力学性能有重要影响。文献 [11] 针对厚度方向变密度的闭孔铝泡沫材料，建立了考虑密度变化影响的泡沫材料力学本构模型。闫长海 [12] 等建立了孔金属泡沫的一维传热模型，为开孔金属泡沫的热设计提供依据。

由以上文献调研发现，关于泡沫梯度材料的分析中，多数研究侧重于具体泡沫材料的制备和模拟以及宏观力学响应的分析方面，而对泡沫材料具体数值分析方面的研究十分有限，尤其缺乏加热泡沫材料的具体理论研究。本工作基于经典板理论，研究加热梯度泡沫材料金属圆板的稳定性问题。建立以横向和径向位移为基本未知量的加热梯度泡沫材料圆板过屈曲控制微分方程，采用打靶法 [13] 进行数值求解，分析材料梯度指数以及边界条件对泡沫圆板过屈曲行为的影响。

2. 基本方程

考虑图1所示一个由梯度泡沫材料制成的薄圆板，半径为a，厚度为h。设板自无约束状态起的均匀升温为T，考虑轴对称变形，中面过屈曲径向和横向位移分别为 $u\left(r\right)$ 和 $w\left(r\right)$ 。

2.1. FGMF的物性参数

根据Type1模型 [14] ，即板上下表面相对密度相同的对称泡沫材料板，其密度分布模式为

$\rho \left(z\right)={\rho }_0\left[n{s}^2-\frac{n}{12}+\frac{1}{2}\right]$ ， $n\in \left[-3,3\right]$ (1)

其中， $\rho \left(z\right)$ 为梯度泡沫材料密度(一般是材料内部各点位置的函数)； ${\rho }_0$ 为孔壁材料密度；n为材料梯度指数， $s=z/h$ 为坐标。Type1型泡沫材料密度随位置的变化如图2所示。

Figure 1. Coordinate system and geometric of gradient foam circular plates

图1. 梯度泡沫圆板坐标系与几何尺寸

Figure 2. Variations of the density along thickness of the FGMF plate for different values of n

图2. 泡沫梯度材料板密度在不同梯度下沿厚度的变化

梯度泡沫材料的物性参数P，这里泛指弹性模量 $E\left(z\right)$ 和热膨胀系数 $\alpha \left(z\right)$ ，一般是材料内部各点位置的函数，可描述为

$P\left(z\right)=P_0\lambda {\left(\frac{\rho \left(z\right)}{{\rho }_0}\right)}^m$ (2)

工程中一般取 $\lambda =1,m=2$ ，因此Type1模型下的弹性模量和热膨胀系数分别为

$E\left(z\right)=E_0{\left[n{\left(z/h\right)}^2-n/12+1/2\right]}^2$ (3)

$\alpha \left(z\right)={\alpha }_0{\left[n{\left(z/h\right)}^2-n/12+1/2\right]}^2$ (4)

其中， $E_0$ 和 ${\alpha }_0$ 分别为孔壁材料的弹性模量和热膨胀系数。

2.2. 控制微分方程

基于von Kármán 经典板理论，加热薄圆板的平衡方程如下

$N_r-N_{\theta }+r\frac{d{N}_r}{dr}=0$ (5)

$\frac{d^2{M}_r}{d{r}^2}+\frac{2}{r}\frac{d{M}_r}{dr}-\frac{1}{r}\frac{d{M}_{\theta }}{dr}+\frac{1}{r}\frac{d}{dr}r{N}_r\frac{\text{d}w}{\text{d}r}=0$ (6)

这里w为载荷产生的板中面横向挠度，r为径向坐标。

薄膜力 $N_r,N_{\theta }$ 和弯矩 $M_r,M_{\theta }$ 定义为

$\left(N_r,N_{\theta }\right)={\displaystyle {\int }_{-h/2}^{h/2}\left({\sigma }_r,{\sigma }_{\theta }\right)\text{d}z}$ (7)

$\left(M_r,M_{\theta }\right)={\displaystyle {\int }_{-h/2}^{h/2}\left({\sigma }_r,{\sigma }_{\theta }\right)z\text{d}z}$ (8)

由微分几何知识可得下列变形几何方程：

${\epsilon }_r^0=\frac{du}{dr}+\frac{1}{2}{\left(\frac{dw}{dr}\right)}^2$ ， ${\epsilon }_{\theta }^0=\frac{u}{r}$ (9)

${\kappa }_r=-\frac{d^{2}w}{d{r}^2}$ ， ${\kappa }_{\theta }=-\frac{1}{r}\frac{dw}{dr}$ (10)

线弹性材料板，其物理关系为

$\left(\begin{array}{c}{\sigma }_r\\ {\sigma }_{\theta }\end{array}\right)=\frac{E\left(z\right)}{1-{\nu }^2}\left[\begin{array}{cc}1& \nu \\ \nu & 1\end{array}\right]\left(\begin{array}{c}{\epsilon }_r^0\\ {\epsilon }_{\theta }^0\end{array}\right)+\frac{E\left(z\right)z}{1-{\nu }^2}\left[\begin{array}{cc}1& \nu \\ \nu & 1\end{array}\right]\left(\begin{array}{c}{\kappa }_r\\ {\kappa }_{\theta }\end{array}\right)$ (11)

这里， ${\sigma }_r$ 和 ${\sigma }_{\theta }$ 分别为r和 $\theta$ 方向的应力； ${\epsilon }_r^0$ 和 ${\epsilon }_{\theta }^0$ 为中曲面上的应变； ${\kappa }_r$ 和 ${\kappa }_{\theta }$ 为中面的曲率改变； $\nu$ 为泊松比。

将方程(6)~(7)代入(4)~(5)，可得下列关系

$\left(\begin{array}{c}{N}_r\\ N_{\theta }\end{array}\right)=A\left[\begin{array}{cc}1& \nu \\ \nu & 1\end{array}\right]\left(\begin{array}{c}{\epsilon }_r^0\\ {\epsilon }_{\theta }^0\end{array}\right)+B\left[\begin{array}{cc}1& \nu \\ \nu & 1\end{array}\right]\left(\begin{array}{c}{\kappa }_r\\ {\kappa }_{\theta }\end{array}\right)+\left(\begin{array}{c}{N}_T\\ N_T\end{array}\right)$ (12)

$\left(\begin{array}{c}{M}_r\\ M_{\theta }\end{array}\right)=B\left[\begin{array}{cc}1& \nu \\ \nu & 1\end{array}\right]\left(\begin{array}{c}{\epsilon }_r^0\\ {\epsilon }_{\theta }^0\end{array}\right)+D\left[\begin{array}{cc}1& \nu \\ \nu & 1\end{array}\right]\left(\begin{array}{c}{\kappa }_r\\ {\kappa }_{\theta }\end{array}\right)+\left(\begin{array}{c}{M}_T\\ M_T\end{array}\right)$ (13)

其中刚度系数 $A,B,D$ 可表示为

$\left(A,B,D\right)={\displaystyle {\int }_{-h/2}^{h/2}\frac{E\left(z\right)}{1-{\nu }^2}\left(1,z,z^2\right)\text{d}z}$ (14)

热薄膜力和热弯矩为

$\left(N_T,M_T\right)={\displaystyle {\int }_{-h/2}^{h/2}\frac{E\left(z\right)\alpha \left(z\right)T}{1-\nu }\left(1,z\right)\text{d}z}$ (15)

积分上式可得

$\left(A,B,D\right)=\frac{E_0}{1-{\nu }^2}\left(h{\varphi }_1,h^2{\varphi }_2,h^3{\varphi }_3\right)$ (16)

$\left(N_T,M_T\right)=\frac{E_0{\alpha }_{0}T}{1-\nu }\left(h{\varphi }_4+h^2{\varphi }_5\right)$ (17)

将式(9)~(10)以及式(12)~(13)代入方程(5)和(6)，可获得位移形式的无量纲基本控制方程如下：

$\frac{d^{2}U}{d{X}^2}+\frac{dU}{dX}-\frac{U}{X^2}+\frac{dW}{dX}\frac{d^{2}W}{d{X}^2}+\frac{1-\nu }{2X}{\left(\frac{dW}{dX}\right)}^2=\frac{{\varphi }_2}{{\varphi }_1}\left(\frac{d^{3}W}{d{X}^3}+\frac{d^{2}W}{d{X}^2}-\frac{1}{X^2}\frac{dW}{dX}\right)$ (18)

$\begin{array}{l}\frac{d^{4}W}{d{X}^4}+\frac{2}{X}\frac{d^{3}W}{d{X}^3}-\frac{1}{X^2}\frac{d^{2}W}{d{X}^2}+\frac{1}{X^3}\frac{dW}{dX}\\ =\frac{{\varphi }_1^2}{{\varphi }_1{\varphi }_3-{\varphi }_2^2}\left\{\left[\frac{\nu }{X}\frac{dU}{dX}+\frac{\nu }{2X}{\left(\frac{dW}{dX}\right)}^2+\frac{U}{X^2}\right]\frac{dW}{dX}+\left[\frac{dU}{dX}+\frac{1}{2}{\left(\frac{dW}{dX}\right)}^2+\frac{\nu }{X}U\right]\frac{d^{2}W}{d{X}^2}\right\}\\ -\frac{{\varphi }_1{\varphi }_2}{{\varphi }_1{\varphi }_3-{\varphi }_2^2}\left[{\left(\frac{d^{2}W}{d{X}^2}\right)}^2+\frac{1}{X^2}{\left(\frac{dW}{dX}\right)}^2+\frac{2\nu }{X}\frac{dW}{dX}\frac{d^{2}W}{d{X}^2}\right]-\frac{{\varphi }_1{\varphi }_4}{12\left({\varphi }_1{\varphi }_3-{\varphi }_2^2\right)}\left(\frac{1}{X}\frac{dW}{dX}+\frac{d^{2}W}{d{X}^2}\right)\tau \end{array}$ (19)

上述无量纲归一化变换如下：

$X=\frac{r}{a}$ ， $W=\frac{w}{h}$ ， $U=\frac{uR}{h^2}$ ， $\delta =\frac{a}{h}$ ， $\tau =12\left(1+\nu \right){\alpha }_{0}T{\delta }^2$ (20)

2.3. 量纲归一化边界条件

周边固支

$X=0$ 处， $U=0$ ， $\frac{dW}{dX}=0$ ， $\underset{X\to 0}{\lim }\left(\frac{d^{3}W}{d{X}^3}+\frac{1}{X}\frac{d^{2}W}{d{X}^2}\right)=0$ (21a)

在 $X=1$ 处， $W=0$ ， $U=0$ ， $\frac{dW}{dX}=0$ (21b)

周边不可移简支

$X=0$ 处 $U=0$ ， $\frac{dW}{dX}=0$ ， $\underset{X\to 0}{\lim }\left(\frac{d^{3}W}{d{X}^3}+\frac{1}{X}\frac{d^{2}W}{d{X}^2}\right)=0$ (22a)

$X=1$ 处 $W=0$ ， $U=0$ ， $\frac{dW}{dX}+\frac{1}{X}\frac{d^{2}W}{d{X}^2}=0$ (22b)

3. 数值结果与讨论

考虑梯度泡沫铝材圆板，常温20℃下的弹性模量 $E_0=69\text{GPa}$ ，热膨胀系数 ${\alpha }_{\text{0}}=\text{23}\times {\text{10}}^{-6}/\text{K}$ ，泊松比 $\nu =0.3$ 。由于非线性和耦合效应，很难求得常微分方程两点边值问题(18)~(22)的解析解。这里采用打靶法寻求数值解。为此，将方程(18)~(19)以及边界条件写成下式：

$\frac{\text{d}Y}{\text{d}\xi }=H\left(\xi ,Y\right),⤢⤢⤢\left(0<\xi <1\right)$ (23)

$B_{0}Y\left(0\right)=b_0$ , $B_{1}Y\left(1\right)=b_1$ (24)

其中

$Y={\left\{\begin{array}{ccccccc}{y}_1& y_2& y_3& y_4& y_5& y_6& y_7\end{array}\right\}}^{\text{T}}={\left\{\begin{array}{ccccccc}W& \frac{dW}{dX}& \frac{d^{2}W}{d{X}^2}& \frac{d^{3}W}{d{X}^3}& U& \frac{dU}{dX}& \lambda \end{array}\right\}}^{\text{T}}$

$\frac{dY}{dX}=H=\left(y_2,y_3,y_4,R_1,y_6,R_2,0\right)$

$R_1=-\left[\frac{y_6}{X}-\frac{y_5}{X^2}+y_2{y}_3+\frac{1-\nu }{2X}\right]+\frac{{\varphi }_2}{{\varphi }_3}\left[y_4+\frac{y_3}{X}-\frac{y_2}{X^2}\right]+y_7\frac{{\varphi }_3}{{\varphi }_1}$

$\begin{array}{c}{R}_2=-\left[\frac{2y_4}{X}-\frac{y_3}{X^2}+\frac{y_2}{X^3}\right]+\frac{{\varphi }_1^2}{{\varphi }_1{\varphi }_3-{\varphi }_2^2}\left[\frac{\nu }{X}{y}_2{y}_3+\frac{\nu }{2X}{y}_2^2+\frac{1}{X^2}{y}_2{y}_5+y_3{y}_6+\frac{1}{2}{y}_2^2{y}_3+\frac{\nu }{X}{y}_3{y}_5\right]\\ -\frac{{\varphi }_1{\varphi }_2}{{\varphi }_1{\varphi }_3-{\varphi }_2^2}\left[y_3^2+\frac{y_2^2}{X^2}+y_6+\frac{2\nu }{X}{y}_2{y}_3\right]+\frac{{\varphi }_2{\varphi }_3}{{\varphi }_1{\varphi }_3-{\varphi }_2^2}\frac{y_7}{X}\end{array}$

给定热载荷 $\lambda =\tau$ ，矩阵 $B_0$ 、 $B_1$ ，向量 $b_0$ 、 $b_1$ 的具体表达如下

$B_0=\left[\begin{array}{ccccccc}1& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0\\ 0& 0& -1/\Delta X& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0\end{array}\right]$ ， $b_0=\left\{\begin{array}{l}\xi \\ 0\\ 0\\ 0\end{array}\right\}$ ， (25)

周边固支

$B_1=\left[\begin{array}{ccccccc}1& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0\end{array}\right]$ ， $b_1=\left\{\begin{array}{l}0\\ 0\\ 0\end{array}\right\}$ (26)

周边简支

$B_1=\left[\begin{array}{ccccccc}1& 0& 0& 0& 0& 0& 0\\ 0& 1& 1/X& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0\end{array}\right]$ ， $b_1=\left\{\begin{array}{l}0\\ 0\\ 0\end{array}\right\}$ (27)

其中引入微小量 $\Delta X$ 是为了避免数值计算时在 $X=0$ 处引起奇异性。式中 $\xi =w\left(0\right)$ 。

下面考虑一个与边值问题相对应的初值问题：

$\frac{\text{dZ}}{\text{d}\xi }=H\left(\xi ,Y\right)$ (28a)

$\text{Z}\left(0\right)={\left\{0,d_1,0,\beta ,d_2,0,d_3\right\}}^{\text{T}}=I\left(\beta ,D\right)$ (28b)

其中， $D={\left\{d_1,d_2,d_3\right\}}^{\text{T}}$ 是与缺失的初始值相关的未知向量。这样，初值问题(13)可以表示为下面的式子，

$\text{Z}\left(\xi ,\beta ,D\right)=\text{Z}\left(0\right)+{\displaystyle {\int }_0^{\xi }H\left(\lambda ,\text{Z}\right)\text{d}}\lambda$ (29)

将板的中心挠度 $W\left(0\right)$ 作为过屈曲问题的控制参数，对于给定的W，我们寻找 $D$ 的各分量，使得方程(29)的解也满足边界条件(24)。这个过程就叫做打靶法。

图3和图4分别给出了热载荷作用下简支圆板和固支圆板中心挠度即最大挠度随热载荷 $\tau$ 之间的变化曲线。图中不难看出，不同梯度指数下，两种边界条件下，板都发生典型的分叉失稳。由分叉理论知道，曲线和横坐标的交点即为临界载荷，图中还不难看出，过屈曲后随着载荷的增大，不同梯度下板中心挠度也增大。

表1为泡沫材料在不同梯度下的临界温度 $T_{cr}$ 。可以看出，两种边界条件下，梯度指数从−3到1时临界温度增加，之后又开始减小。和预想的一样，同样梯度指数下，固支板的临界温度高于简支板的。

Table 1. Critical temperature of foam circular plates under different n

表1. 不同n下泡沫圆板的临界温度

Figure 3. Curves of thermal load vs. center deflection of the simply supported plate

图3. 简支圆板中心挠度–热载荷关系曲线

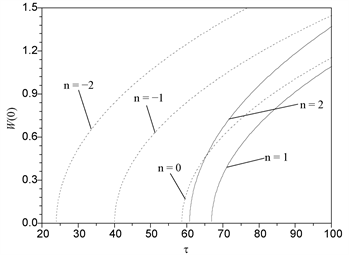
Figure 4. Curves of thermal load vs. center deflection of the clamped plate

图4. 固支圆板中心挠度–热载荷关系曲线

图5比较了两种边界下的过屈曲平衡路径。显然，在相同的梯度指数下，固支板具有更大的屈曲载荷，说明固支边界下的板具有更强的稳定性。

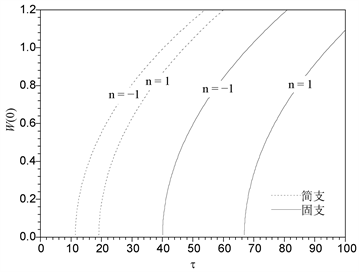
Figure 5. Comparison of post-buckling equilibrium path curves

图5. 过屈曲平衡路径比较曲线

图6和图7分别给出了不同梯度指数n下泡沫材料圆板的构形图，热载荷取固支 $\tau =70$ ，简支 $\tau =25$ 。 图中可以看出，梯度指数n对过屈曲平衡路径有显著的影响，意味着n的不同取值对梯度泡沫板刚度有很大影响。另外，从构形图看出，在边界处，板的变形也受到约束的影响，边界条件对泡沫材料板的过屈曲构形也有很大影响。

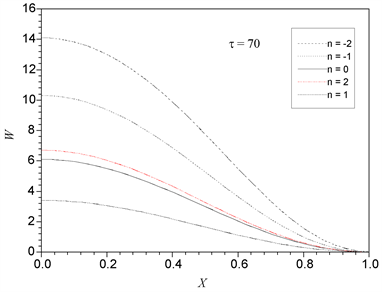
Figure 6. Configuration of clamped foam plate for different values of n

图6. 不同梯度下固支板的构形

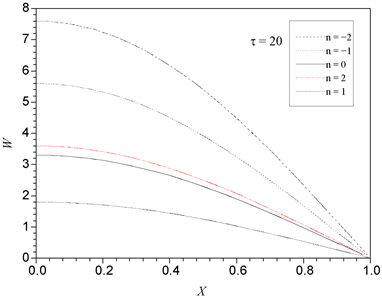
Figure 7. Configuration of simply supported poam plate for different values of n

图7. 不同梯度下简支板的构形

4. 结论

本文分别研究了温度载荷作用下，梯度泡沫材料圆板的轴对称过屈曲行为。研究结果表明：

1) 泡沫梯度指数为负值时，随着梯度指数的增加，板的临界载荷增加；梯度指数为正值时，随梯度指数增加，临界载荷减小。梯度指数负值时的临界载荷小于梯度指数为零时的临界载荷；梯度指数正值时的临界载荷大于梯度指数为零时的临界载荷。

2) 过屈曲后，随热载荷的增加，梯度泡沫板的过屈曲行为与各向同性均匀板有很大区别，说明出泡沫梯度板的力学响应与其材料的梯度的强相关性。

3) 固支板的临界载荷大于简支板的，两种边界下板的过屈曲构形图也不相同，可见，边界条件对梯度泡沫板的稳定性也有显著影响。