供热直埋热水管道弯管的整体与局部应力分析

Integral and Local Stress Analysis of Bend Pipe in Direct Buried Hot Water Heating Pipelines

摘要: 城镇供热直埋热水管道局部元件如弯头和三通等受力复杂，采用ANSYS进行建模可以得到详细的应力状态分析。大型管道系统线路长，架空管道和埋地管道混合在一起，建立全尺寸的ANSYS模型不具有可操作性。START管道应力分析软件采用一维梁模型经典管道应力分析模型理论，在大型管道系统长管段模拟上优势明显。为验证其可靠性，本文对比了START软件与ANSYS软件对供热直埋热水管道弯头应力分析的结果，分析了弯头一次以及二次应力随管道内压、埋深、壁厚、曲率半径、转角的变化规律。对比结果表明，START软件在直埋热管管道弯头应力分析上可以得到与ANSYS一致的结果，并且建模方便、计算迅速，可为直埋供热管道弯头的整体与局部应力分析提供帮助。

Abstract: Local components of the directly buried hot-water heating pipelines, such as bends and tee joints, bear complex stress which can be obtained by detailed stress state analysis using ANSYS simulation. However, it is not operable to establish detailed full-scale ANSYS models for large-scale piping systems which combine long overhead pipelines and buried pipelines. START Pipe Stress Analysis Software, which is based on one-dimensional beam model for classical pipe stress analysis, has obvious advantages for pipe stress analysis on large-scale piping systems with long pipelines. To verify the feasibility of START model, we conducted stress analysis of bend pipe indirectly buried hot-water heating pipeline by using START model and ANSYS model, respectively. The influences of the internal pressure, buried depth, pipe wall thickness, radius of curvature and angle of the bend on the primary stress and the secondary stress of the elbow were analyzed. The simulation results show that the START model obtains consistent results with the ANSYS model in the stress analysis of bend pipes. The START model, which is characterized by convenience for modeling and high computational efficiency, can provide help for integral and local stress analysis of bend pipe in direct buried hot water heating pipelines.

1. 引言

我国建筑能耗已占社会总能耗的20.6% [1]，供热用能是建筑能耗的重要组成部分。大型管网是集中供热系统的核心，其安全性尤为重要。目前，集中供热管网主要采用直埋敷设方式，弯头作为薄弱环节，通常会产生应力集中，引起局部范围内的循环塑性变形，经历一定运行周期后，产生疲劳破坏 [2]，影响管道安全。

目前，国内研究者多是基于ANSYS软件对非全尺寸管段内的弯头进行应力分析。

李明强、梁鹂、姚红等 [3] [4] [5] 采用SOLID单元建模分析了补偿弯臂长度、曲率半径对90˚Z形管段被补偿弯臂长度的影响。李海冬等 [6] 采用梁单元分析了90˚Z形管段弯臂处的位移，并以该位移作为约束条件，分析了单个弯头的应力分布。平飞等 [7] 采用SOLID单元和SURF154分析了非90˚Z形管段弯管的应力变化规律。刘桢彬等 [8] 对小管径等臂长L形弯管进行数值模拟，验证了模型及其边界条件的合理性。江超等 [9] 用壳单元分析了等臂长L形弯管的应力变化规律。徐钱等 [10] [11] 采用流–热–固耦合方法建立不等臂长L形弯管模型，得出不同位移释放量对弯头应力和变形量的影响，压力和温度分别作用和同时作用时弯管的应力分布。

以上研究为弯头局部详细应力分析提供了方法。在此基础上，为了研究弯头所在管系对弯头应力状态的影响，本文用START软件 [12] 建立管系全尺寸模型，计算得到了弯头的应力状态，分析了弯头应力状态的主要影响因素及应力变化规律。以弯臂处的位移值作为ANSYS弯头模型的边界条件，验证了START软件在供热直埋热水管道弯头应力分析中的可靠性。

2. 弯头整体应力分析

2.1. 直角弯头模型

管道物理模型如图1所示。F_r为弯头管段所受土壤和自身弹性力的作用而产生的反力；F为臂端处的轴力；F_f是管道所受土壤的轴向摩擦力；F_c是土壤对弯头及附近管道的横向压缩反力；W_t是管顶土压力；W_p是管道自重；W_b是管底土压力；F_w是土壤对管道的竖向作用力。

$Fw=Wb+\left(Wp+Wt\right)$ (1)

用START软件对水平敷设等臂弯头管段建模(图2)。弯头两臂长均为L = 500 m，工作压力P_n = 1.0 MPa，安装温度T₁ = 10℃，操作温度T₂ = 130℃，管顶覆土h = 1.5 m。在弯臂端分别设置固定墩。经过软件模拟分析后，发现在固定墩签的直管段上产生了锚固段，因此该模型可以代表无限臂长弯头，可视为全尺寸模型。

Figure 1. Physical model of bend pipe

图1. 弯头管段物理模型

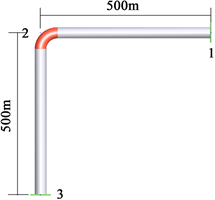
Figure 2. Right-angled bend pipe with arm length of 500 m

图2. 臂长500 m的直角等臂弯头管段

管道几何及材料参数见表1，土壤参数见表2。

Table 1. Pipe geometry and material parameters

表1. 管道几何及材料参数

Table 2. Pipe geometry and material parameters

表2. 回填土参数

土壤静压力系数计算公式如下 [13]：

$k_0=1-\sin \varphi$ (2)

式中：k₀为土壤静压力系数；φ为土壤内摩擦角(˚)。

土壤孔隙比与土壤容重和土壤颗粒比重的关系如下 [14]：

$e=\left(1-\frac{\gamma }{G_s}\right)\times 100\%$ (3)

式中：e为孔隙比；γ为土壤容重，kN/m³；G_s为土壤颗粒比重，kN/m³。

在上述公式(2)和(3)中，可分别计算出土壤静压力系数为0.5，土壤容重为9.13 kN/m³。

结合聚氨酯保温管道的特性和直埋土壤特性及相互作用关系，START软件自动建立土壤约束下的管道模型(图3)。其土壤的非线性刚度见下图4：

(a) (b)

Figure 3. (a) Finite element model of pipe and soil; (b) Soil simulation

图3. (a)管道与土壤的有限元模型；(b) 土壤模拟示意图

Figure 4. Nonlinear stiffness of soil

图4. 土壤的非线性刚度

2.2. 弯头应力分析

用Start-Prof软件分别对转角角度θ为90˚~170˚范围内的直埋供热弯管进行数值模拟，分析不同折角对弯管的一次应力和二次应力的影响特性。管道处于不同状态下的应力如图5所示。

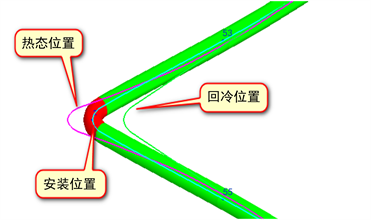
Figure 5. Stress distribution of bend pipe under installation, operation and cooling state

图5. 弯头管段的安装、运行和回冷状态应力图

2.2.1. 弯头一次应力变化规律

一次应力主要是在管道承载着内压和持续的外载作用下产生的，影响管道一次应力的因素有内压、壁厚、弯头曲率半径和管道埋深。

弯头一次应力随着壁厚的增加而降低，随内压的增加而增加；壁厚对弯头一次应力的影响规律呈线性变化(图6)。一次应力随着埋深的增加而增加，但不受曲率半径的影响(图7)。弯头一次应力随转角的增加先增加，角度大于160˚时，继续增大转角角度，则一次应力开始减小(图8)。

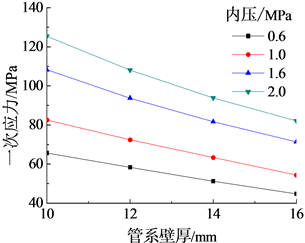
Figure 6. Influence of internal pressure and pipe wall thickness on primary stress

图6. 内压和管道壁厚对一次应力的影响

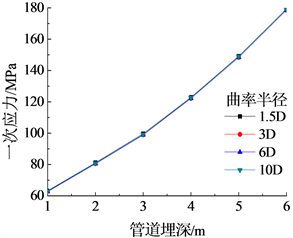
Figure 7. Influence of buried depth and curvature radius on primary stress

图7. 埋深和曲率半径对一次应力的影响

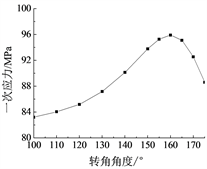
Figure 8. Influence of bend angle on primary stress

图8. 转角角度对一次应力的影响

埋地管道一次应力主要是管道在土壤外压，管道内压作用下的挤压瘪化所引起的，START软件考虑了内压作用下布尔登作用效果(弯头在内压作用下变直，管道拉长效果)，确保埋地管道在持续载荷作用下的安全。

从上面结果看，由于壁厚加大，管道抗弯、抗瘪化能力加强，一次应力减小；内压增大，管道挤压瘪化程度大，一次应力增大。

埋深加大，外压作用加强，一次应力加大；弯头曲率半径与弯头柔性及应力增大系数SIF有关，而一次应力与疲劳柔性无关，所以一次应力不受曲率半径的影响。

改变转角角度，在压力布尔登作用下，弯头压力硬化导致一次应力的变化，但相对变化幅值较小。

2.2.2. 弯管的二次应力影响因素

二次应力主要是由于管道热胀冷缩、纯温度导致管道变形，而变形受限所产生的应力，影响管道二次应力的因素不仅有内压、管道壁厚、弯头曲率半径和管道埋深，还有温升。

二次应力随内压、壁厚的增加而增加(图9)，随管道埋深、曲率半径的增加而降低(图10)，随温度的增加而增加(图11)，随转角角度的增大先增大后减小(图12)。

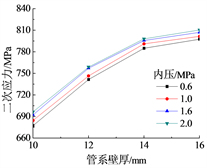
Figure 9. Influence of internal pressure and pipe wall thickness on secondary stress

图9. 内压和管道壁厚对二次应力的影响

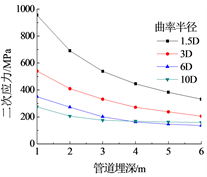
Figure 10. Influence of buried depth and curvature radius on secondary stress

图10. 埋深和曲率半径对二次应力的影响

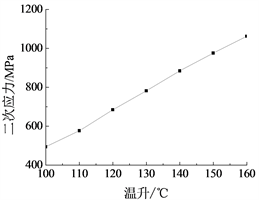
Figure 11. Influence of temperature rise on secondary stress

图11. 温升对二次应力的影响

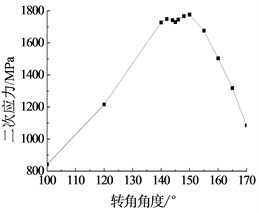
Figure 12. Influence of bend angle on secondary stress

图12. 转角角度对二次应力的影响

从上面结果看，壁厚增加，管道抗弯能力加大，柔性减弱，弯矩加大，导致二次应力增加。

弯曲半径增大，管道柔性变差，应力增大系数SIF降低，二次应力减小。

温升提高，弯头变形加大，弯矩加大，二次应力增加。

转角角度影响弯头K柔性系数和应力增大系数SIF，小折角最为不利，图示可以直管看到。

3. 弯头局部应力分析

3.1. 局部应力分析模型

在ANSYS软件中，选择Shell181单元对局部直角弯头进行建模。弯头两边直管臂长取40 m，模型的网格划分类型采用映射划分，为较为全面的得到弯头处的应力分布，在弯头区域进行网格加密。

管道与土壤之间的相互作用力用土弹簧来模拟，管道顶部加轴向土弹簧，模拟土壤对管道的摩擦力作用；管道左右两侧加横向土弹簧，模拟土壤对管道的横向压缩反力；管道底部加竖向土弹簧，模拟土壤对管道的竖向作用力；弯头外侧加2个不同方向的横向土弹簧(图13)。管道各方向土弹簧计算方式可由文献 [15] 中所给出的来进行计算，本文取管道和土壤的摩擦系数为0.4 [13]。在有管–土弹簧的基础上，先对仅有内压(1.0 MPa)荷载作用下的管道进行建模，再对增加温度(130℃)荷载后的管道进行建模，最后分别对这二种工况进行模拟，分析弯头应力分布规律。

3.2. 局部应力分析结果

仅在内压作用下，由START计算得到弯臂40 m处的轴向位移为1.5 mm。将上述位移值作为边界条件施加在图10模型的弯臂端点上，经ANSYS软件计算得到最大应力值出现在弯头顶部上，为59.7 MPa，弯头内拱处的当量应力值相对较小，靠近弯头外拱处的应力值最小，为26.7 MPa (图14)。

Figure 13. Local model of right-angled bend

图13. 直角弯管局部模型

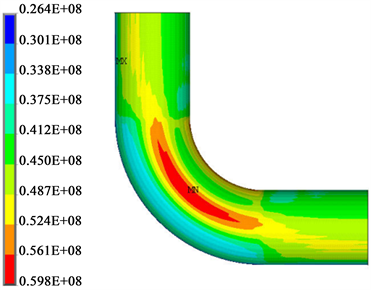
Figure 14. Stress distribution of bend pipe with internal pressure of 1.0 MPa

图14. 内压为1.0 MPa的弯头应力图

增加温升荷载，经START计算得到弯臂40 m处的轴向位移和侧向位移分别为91.5 mm和1.8 mm。将上述位移值作为边界条件施加在图10模型的弯臂端点上，经ANSYS软件计算得到最大应力值出现在在弯头顶部上，为672 MPa (图15)。

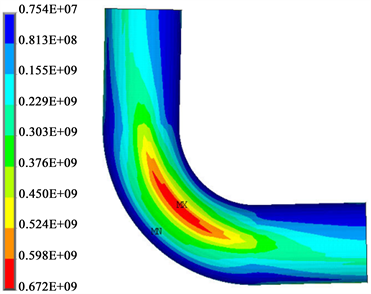
Figure 15. Stress distribution of bend pipe under 130°C

图15. 工作温度为130℃的弯头应力图

START计算仅内压作用下弯头处的最大当量应力为82.66 MPa，增加温升荷载后，最大当量应力为684.65 MPa。ANSYS计算仅内压作用下和增加温升荷载后的弯头最大当量应力分别为59.7 MPa、672 MPa。增加温升荷载后，两当量应力误差仅为2%，证明START软件和ANSYS软件的数值分析结果相吻合。

4. 结论

本文用START管道应力分析软件对全尺寸弯管进行建模，分析了弯头应力的变化规律和影响因素，并将结果与ANSYS计算结果进行了对比验证。通过计算模拟分析，得出如下结论。

1) 仅在内压和持续的外载作用下，弯头一次应力随内压、埋深的增加而增加，随着壁厚的增加而降低；在同种工况下，曲率半径几乎不对弯头的一次应力产生影响。

2) 增加温升作用后，弯头二次应力随着内压、壁厚的增加而增加，随埋深、曲率半径的增加而降低。

3) 随转角角度的增大，弯头的一次应力和二次应力大致均先增大后减小，当转角角度大于160˚时，一次应力开始逐渐减小，当转角角度大于150˚时，二次应力显著减小；弯头二次应力随温升增加而显著增加，其变化规律近似呈线性变化。

4) 采用一维梁单元有限元管道模型进行供热直埋管道应力分析，考虑聚氨酯保温管，土壤约束相互作用特性，考虑弯头柔性K和应力增大系数SIF的作用和影响，可以精准、快捷地对管道应力分析问题进行分析。

NOTES

^*通讯作者。