1. 引言
粒子群优化(Particle Swarm Optimization, PSO)算法是由Kennedy和Eberhart于1995年率先提出的,源于对鸟群或鱼群捕食过程的模拟。目前,粒子群优化算法已经在多个领域中得到应用 [1] [2] [3] [4] [5]。
Nash证明了n人非合作博弈Nash平衡的存在性 [6],但迄今未有通用算法来求解所有的博弈模型。Nash平衡的求解,最终可归结为求解一个约束优化问题,要得到此优化问题的准确解通常是很难的。然而在许多实际问题中,我们必须得到此优化问题的一个具体的解。一般采用某些数值方法求其近似,但数值方法通常要求可导、连续等条件。另一类方法是采用智能算法,这些算法直接对结构对象进行操作,不要求可导、连续等条件,它们具有内在的并行性和较好的寻优能力,可以自动调整搜索方向,从而较好地得到优化问题的解。目前,已有多种智能算法用来求解Nash平衡,包括遗传算法 [7]、启发式搜索算法 [8]、免疫算法 [9]、粒子群算法 [5] 及一些改进的粒子群算法 [10] [11] 等。
注意到一方面,求解优化问题时,智能算法后期收敛速度较慢,且容易陷入局部最优;另一方面,粒子群优化算法容易实现,将之作为博弈演化模型,能够比较合理地解释局中人的行为,即局中人是理性的,其目标是最大化自己的收益。本文以粒子群算法为基础,引入遗传算法的杂交算子,设计了一个求解Nash平衡的混合粒子群优化算法。实验表明,本文算法的收敛速度优于目前已有的一些算法。
2. 问题描述
设在一个n人非合作博弈G中,局中人
的纯策略集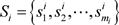 ,其中,
是局中人i的纯策略的个数,局中人i的支付函数为
。称
,其中,
是局中人i的纯策略的个数,局中人i的支付函数为
。称 为局中人i的一个混合策略,其中
为局中人i的一个混合策略,其中 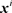 满足
,
,即纯策略集
上的一个概率分布。记局中人i的混合策略集记为
。博弈的混合策略组合可记为
。在此混合策略组合下,局中人
的期望支付
。
满足
,
,即纯策略集
上的一个概率分布。记局中人i的混合策略集记为
。博弈的混合策略组合可记为
。在此混合策略组合下,局中人
的期望支付
。
定义1 [12] 设
是n人非合作博弈G的一个混合策略组合,如果对任意
及
,均有
,则称
是博弈G的一个混合策略Nash平衡,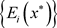 为对应的平衡结果。这里
为对应的平衡结果。这里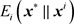 是将局中人i的混合策略
换成混合策略
是将局中人i的混合策略
换成混合策略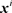 后的期望支付。
后的期望支付。
注意到局中人i的纯策略
等同于混合策略
,其中第k个分量为1,其余分量为0。Nash平衡具备重要性质 [5]: 是n人非合作博弈G的一个混合策略Nash平衡的充要条件是:对于每个局中人i及每个纯策略
,有
。
是n人非合作博弈G的一个混合策略Nash平衡的充要条件是:对于每个局中人i及每个纯策略
,有
。
特别地,对双矩阵博弈
(简记
),其中,
分别为局中人1与局中人2的混合策略,
是
维支付矩阵,即
与
分别为局中人1采取混合策略
、局中人2采取混合策略
时,局中人1与局中人2的期望支付。
本节余下内容,我们将求解Nash平衡问题转化为优化问题。
我们给每个混合策略组合赋予一个适应度。对混合策略组合
,根据Nash平衡的定义与性质,定义
的适应度
,这里
为局中人i关于混合策略组合
的适应度,
为所有局中人关于混合策略组合
的适应度之和。由Nash平衡的性质,混合策略组合 为纳什均衡解当且仅当适应度函数在
处取得最小值0。故博弈的混合组合空间内只有Nash平衡点的适应度最小。
为纳什均衡解当且仅当适应度函数在
处取得最小值0。故博弈的混合组合空间内只有Nash平衡点的适应度最小。
特别地,对双矩阵博弈
,其中
是
维支付矩阵, 混合策略组合
的适应度
如下:
其中,
为矩阵A的第i行所对应的向量,
为矩阵B的第j列所对应的向量。
3. 混合粒子群算法设计
在粒子群算法中,优化问题的任一可行解都是搜索空间中的一个粒子,每个粒子都有一个由目标函数所确定的适应度。粒子群算法首先初始化一群随机粒子(包括初始位置及速度),然后这些粒子追随当前的最优粒子在搜索空间中随机搜索,最后通过迭代找到近似最优解 [13]。
每个粒子在搜索时,根据自己的速度、自己搜索到的历史最好点与群体内其他粒子的历史最好点,进行位置与速度的更新。记
为第i个粒子的位置,
为第i个粒子的速度,
为第i个粒子经过的最好点,
为群体内所有的粒子经过的最好点。一般地,粒子的位置和速度都在连续的实数空间内取值。在粒子群算法的迭代中,第i个粒子的速度与位置的更新公式如下:
(1)
(2)
其中,
是第i个粒子在第k次迭代时的速度, 是第i个粒子在第k次迭代时的位置。
是惯性权重,大小决定了对粒子当前速度继承的多少;
是
是第i个粒子在第k次迭代时的位置。
是惯性权重,大小决定了对粒子当前速度继承的多少;
是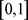 区间内的随机数,
区间内的随机数,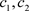 是学习因子。粒子的速度被限制在一个最大速度
的范围内。
是学习因子。粒子的速度被限制在一个最大速度
的范围内。
杂交(交叉)是遗传算法中的一个非常重要的遗传算子,它同时对两个染色体进行操作,组合二者的特性产生新的后代。遗传算法的性能在很大程度上取决于采用的杂交运算的性能。可将杂交算子引入粒子群算法中,基于这一思想,我们设计了一个求解博弈Nash平衡的混合粒子群算法。
在算法中,粒子就是一个混合策略组合,算法如下:
Step 1确定学习因子
,群体规模N,最大迭代代数
,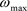 ,
及精确度
。
,
及精确度
。
Step 2随机初始化粒子群及其速度,使每个粒子的第i个向量满足
每个粒子速度的第i个向量满足
。
Step 3计算各个粒子的适应度,并对粒子按照适应度大小进行排序,适应度小的一半粒子直接进入下一代
(另一半记为
),对适应度大的一半粒子进行杂交,杂交之后先对粒子作归一化处理,使之满足
;并与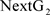 形成粒子池,计算粒子池中粒子的适应度,选择适应度小的一半粒子与
形成下一代粒子
。
形成粒子池,计算粒子池中粒子的适应度,选择适应度小的一半粒子与
形成下一代粒子
。
Step 4计算当前粒子群
中粒子的适应度值及
, 并把
作为记忆粒子存入记忆库中。
Step 5判断是否满足
或
。 若满足,则停止并输出迭代次数
以及
的适应值;否则,继续。
Step 6利用公式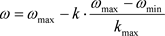 计算惯性权重
。
计算惯性权重
。
Step 7按公式(1)与(2)更新
中粒子的速度与位置。
Step 8依次检验第i个粒子
是否属于
。否则,计算控制步长
(此技术来自文献 [11]),并令
,然后作归一化处理,使得
回到混合策略组合空间中,形成新一代粒子群体
。然后转到第3步。
关于算法的性能,本文以算法获得Nash平衡或其近似解的平均迭代次数来度量。
4. 数值例子
本文用文献 [9] [10] 中给出的4个经典的
博弈和一个
博弈(例1~5)以及文献 [7] [10] [11] 中共同给出的一个
博弈(例6)作为算例,用本文给出的混合粒子群算法求解这些博弈。
例1 囚徒困境博弈
,其中,
,
;
例2 智猪博弈
,其中,
,
;
例3 猜谜博弈
,其中,
,
;
例4 监察博弈
,其中,
,
;
例5 博弈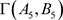 ,其中,
,
;
,其中,
,
;
例6 博弈
,其中,
,
。此博弈具唯一解
。
利用本文设计的混合粒子群算法求解上述博弈,例1~5中算法的参数设置为:群体规模
,学习因子
,最大迭代次数为1000,精度设置为
,其计算结果如表1~5所示。例6中精度设置为
,其余参数不变,计算结果如表6。

Table 1. Computing result of game Γ ( A 1 , B 1 )
表1. 博弈
的计算结果

Table 2. Computing result of game Γ ( A 2 , B 2 )
表2. 博弈
的计算结果

Table 3. Computing result of game Γ ( A 3 , B 3 )
表3. 博弈
的计算结果

Table 4. Computing result of game Γ ( A 4 , B 4 )
表4. 博弈
的计算结果

Table 5. Computing result of game Γ ( A 5 , B 5 )
表5. 博弈 的计算结果
的计算结果

Table 6. Computing result of game Γ ( A 6 , B 6 )
表6. 博弈
的计算结果
考虑算法的性能,即获得近似解的平均迭代次数。通过计算实验可知,用本文算法在适应函数精度
和群体规模
的情况下,例1~5的5次计算结果分别需要平均迭代2代、3 代、2代、7代和9代。在平均迭代次数方面,优于文献 [10] 用免疫粒子群算法给出的结果(文献 [10] 中例1~5在适应函数精度
的情形下,5次计算结果需要平均迭代7代、3代、4代、14代和15代),特别是例6(本算法在适应度函数精度
)情况下,5次的计算结果需要平均迭代为46,文献 [10] 在适应度函数精度为
,5次的计算结果需要平均迭288代),本算法有较大的改进,在计算过程中运行速度非常快。当然,本算法也优于 [9] 的算法。
5. 结束语
本文算法的目标在于找到博弈的一个Nash平衡或其近似解。但一个博弈中,可能存在多个Nash平衡,究竟哪个平衡才是最终的博弈结果,本文的算法并没有作这方面的考虑。进一步工作中,我们希望能够引入一些机制,使得算法找到的平衡点更接近与现实的博弈结果。此外,实验还表明,当局中人纯策略数增大时,算法的迭代次数呈指数增长。
致谢
感谢匿名审稿人对本文初稿提出的宝贵意见。
基金项目
贵州省教育厅青年科技人才成长项目(黔教合KY字[2017]225)。