1. 引言
随着桥梁行业的发展,为了满足更大跨越能力的要求,预应力混凝土构件孕育而生。预应力混凝土构件因其有较好的承载力、变形小、截面小、恒载小等优点,被广泛的使用于各类桥型之中。因此预应力混凝土构件的安全承载就称为了主要的探讨对象,大部分研究者 [1] [2] [3] [4] [5] 对预应力混凝土构件的极限承载力进行研究,主要分析了在荷载下构件的挠度、应变以及中性轴的变化过程。但对预应力混凝土构件承载力的影响参数研究较少 [6] [7] [8],且研究对象都为缩尺梁。为了进一步对预应力构件的承载力影响参数,本文以沈山高速某桥的施工标准图建立有限元模型,对影响承载力参数进行详细分析。
2. 主要影响参数
由公预规JTGD62-2012可知在截面一定时,受压区配筋、受拉区配筋、混凝土强度、受压区高度为影响梁体的极限承载力的主要因素。当构件截面高度一定时,影响混凝土受压区高度的因素主要有哪些。为了定性的探知受压区混凝土高度的影响因素进行如下推导,推导过程中运用了平截面假定和中性层理论。
设在初始张拉预应力和外荷载作用下截面下缘主拉钢筋应变为:
(1)
因此钢绞线,受压区钢筋、混凝土的应变分别为:
(2)
(3)
(4)
式中,
为钢绞线的初始张拉预应力。
由截面静力平衡方程可得
(5)
将公式(4~11)也可表示为如下形式
(6)
式中,
求解公式(6)可得梁体破坏时受压区高度
(7)
由以上公式可得,在加载过程中影响受压区高度变化的影响因素有,配筋率、张拉预应力、混凝土强度等级。
由以上分析得出了影桥梁承载力的因素,因此在下面章节中主要分析有效预应力、预应力比率PPR、混凝土强度等级、受压区高度系数对预应力连续矮肋T梁承载力的影响。
3. ABAQUS有限元模型
本梁为两跨预应力混凝土连续矮肋T梁,单跨跨径为16 m,截面高度为1050 mm,翼缘板宽度为1200 mm,跨中腹板宽度为240 mm。该T梁按预应力A类构件进行设计,设计荷载为公路–I级荷载,主要受力钢筋采用HRB400,钢绞线采用直径为15.20 mm (7A5)低松弛高强度钢绞线,混凝土等级为C50。通过ABAQUS建立有限元模型梁,如图1所示为左跨模型图,模型梁中钢筋本构采用规范《混凝土结构设计规范》(GB50010-2010) [9],钢绞线本构关系采用《预应力混凝土结构设计原理》,因模型中引入混凝土塑性损伤模型 [10],因此需引入塑性损伤因子。如表1所示为CDP模型损伤因子参数,表2为塑性破坏准则参数。


Table 1. CDP model damage factor parameter table
表1. CDP模型损伤因子参数表

Table 2. Parameter table of plastic failure criterion of CDP model
表2. CDP模型塑性破坏准则参数表
4. 有限元分析结果
4.1. 有限元模型认证
根据公预规中的开裂弯矩、极限弯矩计算方法,得出的结果与有限元计算结果进行对比,其对比结果如表3所示。由表3可知,对于开裂弯矩的计算,有限元计算结果与规范计算结果吻合度较高,达到了0.96。有限元计算得出的极限弯矩与规范计算值相差甚远,规范计算弯矩与有限元计算弯矩比值为0.66,但其接近钢绞线的抗拉强度设计值与极限强度标准值之比0.7,是因为规范对极限弯矩的计算采用设计值,而实际极限弯矩是由材料标准值决定。因此可得通过ABAQUS有限元模拟得出的结果与规范计算结果较为吻合。

Table 3. Comparison of cracking moment and failure moment
表3. 开裂、破坏弯矩对比表
4.2. 有效预应力
的影响
通过改变
,来分析其对梁承载力的影响。如表4为不同
下梁的承载力情况,从表4中可以处
的变化范围在795 MPa~1395 MPa之间,所对应的模型梁分别为B1~B5,如图3所示为B1~B5的荷载–挠度曲线图。
从表4中可以看出
从795 MPa变化到1395 MPa时,梁的正常使用极限荷载从372 kN增加到了660 kN,提高了77%;梁的承载能力极限荷载从1176 kN增加到1200 kN,提高了2%;梁的极限位移从235 mm减小到121 mm,减小了48.5%。从图2中可以看出随着
的增长,同级荷载下梁的位移有较为明显的减小。产生以上结果的原因主要是:预应力的施加使梁体跨中下缘和中支座上缘产生压应变储备,这就使得必须用部分外荷载来抵消压应变储备,从而推迟梁达到正常使用极限荷载,因此所施加的预应力越大梁的正常使用极限荷载也就越大;预应力的张拉只是使预应力筋提前处于一种受力状态,提高梁体的使用性能,但不能提高预应力筋的抗拉强度,因此张拉预应力筋对梁的承载能力极限荷载影响较小;当预应力越大,受压缘处的压应变储备也就越大,在相同外荷载作用下,梁抵抗变形的能力也就越大,因此预应力越大,同级荷载下梁的位移有较为明显的减小。综上可知:
的增加对梁的承载能力极限荷载影响较小,但对梁的正常使用极限荷载影响较大,且可以减小梁在各级荷载下的位移,因此
的提高可加强梁的安全承载。

Table 4. Influence of initial prestress on bearing capacity
表4. 初始预应力对承载力的影响
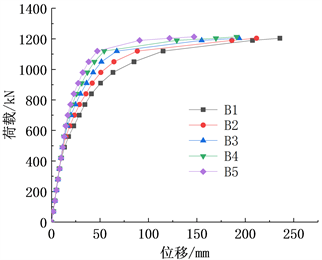
Figure 2. Load displacement curve of beam B1 - B5
图2. B1~B5荷载–位移曲线
4.3. 预应力比率PPR的影响
预应力比率由A. E. Naaman提出,可用下列公式表达:
(12)
式中:
为预应力筋提供的极限抗弯承载力;
为预应力和主筋提供的极限抗弯承载力之和。
如公式(13)可知,改变主筋截面或预应力筋截面会使PPR发生变化,但也会改变受压区高度系数ξ,但同时改变两者可使ξ保持不变。本小结通过保持受压区高度系数ξ不变,改变预应力比率PPR,来研究PPR对预应力连续梁承载力的影响。
(13)
如表5所示为预应力比率在0.6~1.0变化下,相对应梁B6~B10的承载力状况。如图3所示为梁B6~B10荷载–位移曲线。

Table 5. Influence of PPR on bearing capacity
表5. 预应力比率PPR对承载力的影响
从表5中可以得出,当PPR从0.6增加大1.0时,梁的正常使用极限荷载从430 kN增加到了855 kN,提高了98%;梁的承载能力极限荷载在呈现先减小,后增加的趋势,谷值出现在PPR = 0.9时,谷值与最大值之间仅相差5.3%;梁的极限位移从147 mm增加到了189 mm,增加了28%。产生以上结果的主要原因:随着PPR的增加,预应力筋面积相应增加,因此梁的受拉缘压应力储备也相应增加,由4.2可知,梁的正常使用极限荷载也随着增加;随着PPR的增加,钢筋截面也随着减小,由钢筋与预应力筋设计强度之比,可知钢筋截面减小量是预应力筋截面增加量的3.7倍;因此随着PPR的增加,受拉筋配筋率在急剧减小,因此梁极限位移在随之增大。由此可知,预应力筋的使用极大的减小梁内了钢筋用量。
从图3中可以看出随着PPR的增加,荷载在770 kN之前;梁B10的位移在同级荷载下相对其他各梁的增加较快,主要是因为B10中没有下缘受拉钢筋,因此可知对于预应力A类以上构件配置下缘受拉钢筋,在设计荷载内可以减小梁体位移;荷载在100 kN之前,梁B6~B9的位移在同级荷载下基本相同,因此可知对于预应力A类以上构件,配置下缘受拉钢筋适量即可;当荷载在1100 kN之后B7梁的位移相对各梁增加较快,但不会影响预应力A类构件的正常承载。综上所述:PPR的提高,对梁的承载能力极限荷载的影响较小,对梁的正常使用极限荷载有较大的提高;但PPR的取值应小于1,当PPR = 1时,并不利于梁的承载。

Figure 3. Load displacement curve of beam B6 - B10
图3. B6~B10荷载–位移曲线
4.4. 混凝土强度等级的影响
由规范 [9] 可知,
(14)
因此,相邻混凝土等级下的受压区高度x之比:
(15)
因此可得,相邻混凝土等级下的弯矩之比:
(16)
当
时,
(17)
如表6所示为混凝土改变对梁承载力的影响,混凝土变化范围在C40~C80之间,所对应的梁为B11~B15,如图4所示为梁B11~B15的荷载–位移曲线。

Table 6. Influence of concrete strength grade on bearing capacity
表6. 混凝土强度等级对承载力的影响
从表6中可以看出混凝土强度等级从C40上升到C80后,梁的正常使用极限荷载从594 kN提高到612 kN,提高了3%;梁的极限荷载1212 kN提高到了1280 kN,提高了5%;极限位移从173 mm下降到145 mm,减小了16%。产生以上结果的主要原因:随着混凝土强度等级的增加,混凝土轴线抗压强度变大,受压区高度x减小,相应
增大,因此对梁的承载能力有相应提高,但由公式(17)可知梁的承载能力提高较小。从图4中可以看出混凝土强度等级的提高对正常使用荷载范围内梁的位移减小较少,但可以较大减小梁开裂后的位移,其原因是因为随着混凝土等级的提高,混凝土弹性模量也会随之增加,梁的抗弯刚度也会随着增加。综上所述,混凝土强度的提高对梁的承载力影响较小,非特殊混凝土构件不推荐采用高强度混凝土。

Figure 4. Load displacement curve of beam B11 - B15
图4. B11~B15荷载–位移曲线
4.5. 受压区高度系数ξ的影响
根据公式(13)可知,在混凝土强度等级不变的情况下,影响受压区高度系数ξ的因素主要有三个:受拉主、钢绞线、受压钢筋的配筋率。为了因素分析的简单化,将受压筋分为一组,将受拉筋分为一组,受拉组在保证PPR不变的情况下改变受拉区配筋率,具体情况见表7所示。

Table 7. Change table of height coefficient ξ in compression area
表7. 受压区高度系数ξ变化表
如表8为受拉区配筋变化下,受压区高度系数ξ对梁承载力的影响情况,受压区高度系数变化范围为0.093~0.139,对应的梁分别为B16~B20,如图5为梁B16~B20的荷载–位移曲线图。

Table 8. The influence of ξ on bearing capacity
表8. ξ对承载力的影响
从表7、表8中可以看出受拉区配筋率的增加会导致受压区高度系数的增加,随着受压区高度系数的增加,使梁的正常使用极限荷载从504 kN提高到了768 kN,提升了52%;使梁的承载能力极限荷载从1144 kN提高到了1472 kN,提升了28%,对梁的极限位移影响并无规律。从图5中可以看出受压区高度系数的增加,可以明显的减小梁在同级荷载下的位移。综上可知,由受拉区配筋率增加导致的受压区高度系数的增加,对梁的承载能力有较大提高。

Figure 5. Load displacement curve of beam B16 - B20
图5. B16~B20荷载–位移曲线
如表9为受压区配筋变化下,压区高度系数ξ对梁承载力的影响情况,受压区高度系数变化范围为0.105~0.117,对应的梁分别为B20~B25,如图6为B20~B25的荷载–位移曲线图。

Table 9. The influence of ξ on bearing capacity
表9. ξ对承载力的影响

Figure 6. Load displacement curve of beam B20 - B25
图6. B20~B25荷载–位移曲线
从表7、表9中可以看出受压区配筋率对受压区高度系数ξ的影响较小,且随着受压区配筋率的减小ξ在增大。随着ξ的增加,梁的正常使用极限荷载没有变化;梁的承载能力极限荷载也影响较小,仅减小了1%;梁的极限位移从148 mm增加到了170 mm,减增加了15%。产生以上结果的原因:受压钢筋因的减小,会使
有所减小,因此受压筋的变化会影响梁的承载力,但因受压筋的配筋率较小,因此,受压筋的变化对梁的承载力影响极小。从图6中可以看出受压区高度系数的增加,在正常使用荷载下对梁的位移基本并无影响。综上可知,由受拉区配筋率变化导致的受压区高度系数的增加,对梁的承载能力影响较小。
5. 结论
本文通过ABAQUS有限元软件的控制参数法,对32 m两跨预应力混凝土连续矮肋T梁进行模拟,分析影响预应力混凝土承载力的主要参数,所得结论如下:
1) 有效预应力对矮肋T梁的承载能力极限荷载影响较小,但对矮肋T梁的正常使用极限荷载影响较大,且可以有效的减小梁在各级荷载下的位移,因此有效预应力的提高可加强梁的安全承载。
2) 预应力比率PPR的提高,对矮肋T梁的承载能力极限荷载的影响较小,对矮肋T梁的正常使用极限荷载有较大的提高;PPR的增加可减小截面配筋率,但PPR的取值应小于1,当PPR = 1时,并不利于梁的正常承载。
3) 混凝土强度的提高对矮肋T梁的承载力影响较小,但可增大梁的抗弯刚度,减小梁在同级荷载下的位移。
4) 梁受拉区配筋率的增加或受压区配筋率的减小,都会使受压区高度系数增加。前者导致的受压区高度系数的增加,对矮肋T梁的承载能力有较大提高;后者导致的受压区高度系数的增加,对矮肋T梁的承载能力影响较小。
NOTES
*通讯作者。