1. 引言
叶片作为叶轮机械设备中的关键单元，其性能的优劣很大程度上决定了设备的整体性能。如何设计出高效、低噪的叶片一直是备受人们关注的问题。经过近百年的研究，众多学者发现 [1] [2] [3] [4] [5]，叶片几何结构是影响叶片气动、噪声特性的重要因素之一，并指出叶片的相对厚度、相对弯度与叶片绕流特性及其辐射的气动噪声密切相关。
冉景洪和刘子强等 [6] [7] 实验研究了相对厚度、相对弯度对低雷诺数下飞行器叶片气动特性的影响规律，研究表明最大相对弯度位置的影响大于最大相对弯度，最大相对弯度位于40%弦长附近表现出最优气动特性，叶片相对厚度越小越易获得较好的气动特性。R. Sankarasubramanian等 [8] 选择相对厚度分别为12%、15%、18%和30%的NACA对称叶片为研究对象，研究相对厚度对叶片气动特性的影响，指出叶片相对厚度是影响低斯特劳哈尔数下叶片气动性能的主要因素，合适的相对厚度会使叶片升力系数提高约30%。贾亚雷和安鹏等 [9] 以实验和模拟相结合的方式研究不同相对厚度对DU系列叶片气动性能变化的规律，结果表明叶片升阻比、最大升力和失速对应攻角都受到叶片相对厚度的影响。董青山和陈建 [10] 探究了轴流风机叶片相对厚度和相对弯度对风机气动性能的影响，研究发现相对厚度较小时气动性能较优，当风机流量较大时大弯度叶片表现出更好的气动性。张旭 [11] 通过数值模拟研究相对弯度分别为1%、2.5%和4.5%的钝锯齿尾缘叶片气动特性，结果表明随着相对弯度增大，升力系数呈先增后降的趋势，叶片升阻比呈上升趋势，相对弯度与叶片升力之间呈非线性关系，相对弯度为2.5%时叶片气动性能最优。孙振业 [12] 选取相对弯度1%、2%、3%和4%的NACA系列叶片为对象，研究叶片相对弯度对叶片气动噪声源和远场辐射噪声的影响，研究表明，相对弯度增大，叶片尾缘处辐射噪声会在低频段降低，并且主要噪声频率会向低频区域移动。
目前，关于几何参数影响研究的叶片载体多种多样，所得结论也各不相同，但针对降噪效果极佳的倾斜锯齿尾缘仿生叶片 [13] 鲜有研究，故本文以此类仿生叶片为基础，改变叶片相对弯度、相对厚度两个参数，通过数值方法探究这些几何参数对仿生叶片气动及噪声特性的影响规律，为仿生叶片进一步降噪、增升的优化设计提供参考及指导。
2. 数值计算方法
2.1. 几何模型及边界条件
本文以NACA65系列叶片为基础叶片，弦长C = 560 mm，展长B = 201.6 mm，参考文献 [14] 取相对齿宽λ/C = 0.12、相对齿高h/C = 0.06对叶片尾缘进行处理，再根据文献 [13] 构造倾斜锯齿，齿根线与中弧线夹角α取45˚，获得如图1所示的倾斜锯齿尾缘叶片。在此基础上，以叶片相对弯度、相对厚度作为自变量，最终形成5种不同几何参数的倾斜锯齿尾缘叶片，如图2所示。模型A、B和C相对厚度相同，相对弯度分别是：2%、4%和6%；模型C、D和E相对弯度相同但相对厚度不同，分别是：10%、14%和18%。叶片具体几何参数见表1。
(a) 锯齿尾缘叶片 
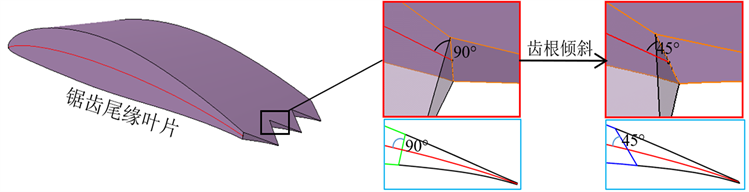(b) 倾斜锯齿齿根构造示意图
Figure 1. Inclined serrated trailing edge blades
图1. 倾斜锯齿尾缘叶片
Table 1. Blade geometric parameters
表1. 叶片几何参数
使用商业软件Fluent做叶片流场、声场的数值计算，来流工质为空气，基于弦长的雷诺数Rec = 105，由于进口马赫数(0.008)远小于0.3，故可认为流动是不可压缩的。定常计算采用SST k-ω双方程湍流模型，将收敛结果作为瞬态计算初始场，开启LES方程同时打开FW-H方程计算叶片绕流流场及辐射声场。给定速度入口，自由出流的边界条件，叶片展向为周期性边界条件，时间步长 t取10−4 s。
2.2. 网格划分及无关性验证
图3(a)为计算域示意图，进口距叶片尾缘10倍弦长，出口距叶片尾缘13倍弦长，高为18倍弦长。计算域分为远场外域和近场内域，外域为外部势流区，内域包括边界层及尾流区。内域采用O型拓扑划分网格，图3(b)展示了叶片近壁面处的边界层网格，为充分捕捉流动，对前、尾缘附近结构复杂、流动变化剧烈的区域进行局部加密。近壁面第一层网格高度 y取0.015 mm，由图3(c)中的叶片表面y+分布计算结果可知近壁区网格y+值被控制在1附近，满足大涡模拟的要求。
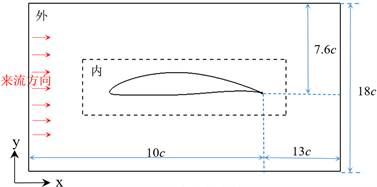(a) 计算域尺寸 
(b) 叶片近壁附近网格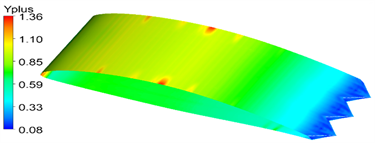 
(c) 叶片表面y+分布
Figure 3. Computational domain and mesh division information
图3. 计算域和网格划分
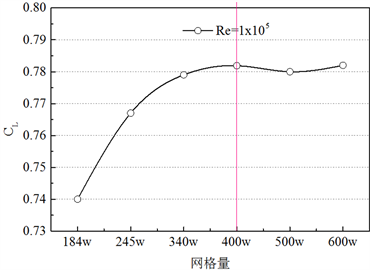
综合考虑计算资源的消耗和数值仿真的准确性，需要进行网格无关性分析和数值验证。共设计6套不同密度的网格，3˚攻角下叶片C升力系数CL随网格数量的变化曲线如图4(a)所示，随着网格数增加，升力系数呈先增加后小幅波动的趋势，当网格数达400万时，叶片升力系数变化幅度小于0.4%，此时可认为网格量对数值模拟的结果影响较小。该套网格的叶片表面静压系数模拟结果与实验对比如图4(b)所示，模拟值与实验值平均相差2.7%，分布基本吻合，故最终确定叶片网格总数在400万左右最为合适。
(a) 升力系数随网格总数的变化 
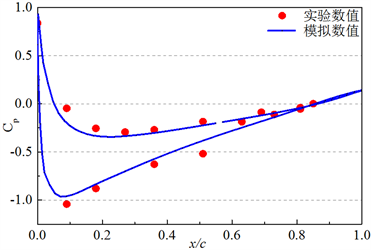(b) 表面静压系数可靠性验证
Figure 4. Grid independence and accuracy tests
图4. 网格无关性检验
3. 计算结果分析
3.1. 相对弯度、相对厚度对叶片气动特性的影响
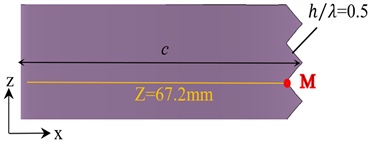
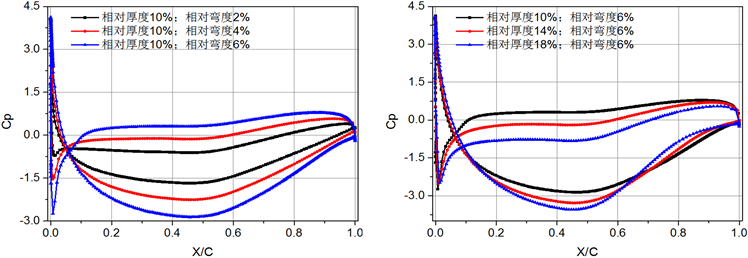
图5为0˚、6˚和12˚攻角下齿根位置处(图1中的M点)叶片表面静压分布。0˚攻角下，随着叶片弯度增加，叶片吸力面的压力降低，压力面的静压系数增大，故上下翼面静压曲线在图中所包围的面积增大，叶片气动性能得到提升，而叶片吸力面压力分布对叶片厚度的变化不敏感，具体表现为：当0.2 < X/C < 0.6时，厚度增加减小了叶片吸力面的压力，但当0.6 < X/C < 1时，厚度增加反而略增了吸力面的压力，叶片厚度的影响主要体现在压力面上，叶片越厚，压力面静压系数越小，叶片气动性能越差；6˚攻角下的叶片静压分布规律与0˚攻角的类似；12˚攻角下，除上述规律外，叶片弯度、厚度的影响主要集中在叶片吸力面前缘位置，增大弯度、减小厚度都能显著降低此处的静压系数，从而改善叶片的气动性能。
(a) 0˚攻角；相同厚度不同弯度(b) 0˚攻角；相同弯度不同厚度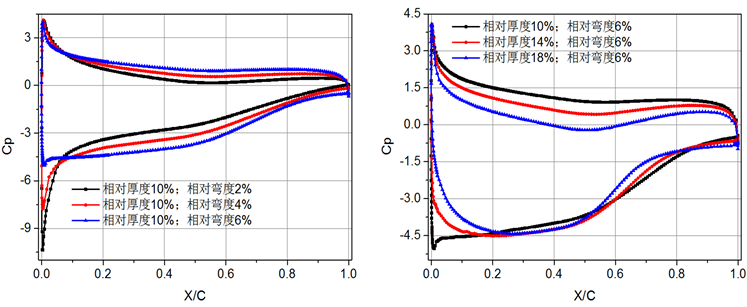 
(c) 6˚攻角；相同厚度不同弯度(d) 6˚攻角；相同弯度不同厚度
(e) 12˚攻角；相同厚度不同弯度(f) 12˚攻角；相同弯度不同厚度
Figure 5. Distribution of static pressure coefficient on blade surface
图5. 叶片表面静压系数
(a) 升、阻力系数；相同厚度不同弯度(b) 升阻比；相同厚度不同弯度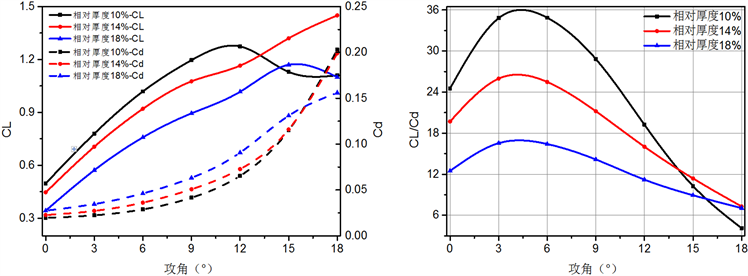
(c) 升、阻力系数；相同弯度不同厚度 (d) 升阻比；相同弯度不同厚度
Figure 6. Lift, drag coefficient and lift-to-drag ratio curve
图6. 升、阻力系数和升阻比曲线
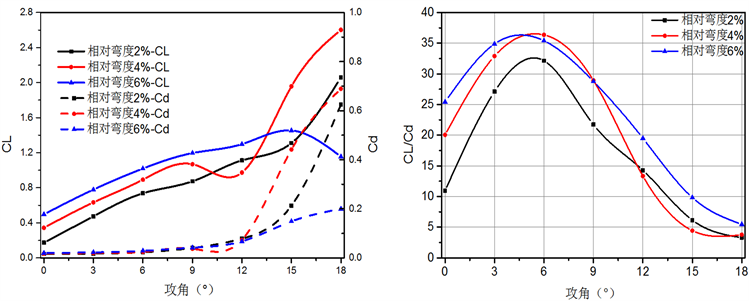
5种叶片模型的升、阻力系数和升阻比随攻角的变化曲线如图6所示。12˚攻角之前，叶片弯度增大，叶片升力系数增大，而阻力几乎不变，大攻角下，小弯度叶片的升、阻力系数曲线斜率猛增，而相对弯度6%的叶片阻力随攻角增加缓慢。这就使得在小攻角下，叶片弯度越大升阻比越大，气动性能越好，6˚和9˚攻角下，相对弯度4%的叶片能提供更大的升阻比，大攻角下，由于弯度大的叶片阻力下降明显，表现出的气动性能最佳。从叶片厚度的角度看，攻角小于12˚时，叶片升力系数随厚度增大而减小，阻力系数随厚度增大而增大，导致图6(d)中叶片升阻比随厚度增大明显降低的结果，而在大攻角下厚度小的叶片升力小、阻力大，气动性能反而不佳。
3.2. 相对弯度、相对厚度对叶片绕流、声辐射特性的影响
图6中各叶片升阻比均在6˚攻角附近达到峰值，故本文以此工况为代表工况，分析叶片几何参数对叶片绕流流场及声辐射特性的影响。
图7对比了倾斜锯齿尾缘叶片齿根处展向截面的压力云图。叶片弯度增大，吸力面低压区和压力面高压区范围扩大，且向尾缘延伸，上下翼面压差增大，叶片气动性能改善，图5(c)中的静压曲线分布印证了这一点；叶片厚度对吸力面的影响不大，主要是使吸力面上的低压区起始点后移，但厚度增大显著减小了压力面上靠近前缘的高压区域，削弱了叶片的气动性能，这与图5(d)中的静压曲线分布相符。
(a) 模型A (b) 模型B(c) 模型C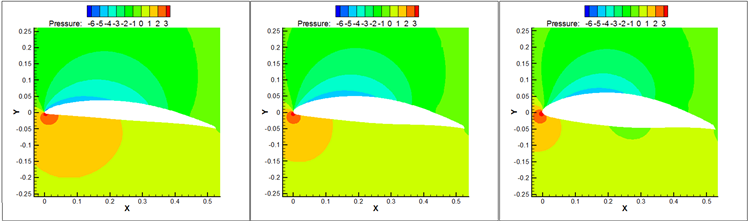
(d) 模型C (e) 模型D(f) 模型E
Figure 7. Pressure distribution of blade tooth root span wise section
图7. 叶片齿根展向截面压力分布
由边界层分离理论 [15] 可知分离点的判据为：
(1)
考虑到流动过程中的分离再附现象，取叶片表面上第一次出现壁面切应力为0的点作为分离点，图7中各叶片吸力面侧的分离点位置如表2所示：
Table 2. Position of separation point on blade surface
表2. 叶片表面分离点位置
叶片弯度、厚度增大均会使叶片分离点位置前移、流动恶化。模型A与模型E分离点位置差异最大，相差0.29 C。在叶片分离点前X/C = 0.6、分离点后X/C = 0.95处作各叶片边界层内的速度分布，如图8所示。以主流速度的99%作为边界层与主流区的边界，各叶片的边界层高度在每条曲线上用点来标识。由图8(a)知，分离点前的叶片边界层高度与叶片弯度成反比，弯度越大，边界层越薄，层内相应的速度
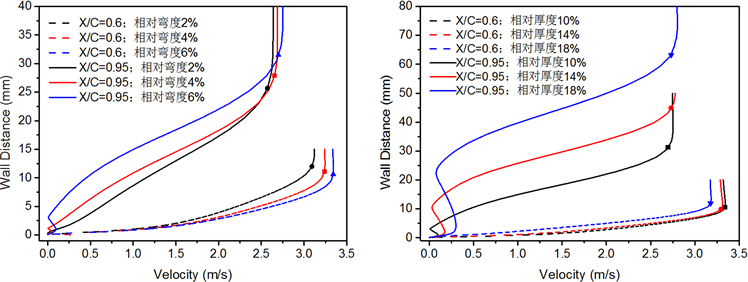(a) 厚度相同；弯度不同(b) 弯度相同；厚度不同
Figure 8. Velocity distribution in boundary layer
图8. 边界层内速度分布
梯度也越大，而在分离点后，边界层沿流向厚度增大，叶片弯度增大不仅会导致边界层加厚，还会使层内速度沿壁面法向产生扰动而非单调增加，流动稳定性减弱。图8(b)表明：叶片厚度对分离点前的边界层影响不明显，但此参数决定了分离点后的层内速度分布，叶片越厚，边界层也越高，层内速度扰动越剧烈，不稳定流动与叶片表面的相互作用增强，叶片辐射噪声能力也相应加强。
为了进一步阐释相对弯度、相对厚度对叶片绕流内部流场特性的影响，本文给出了各叶片在尾缘附近M点处的压力脉动分布，如图9所示。叶片表面压力脉动主要贡献频率集中在低频段，相对弯度、相对厚度增大均会增大压力脉动幅值，根据Curle对Lighthill声比拟拓展，声场产生包括四极子体分布和偶极子面分布，低雷诺数下，不稳定流动所致噪声为偶极子特性，在只关注偶极子源的情况下，削弱压力脉动有利于降低偶极子声源，故由图知模型A的偶极子声源强度最低；此外，各叶片脉动幅值所对应的频率发生频移，此频率与流场中尾涡脱落相关，表明叶片几何参数改变了叶片绕流过程中的涡脱落结构。
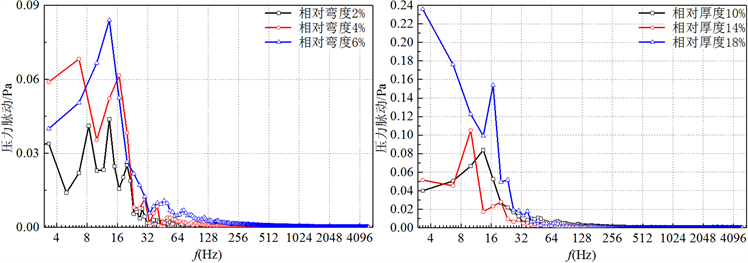(a) 厚度相同；弯度不同 (b) 弯度相同；厚度不同
Figure 9. Pressure fluctuation at trail edge of blade
图9. 叶片尾缘处压力脉动分布
声场中的测点布置如图10所示，距翼型中心半径为5C的环形一周内共设置24个测点(每隔15˚一点)，由于叶片与观察点之间的距离超过2C，故可认为是几何远场 [16]。
图11为5种叶片的声场计算结果，它们声学指向性分布均呈“8”字状，为典型偶极子源噪声。相对弯度从2%变化至4%时，叶片总声压级略有增加但变化不大，但从4%变化至6%时，叶片辐射噪声增加明显。随着相对厚度的增加，叶片声学指向性“8”字外扩，绕流产生的噪声也越大。故模型A因其弯度最小、厚度最薄而声学性能最优。
Figure 10. Far-field noise measurement point distribution
图10. 远场噪声测点
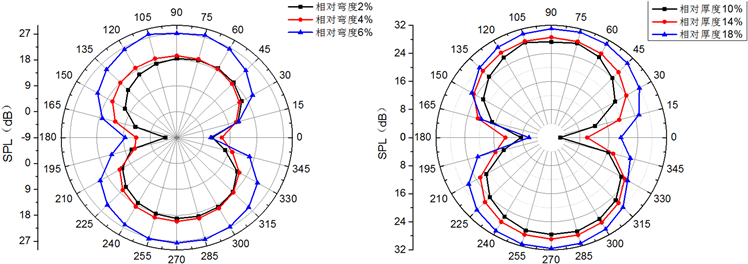(a) 厚度相同；弯度不同 (b) 弯度相同；厚度不同
Figure 11. Comparison of acoustic directivity of blade
图11. 叶片声学指向性分布
4. 结论
1) 叶片弯度增加使叶片吸力面低压区和压力面高压区范围增大且向尾缘延伸，上下翼面的压差扩大，叶片的气动性能得到改善；叶片厚度对叶片吸力面压力分布影响不大，但此参数增大会显著减小压力面的高压区分布，削弱叶片的气动性能。
2) 来流攻角小于12˚时，增加叶片弯度有利于增升，减小叶片厚度有利于增升减阻，这些方式均可提高叶片的升阻比。大攻角下，叶片几何参数对叶片气动性能的影响规律不如小攻角下明显。
3) 叶片厚度、弯度增大不仅会使叶片分离点位置前移，还会恶化分离后的边界层内流动，使边界层增厚、层内速度扰动加剧，不稳定流动与叶片间的相互作用增强。
4) 叶片绕流辐射噪声为典型偶极子源噪声特征，弯度越小、厚度越薄的叶片声学性能更优，但小弯度叶片气动性差，故综合考虑叶片气动及噪声特性时，叶片弯度这一参数需要折衷考量。