基于属性偏序结构图的关联规则提取方法

An Association Rule Extraction Method Based on Attribute Partial Order Structure Diagrams

摘要: 针对Apriori算法生成大量冗余关联规则的问题，本文提出了一种基于属性偏序结构图的关联规则提取方法。该方法旨在寻找相同支持度下的最大频繁项目集，进而提取无冗余关联规则。本文提出的方法不仅减少了挖掘频繁项目集的数量，从而提高关联规则提取的效率，而且将关联规则转换成属性偏序结构图中的知识表示形式，实现了频繁项分层的关联规则可视化展示。具有较强的可读性，有助于用户对关联规则进行深入分析，提高对潜在知识的利用和发掘程度。

Abstract: Aiming at the problem of Apriori algorithm generating a large number of redundant association rules, this paper proposes an association rule extraction method based on attribute partial order structure diagrams. It can extract non-redundant association rules by finding the maximum fre-quent item sets under the same support. The method proposed in this paper can reduce the num-ber of mining frequent item sets, so as to improve the efficiency of extracting association rules. Moreover, the association rules are converted into the knowledge representation in the attribute partial order structure diagrams, which realizes the visualization of the association rules of the fre-quent item hierarchy. With strong readability, it is helpful for users to conduct in-depth analysis of association rules and improve the utilization and exploitation of potential knowledge.

1. 引言

关联规则挖掘是数据挖掘研究中的一个重要部分，旨在挖掘数据库中有意义的关联。1993年由Agrawal等 [1] 提出的Apriori算法，是经典的挖掘布尔型频繁项目集的算法并得到广泛使用。利用Apriori算法获得的关联规则往往存在大量的冗余，而且对规则的可视化存在不足。关联分析与规则的可视化结合，有利于人们发现隐藏的知识，已经引起了许多学者的关注。概念格是一种从形式背景进行数据分析和规则提取的强有力工具，通过生成Hasse图能够直观表示出概念之间的层次关系，并且能够体现概念之间的泛化和例化关系 [2]。因此在形式概念分析理论下，基于概念格的关联规则提取的研究倍受学者关注 [3] [4]。目前，已有很多基于概念格的规则提取算法。胡可云 [5] 等提出一个从概念格上提取关联规则和分类规则的算法，实现了关联规则和分类规则的挖掘在概念格框架下的统一。王德兴等 [6] 利用量化概念格获取频繁项目集，方法直观，表示简洁。杨葛英等 [7] 提出了以概念格为背景的关联规则可视化方法，在概念格中展现关联规则路径。

形式概念分析强调的是属性与对象之间严谨的充要关系，与形式概念分析理论不同，关联规则注重的是属性间联系的紧密程度，而属性偏序结构图恰好提供了较为松散的属性关联研究视角。属性偏序结构图 [8] 是从形式概念分析理论发展而来的不同原理的知识发现数学方法，它从认知事物的角度出发，挖掘形式背景中对象之间、属性之间以及属性与对象之间的关系。属性偏序结构图中边与边之间不交叉，当形式背景中对象和属性增加时，概念格的复杂程度增大，可读性降低，而属性偏序结构图仍然层次关系明确，因此有助于更直观地进行知识模式发现和规则提取。目前属性偏序结构图在中医药数据挖掘、模式识别分类等相关研究中取得了很好的应用效果 [9] [10] [11]。本文主要研究无冗余关联规则提取方法和关联规则可视化表现形式，提出了一种基于属性偏序结构图的关联规则提取方法。将无冗余关联规则提取问题转化成挖掘数据集中相同支持度下的最大频繁项目集问题，并把频繁项转化成属性偏序结构图中的知识表示，为关联规则的提取提供了新的发现视角。理论分析证明，本文提出的方法是有效的。

2. 预备知识

定义1 [1] 称 $K=\left(U,A,I\right)$ 为一个形式背景，其中U为对象集，A为属性集，I为U和A之间的二元关系， $I\subseteq U\times A$。若 $x\in U,a\in A,\left(x,a\right)\in I$，则说x具有属性a，记为 $xIa$。

定义2 [1] 在形式背景 $K=\left(U,A,I\right)$ 中，对任意的 $G\subseteq U$， $B\subseteq A$，定义

$f(G)=\{a\in A|\forall x\in G,(x,a)\in I\}$

$g\left(B\right)=\left\{x\in U|\forall a\in B,\left(x,a\right)\in I\right\}$

$f\left(X\right)$ 表示G中所有对象共同拥有的属性组成的集合， $g\left(B\right)$ 表示B中所有属性的对象组成的集合。

定义3 [12] 在形式背景 $K=\left(U,A,I\right)$ 中，如果属性 $m\in A$ 满足

$g\left(m\right)=U$

则称属性m为形式背景K的最大共有属性。

定义4 [12] 在形式背景 $K=\left(U,A,I\right)$ 中，如果属性 $m_0,m_1,m_2,\cdots ,m_k\in A$ 满足

$g\left(m_t\right)\subseteq g\left(m_0\right),t=1,2,3,\cdots ,k,k\ge 2$

则称在形式背景K中，属性 $m_0$ 为属性集合 $\left\{m_1,m_2,\cdots ,m_k\right\}$ 的共有属性。

定义5 [12] 在形式背景 $K=\left(U,A,I\right)$ 中，如果属性 $m\in A$ 满足

$\left|g\left(m\right)\right|=1$

则称属性m为形式背景K的独有属性，其中 $\left|g\left(m\right)\right|$ 表示具有集合 $g\left(m\right)$ 的基数。

属性偏序结构图的构建步骤 [8]。

Step 1：计算最大共有属性 $M_0$ 及其结点 $C_0$，若不存在最大共有属性，则增加 $\left(\varnothing ,U\right)$ 作为顶层结点；

Step 2：在最大共有属性 $M_0$ 下计算所有共有属性集合 $\left\{m_{11},m_{12},\cdots ,m_{1p}\right\}$ 和独有属性集合 $\left\{s_{11},s_{12},\cdots ,s_{1p}\right\}$ 及其对应二元组 $\left\{C_{m1},C_{m2},\cdots ,C_{mp}\right\}$ 和 $\left\{C_{s1},C_{s2},\cdots ,C_{sp}\right\}$，并与最大共有属性的结点 $C_0$ 间绘制有向边。

如果该层有序对结点与最大共有属性的结点间满足关系：

${\displaystyle \underset{i=1}{\overset{p}{\cup }}g\left(m_{1i}\right)}\cup {\displaystyle \underset{i=1}{\overset{q}{\cup }}g\left(m_{1i}\right)}=U$,

则进入下一步；不满足上式时，在最底层结点与最大共有属性的结点间存在k条有向边。其中，

$k=\left|U-{\displaystyle \underset{i=1}{\overset{p}{\cup }}g\left(m_{1i}\right)}\cup {\displaystyle \underset{i=1}{\overset{q}{\cup }}g\left(m_{1i}\right)}\right|$。

Step 3：在上层每个共有属性结点 $\left\{C_{m1},C_{m2},\cdots ,C_{mp}\right\}$ 下，计算上层共有属性 $m_{ti}$， $t\in \left(1:p\right)$ (t表示上一层的层数)的共有属性 $\left\{m_{t+1,1},m_{t+1,2},\cdots ,m_{t+1,l}\right\}$ 和独有属性 $\left\{s_{t+1,1},s_{t+1,2},\cdots ,s_{t+1,k}\right\}$ 及其对应二元组结点 $\left\{C_{t+1,1},C_{t+1,2},\cdots ,C_{t+1,l}\right\}$ 和 $\left\{C_{st+1,1},C_{st+1,2},\cdots ,C_{st+1,k}\right\}$，在每个独有属性的二元组结点 $\left\{C_{s1},C_{s2},\cdots ,C_{sq}\right\}$ 下计算独有属性 $\left\{s{c}_{t+1,1},s{c}_{t+1,2},\cdots ,s{c}_{t+1,q}\right\}$ 及其二元组结点 $\left\{C{s}_{t+1},C{s}_{t+2},\cdots ,C{s}_{t+q}\right\}$。

如果上层结点 $\left\{C_{m1},C_{m2},\cdots ,C_{mp}\right\}$ 与其共有属性结点 $\left\{m_{t+1,1},m_{t+1,2},\cdots ,m_{t+1,l}\right\}$ 和独有属性结点 $\left\{C_{s1},C_{s2},\cdots ,C_{sk}\right\}$ 间满足关系：

${\displaystyle \underset{i=1}{\overset{p}{\cup }}g\left(m_{t+1,i}\right)}\cup {\displaystyle \underset{i=1}{\overset{q}{\cup }}g\left(s_{t+1,i}\right)}=g\left(m_j\right),j\in \left(1:p\right)$

则进入下一步；不满足时，在最底层结点与相应共有属性的结点间绘制l条有向边，

$l=\left|g\left(m_j\right)-{\displaystyle \underset{i=1}{\overset{p}{\cup }}g\left(m_{t+1,i}\right)}\cup {\displaystyle \underset{i=1}{\overset{q}{\cup }}g\left(s_{t+1,i}\right)}\right|,j\in \left(1:p\right)$

Step 4：当在共有属性或独有属性下不能生成新的二元结点时停止，否则调至Step 3。

Step 5：算法结束。

3. 属性偏序结构图中的关联结点和关联路径

本节将在属性偏序结构图中给出关联规则的关联结点，关联路径的相关定义及关联规则支持度和置信度的计算。

定义6在属性偏序结构图 $\Re \left(U,A,I\right)$ 中，若结点 $\left(A^{\prime },U^{\prime }\right)$ 蕴涵关联规则 $X\Rightarrow Y$，即 $X\subset A^{\prime },Y\subset A^{\prime }$，则称结点 $\left(A^{\prime },U^{\prime }\right)$ 为关联规则 $X\Rightarrow Y$ 的关联结点。由结点 $\left(A^{\prime },U^{\prime }\right)$ 向底层结点 $\left(A,\varnothing \right)$ 建立的边称作关联规则 $X\Rightarrow Y$ 的关联路径。

定义7对于关联规则 $X\Rightarrow Y$，在属性偏序结构图 $\Re \left(U,A,I\right)$ 中的所有关联结点的集合记为 $C_{\left(X\Rightarrow Y\right)}=\left\{\left(A_1,U_1\right),\left(A_2,U_2\right),\cdots ,\left(A_k,U_k\right)|k\in N^{+}\right\}$，定义关联规则 $X\Rightarrow Y$ 的支持度为

$support\left(X\Rightarrow Y\right)=\frac{\left|U_1\cup U_2\cup \cdots \cup U_k\right|}{\left|U\right|}$

其中， $\left|•\right|$ 表示基数。

定义8在属性偏序结构图 $\Re \left(U,A,I\right)$ 中，所有包含属性集(项目集) B的结点记为 $C_{\left(B\right)}=\left\{\left(B_1,U_{B1}\right),\left(B_2,U_{B2}\right),\cdots ,\left(B_n,U_{Bn}\right)|n\in N^{+}\right\}$，定义B的支持度为

$support\left(B\right)=\frac{\left|U_{B1}\cup U_{B2}\cup \cdots \cup U_{Bn}\right|}{\left|U\right|}$

如果 $support\left(B\right)$ 大于支持度阈值 $\min \underset{\_}{}sup$，则称B为频繁项目集。如果B包含k个属性，则称B为频繁k-项集。

定义9若在属性偏序结构图 $\Re \left(U,A,I\right)$ 中存在关联规则 $X\Rightarrow Y$，则其置信度为

$confidence\left(X\Rightarrow Y\right)=\frac{support\left(X\cup Y\right)}{support(\; X\; )}$

给定最小置信度 $\min \underset{\_}{}conf$，如果规则 $X\Rightarrow Y$ 同时满足最小支持度 $\min \underset{\_}{}sup$ 和最小置信度 $\min \underset{\_}{}conf$，则称该规则为强关联规则。

定义10对于属性集(项目集) $W\subset X\subseteq A$，如果 $support\left(W\right)=support\left(X\right)\ge \min \underset{\_}{}sup$，并且对于任何的 $Z\supset X$，均有 $support\left(Z\right)<support\left(X\right)$，则称X为W在相同支持度下的最大频繁项目集。

定理1对于规则 $X\Rightarrow Y$， $W\Rightarrow Y$，满足 $W\subset X$ 且 $support\left(W\right)=support\left(X\right)$，则 $W\Rightarrow Y$ 是 $X\Rightarrow Y$ 的冗余规则。

证明：因为 $support\left(W\Rightarrow Y\right)=support\left(W\cup Y\right)$， $support\left(X\Rightarrow Y\right)=support\left(X\cup Y\right)$ 且 $W\subset X$，所以 $support\left(W\cup Y\right)\ge support\left(X\cup Y\right)$，即 $support\left(W\Rightarrow Y\right)\ge support\left(X\Rightarrow Y\right)$。因此 $\frac{support\left(W\Rightarrow Y\right)}{support\left(W\right)}\ge \frac{support\left(X\Rightarrow Y\right)}{support\left(X\right)}$，即 $confidence\left(W\Rightarrow Y\right)\ge confidence\left(X\Rightarrow Y\right)$。若 $X\Rightarrow Y$ 满足支持度阈值 $\min \underset{\_}{}sup$ 和最小置信度 $\min \underset{\_}{}conf$， $W\Rightarrow Y$ 也必定满足条件。

定理2对于规则 $Y\Rightarrow X$， $Y\Rightarrow W$，满足 $W\subset X$ 且 $support\left(W\right)=support\left(X\right)$，则 $Y\Rightarrow W$ 是 $Y\Rightarrow X$ 的冗余规则。

证明：因为 $support\left(Y\Rightarrow W\right)=support\left(Y\cup W\right)$， $support\left(Y\Rightarrow X\right)=support\left(Y\cup X\right)$ 且 $W\subset X$，所以 $support\left(Y\cup W\right)\ge support\left(Y\cup X\right)$，即 $support\left(Y\Rightarrow W\right)\ge support\left(Y\Rightarrow X\right)$。因此 $\frac{support\left(Y\Rightarrow X\right)}{support\left(Y\right)}\ge \frac{support\left(Y\Rightarrow W\right)}{support\left(Y\right)}$，即 $confidence\left(Y\Rightarrow W\right)\ge confidence\left(Y\Rightarrow X\right)$。若 $Y\Rightarrow X$ 满足支持度阈值 $\min \underset{\_}{}sup$ 和最小置信度 $\min \underset{\_}{}conf$， $Y\Rightarrow W$ 也必定满足条件。

由定理1和定理2可知，从数据集中挖掘相同支持度下的最大频繁项目集进行关联规则提取即可获得无冗余关联规则。

4. 基于属性偏序结构图提取关联规则的原理及方法

在Apriori算法中，频繁项的提取是关联规则提取的关键步骤，Apriori算法的总体性能主要由这一步决定。而由数据集产生的频繁项集数目往往会非常大，导致挖掘过程比较繁琐，生成大量冗余规则。本节提出基于属性偏序结构图的关联规则提取方法，从属性偏序结构图中寻找相同支持度下的最大频繁项目集，减少频繁项目集数量，提高关联规则挖掘效率，并获得无冗余的关联规则。下面从构图原理和数学角度说明从属性偏序结构图中提取频繁项的合理性和科学性。

根据属性偏序结构图的构图步骤step 2，计算最大共有属性 $M_0$ 下所有共有属性集合 $\left\{m_{11},m_{12},\cdots ,m_{1p}\right\}$ 和独有属性集合 $\left\{s_{11},s_{12},\cdots ,s_{1q}\right\}$ 及其对应二元组 $\left\{C_{m1},C_{m2},\cdots ,C_{mp}\right\}$ 和 $\left\{C_{s1},C_{s2},\cdots ,C_{sq}\right\}$，并与最大共有属性的结点 $C_0$ 间绘制有向边，说明属性偏序结构图是以属性覆盖对象的程度为偏序进行构图，所以相同支持度下的最大频繁项目集必定含于属性偏序结构图的结点中。如果该层有序对结点与最大共有属性的结点

间满足关系 ${\displaystyle \underset{i=1}{\overset{p}{\cup }}g\left(m_{1i}\right)}\cup {\displaystyle \underset{i=1}{\overset{q}{\cup }}g\left(m_{1i}\right)}=U$，则进入下一步。这保证了覆盖对象的全面性。也就是说形式背景

相同支持度下的最大频繁项目集必定包含属性集 $\left\{m_{11},m_{12},\cdots ,m_{1p}\right\}$ 或 $\left\{s_{11},s_{12},\cdots ,s_{1p}\right\}$ 中的元素。属性偏序结构图体现的是自下而上的属性聚合模式，所以可以从上到下扫描属性偏序结构图提取频繁项，即可得到相同支持度下的最大频繁项目集，进而提取无冗余的关联规则。

本文提出的基于属性偏序结构图的关联规则提取按照以下步骤进行。

Step 1：设置最小支持度 $\min \underset{\_}{}sup$，对形式背景进行第一遍扫描，生成频繁1-项集；

Step 2：由形式背景生成对应的属性偏序结构图，记最大共有属性 $M_0$ 下所有共有属性集合和独有属性集合分别为 $\left\{m_{11},m_{12},\cdots ,m_{1p}\right\}$ 和 $\left\{s_{11},s_{12},\cdots ,s_{1q}\right\}$ ；

Step 3：在属性偏序结构图中由上到下依次寻找包含 $\left\{m_{11},m_{12},\cdots ,m_{1p}\right\}$ 或 $\left\{s_{11},s_{12},\cdots ,s_{1q}\right\}$ 的频繁项集并提取对象支持集；

Step 4：设置最小支持度 $\min \underset{\_}{}conf$，依据挖掘的频繁项目集提取强关联规则并计算相应的置信度。

5. 例子说明

例1．表1给出了一个形式背景 $\left(U,A,I\right)$，对象集(事物集) $U=\left\{1,2,3,4,5,6\right\}$，属性集 $A=\left\{a,b,c,d,e,f,g\right\}$。它们之间的二元关系I如表1所示。表中的1表示对象具有某属性，0表示对象不具有某属性。利用本文所提方法进行关联规则提取步骤如下。

Step 1：设最小支持度 $\min \underset{\_}{}sup=2/7$，对形式背景进行第一遍扫描，得到频繁1-项集，见表2。

Step 2：由表1给出的形式背景生成对应的属性偏序结构图 $\Re$，如图1所示。

Step 3：提取属性偏序结构图中的频繁项。由图1可知结点(a, 1234)，(c, 6)和(d, 5)位于属性偏序结构

Table 1. A formal context ( U , A , I )

表1. 形式背景 $\left(U,A,I\right)$

Table 2. Frequent 1-items

表2. 频繁1-项集

Figure 1. APOSD $\Re$

图1. 属性偏序结构图 $\Re$

$\Re$ 的第二层，对应的属性分别为a，c，d。在图1中逐层向下搜索寻找相同支持度下的最大频繁项集，得到相同支持度下的最大频繁项集及其支持度如图2所示。

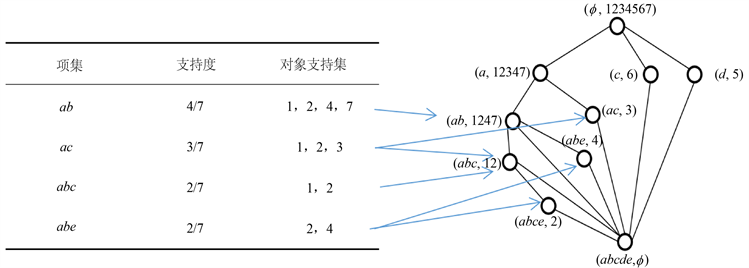
Figure 2. The frequent items are extracted from the APOSD

图2. 从属性偏序结构图中提取的频繁项集

Step 4：设 $\min \underset{\_}{}conf=80\%$，结合表1表2的频繁项集进行关联规则提取，得到关联规则，并计算其置信度如下：

$b\Rightarrow a$， $confidence\left(b\Rightarrow a\right)=\frac{support\left(ab\right)}{support\left(b\right)}=100\text{\%}$ ；

$a\Rightarrow b$， $confidence\left(a\Rightarrow b\right)=\frac{support\left(ab\right)}{support\left(a\right)}=80\text{\%}$ ；

$bc\Rightarrow a$， $confidence\left(b\text{c}\Rightarrow a\right)=\frac{support\left(abc\right)}{support\left(bc\right)}=100\text{\%}$ ；

$e\Rightarrow ab$， $confidence\left(e\Rightarrow ab\right)=\frac{support\left(abe\right)}{support\left(e\right)}=100\text{\%}$。

6. 结果对比分析

关联规则挖掘方法中，最典型的关联规则提取方法是Apriori算法。它是一种逐层搜索的迭代方法。扫描数据库直接得到频繁1-项集，在得到频繁1-项集的基础上寻找频繁2-项集。如此循环，在得到k-项集的基础上得到(k + 1)-项集，直到无法找出高频项集，停止迭代。根据频繁项集，导出所有的关联规则。

在设置同样的最小支持度 $\min \underset{\_}{}sup$ 和最小置信度 $\min \underset{\_}{}conf$ 时，利用传统的Apriori算法产生的频繁项集及支持度如表3所示。

根据表3中的频繁项集，提取出的关联规则及置信度如表4所示。

对比可知，Apriori算法得到频繁项目集为11个，在属性偏序结构图中利用本文提出的方法得到的频繁项目集为9个。频繁项目集个数缩减了2个，在一定程度上起到了减少提取关联规则计算时间的作用。基于属性偏序结构图的关联规则提取方法获得的关联规则为 $b\Rightarrow a$， $a\Rightarrow b$， $bc\Rightarrow a$， $e\Rightarrow ab$。与Apriori算法比较减少2个关联规则 $e\Rightarrow a$， $e\Rightarrow b$。而关联规则 $e\Rightarrow a$， $e\Rightarrow b$ 是所获得的关联规则 $e\Rightarrow ab$ 的冗余规则，可根据定理2证明。

Apriori算法的不足之处在于，每次寻求频繁k-项集都需要扫描一次数据库，需要对数据库进行反复扫描，占用了大量的时间和空间，并且生成大量的冗余规则。本文提出的方法通过对属性偏序结构图的频繁模式的遍历操作，代替了Apriori算法中对形式背景的多次扫描。在提取的频繁项目集的过程中，

Table 3. Frequent items and support degrees are based on Apriori algorithm

表3. Apriori算法产生的频繁项集及支持度

Table 4. Association rules and confidence are based on Apriori algorithm

表4. Apriori算法产生的关联规则及置信度

获得的频繁项目集是相同支持度下的最大频繁项目集，从而在属性偏序结构图中寻找频繁项目集比Apriori算法挖掘频繁项目集个数有所缩减，同时更具有代表性，在已有的频繁项目集下生成的关联规则是无冗余的关联规则。除此之外，本文提出的基于属性偏序结构图的关联规则提取方法，使关联关系通过属性偏序结构图的结点的泛化与特化关系直观地体现出来，可读性比较强。如关联规则 $b\Rightarrow a$，对应于属性偏序结构图中的关联结点为 $\left(ab,1247\right)$， $\left(abc,12\right)$， $\left(abce,2\right)$， $\left(abe,4\right)$，标记出对应关联结点和关联路径，有助于用户理解所提取的关联规则，便于对关联规则进行深入分析。

7. 总结

本文首先证明了提取相同支持度下的最大频繁项目集即可得到无冗余关联规则。在分析属性偏序结构图的构图原理的基础上，从数学角度说明在属性偏序结构图中提取相同支持度下的最大频繁项目集的合理性和科学性，进而提出了基于属性偏序结构图的关联规则提取方法，获得无冗余的关联规则，实现频繁项分层的关联规则可视化展示。结合对象和属性两个角度从全局的知识背景中去分析关联关系，提高了对潜在知识和非关联关系的利用和发掘程度。将关联规则转换成属性偏序结构图中的知识表示形式，具有较强的可读性，有助于用户对关联规则进行深入分析和研究。

NOTES

^*通讯作者。