摘要:
本文考察了一阶非线性常微分边值问题
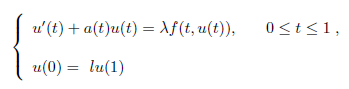
正解的存在性,其中f:[0,1]×[0,∞)→[0,∞),a:[0,1]→[0,∞)均为连续函数, 且∫
01a(θ)dθ > 0,λ为正参数,l为常数且0 < l < e
∫01a(θ)dθ.在非线性项 f 满足超线性, 欠线性和渐近线性的条件下,本文运用不动点指数理论获得了该问题正解的存在性。
Abstract:
In this paper, we consider the existence of positive solutions for the nonlinear first- order ordinary boundary value problems
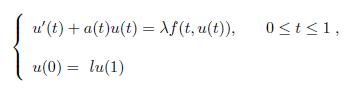
where f:[0,1]×[0,∞)→[0,∞),a:[0,1]→[0,∞) are continuous functions and ∫
01a(θ)dθ > 0, λ is a positive parameter, l is a constant, and 0 < l < e
∫01a(θ)dθ . Under the assumption that the nonlinear term f satisfies superlinear, sublinear and asymptotic growth conditon, the existence of positive solutions of the problem is obtained by using the fixed-point index theory.