基于自优化模拟技术的梯级水电站耗能最小模型

Minimum Energy Consumption Model of Cascade Hydropower Stations Based on Self-Optimization Simulation Technology

摘要: 针对水库优化调度模型求解方法中，传统动态规划(DP)法存在“维数灾”，求解耗时较长等不足，提出基于自优化模拟技术的水电站水库调度模型快速求解方法(SOST)。该方法在满足水电站负荷要求和最小下泄流量要求的前提下，尽可能提高水库调度期的运行水位以寻求全局优化调度解。选取潘口–小漩梯级水电站30个典型日的历史运行数据作为计算实例，汛期典型日的小时尺度优化调度结果显示：该方法能够实现潘口–小漩梯级水电站总负荷的经济分配，优化分配计算所得梯级水电站总耗能为104.23万kW•h，比实际运行耗能减少3.89%。相较于传统的DP算法，该方法计算时间降幅达58.04%。SOST法寻优性能较好，可有效提高水能利用效率，为梯级水电站发电优化调度提供参考。

Abstract: The traditional dynamic programming (DP) method has the disadvantages of “dimension disaster” and long solving time. According to the characteristics of low water consumption rate of reservoir in high head operation, a fast solution method for reservoir operation model of hydropower station based on self-optimization simulation technology (SOST) is proposed. Under the premise of meeting the load requirements and minimum discharge requirements of hydropower station, the method can improve the operation level of reservoir as much as possible to seek the global optimal operation solution. Taking the historical operation data of 30 typical days of Pankou-Xiaoxuan cascade hydropower sta-tions as an example, the hourly optimal operation results of typical days in flood season show that this method can realize the economic distribution of total load of Pankou-Xiaoxuan cascade hydropower stations, and the total energy consumption of the cascade hydropower stations calculated by the op-timal distribution is 1,042,300 kW•h, which is 3.89% less than the actual operation energy consump-tion. Compared with the traditional DP algorithm, the calculation time of this method is reduced by 58.04%. The results show that the SOST method has good performance and can effectively improve the utilization efficiency of water energy, which provides a reference for the optimal operation of cascade hydropower stations.

1. 引言

梯级水电站短期优化调度(梯级调度)的目标是在满足多种约束条件下，寻求最大发电效益。为实现这一目标，梯级水电站可以采用不同的模型进行优化调度，如耗水量最小模型、耗能最小模型等 [1] [2]。耗水量最小模型虽然能够有效减少发电耗水，节约水资源，增加水库调度期末的蓄水量，但是由于其仅注重发电的耗水量，没有关注水体的水头效应，因而，在从单个水库推广至梯级时，应用受到限制 [3] [4]；作为另一种常用调度模型，耗能最小模型，概念简单直观，其从能量角度对水量所具有的能量进行刻画，对于发电效益的描述更为准确 [5] [6]，因此，针对所求解的梯级水电站短期优化调度问题，本文构建耗能最小模型并进行求解。

梯级水电站短期优化调度属于非线性规划问题，维数多且约束复杂。针对该问题，多种优化算法被提出。主要分为传统优化算法和智能优化算法，前者的特点是结构较为固定，可以获得较为可靠的结果，但计算耗时较长，不适用于对实时性要求较高的场景，并且随着计算维度的增加会出现“维数灾”问题。后者的特点是计算耗时较短，求解效率较高，且能有效缓解“维数灾”问题，但其收敛性存在不确定性，无法保证每次计算都能收敛到全局最优，因而具有一定的随机性。

自优化模拟技术是一种有效的模型求解方法，由雷声隆 [7] 等利用现代控制论基本原理，在南水北调东线工程规划中提出。该方法在常规模拟技术基础上增加了在线辨识与反馈机理，使得拟解决的问题不仅可以沿其总体优良的决策方向寻优，而且可以控制系统的运转过程。1995年，邵东国、郭元裕等从数值计算分析上对自优化模拟技术进行了实例验证，1997年，沈佩君等从理论上证明了自优化模拟技术的收敛性 [8]；灵活利用调蓄工程(水库)具有最优决策域的特点，应用中以顺时序模拟得到的防破坏蓄水线和逆时序模拟得到的经济蓄水线包裹的区域作为最优决策域。2002年，罗强等针对水库调度的特点，从理论上证明了单一水库调度自优化模拟技术最优决策域的存在性，即证明了由顺时序模拟得到的防破坏蓄水线和逆时序模拟得到的经济蓄水线形成了一个封闭的区域，并对这一区域是否为最优决策域进行了证明 [9]。

自优化模拟技术具有较好的仿真性，并且算法收敛速度快，在进行多库联合优化调度时，其计算时间仅随水电站数量线性增加，可有效缓解“维数灾”问题，计算效率高。因此，为保证梯级水电站优化调度结果的收敛性和最优性，将自优化模拟技术引入到梯级水电站短期优化调度问题的求解中，以期充分发挥梯级的补偿调节作用，实现总负荷在各水电站间的优化分配，促进水能资源的高效利用。

2. 研究对象概况

堵河位于湖北省西北部，是汉江支流，全长354 km，流域面积12,502 km²，多年平均流量236 m³/s。潘口水电站水库位于堵河干流上游河段，多年平均流量164 m³/s，多年平均年径流量51.7亿m³ [10]。小漩水电站水库距上游潘口水电站水库约10.4 km，小漩水电站具备日调节能力。

3. 模型建立及求解

3.1. 梯级耗能最小模型建立

建立以时段梯级耗能最小为目标的优化调度模型，从水电能源相互转换的角度出发，建立优化调度模型如下：

1) 目标函数：

$E={\displaystyle \underset{i=1}{\overset{M}{\sum }}{\displaystyle \underset{t=1}{\overset{T}{\sum }}9.81}\cdot H_{i,t}\cdot Q_{i,t}\cdot \Delta t}$ (1)

式中，E为时段梯级耗能， $H_{i,t}$ 为第i个水电站t时段的平均水头， $Q_{i,t}$ 为第i个水电站t时段的发电流量， $\Delta t$ 为时段长度，M为梯级中水电站的个数，T为调度期总时段数。

2) 约束条件：

水量平衡约束：

$V_{i,t}=V_{i,t-1}+\left(I_{i,t}-Q_{i,t}\right)\cdot \Delta t$ (2)

式中， $V_{i,t}$ 为第i个水电站t时段末的蓄水量， $I_{i,t}$ 为第i个水电站t时段的入库流量。

梯级总负荷平衡约束：

$N_t=N_{1,t}+\cdots +N_{i,t}+\cdots +N_{M,t}$ (3)

式中， $N_t$ 为t时段梯级总出力， $N_{i,t}$ 为第i个水电站t时段出力。

水头约束：

$H_t^{\min }\le H_t\le H_t^{\max }$ (4)

式中， $H_t$ 为水电站水头， $H_t^{\min }$ 为维持水电站稳定运行的最小水头， $H_t^{\max }$ 为维持水电站稳定运行的最大水头。

水位约束：

$Z_t^{\min }\le Z_t\le Z_t^{\max }$ (5)

式中， $Z_t$ 为水电站运行水头， $Z_t^{\min }$ 和 $Z_t^{\max }$ 为t时段水电站水位约束。

下泄流量约束：

$Q_t^{\min }\le Q_t\le Q_t^{\max }$ (6)

式中， $Q_t^{\min }$ 和 $Q_t^{\max }$ 为t时段水电站下泄流量约束。

3.2. 模型求解流程

自优化模拟技术是在自适应控制原理的基础上，将一般模拟技术的输出结果反馈至输入端，从而将梯级水电站群的输入参数进行改变，进行多次的模拟试验引导，最终使得模拟结果趋于目标值的最优，自动生成梯级水电站群的最优运行策略。其具体步骤如下：

步骤1：输入各个水电站水库的状态初值，包括水电站日发电量计划值以及水电站历史运行数据，确定调度模型参数并赋给初始值。

步骤2：建立优化调度模型，将过去若干年分为连续的短期调度期，依次对各调度期进行优化调度计算。

步骤3：顺流向模拟。顺时序模拟依次进行厂内优化计算，确定各水电站的初始运行过程线。在满足下游河道水电站生态需水的前提下，进行梯级水电站时段负荷分配并维持高水位运行。接着进行逆时序模拟，若顺时序时段末水位处于限制水位范围之外，那么需要以前一时段末的水位作为时段初水位，重新计算该时段的水电站出力。

步骤4：各个水电站进行运行模拟决策过程。进行负荷分配，计算时段初、末的发电流量。将厂内所有发电机组按从小到大编号，对于第j阶段，以机组的编号j为阶段变量，以第j台发电机组的负荷 $N_j$ 为决策变量，以1~j台发电机组的累积负荷 $N_j^{all}$ 为状态变量。分别按式(7)和式(8)确定状态转移方程和当前阶段决策，接着进行逆推计算，得到各发电机组的最优分配发电流量和最优分配负荷。

$N_j^{all}=N_{j-1}^{all}+N_j$ (7)

$\{\begin{array}{l}{Q}_j^{all*}\left(N_j^{all}\right)=\min \left[Q_j\left(N_j\right)+Q_{j-1}^{all*}\left(N_{j-1}^{all}\right)\right]\\ Q_0^{all*}\left(N_0^{all}\right)=0\end{array}$ (8)

其中： $Q_j^{all*}$ 是j阶段最优总分配发电流量， $Q_j$ 是第j台发电机组的发电流量， $Q_0^{all*}$ 和 $N_0^{all}$ 分别是开始阶段的发电流量和分配负荷。

步骤5：当顺流向模拟完成后，将顺流向协调耦合所得各水电站的下泄水量过程 $DL\left(t\right)$ 作为反馈修正量，用于后续的决策控制。进行逆流向模拟，将各水电站的入库流量，再加上反馈到输入端的反馈修正量，成为各个水电站新的入库流量。并收紧全部约束条件，即调控水电站的入库流量需要受到下游水电站运行出库流量的限制，建立新的模拟控制线。

步骤6：判断控制线是否收敛于最优控制线，目标值的收敛程度是否在给定的范围之内，若都满足则整理运行结果，得出结论。若不满足则返回步骤3进行下一轮的模拟迭代过程。具体流程见图1。

4. 实例计算

基于上述模型，以潘口、小漩单个水电站和潘口–小漩梯级水电站为例，选取30个典型日的历史运行数据作为计算实例，其中汛期典型日的小时尺度优化调度结果如下所示。

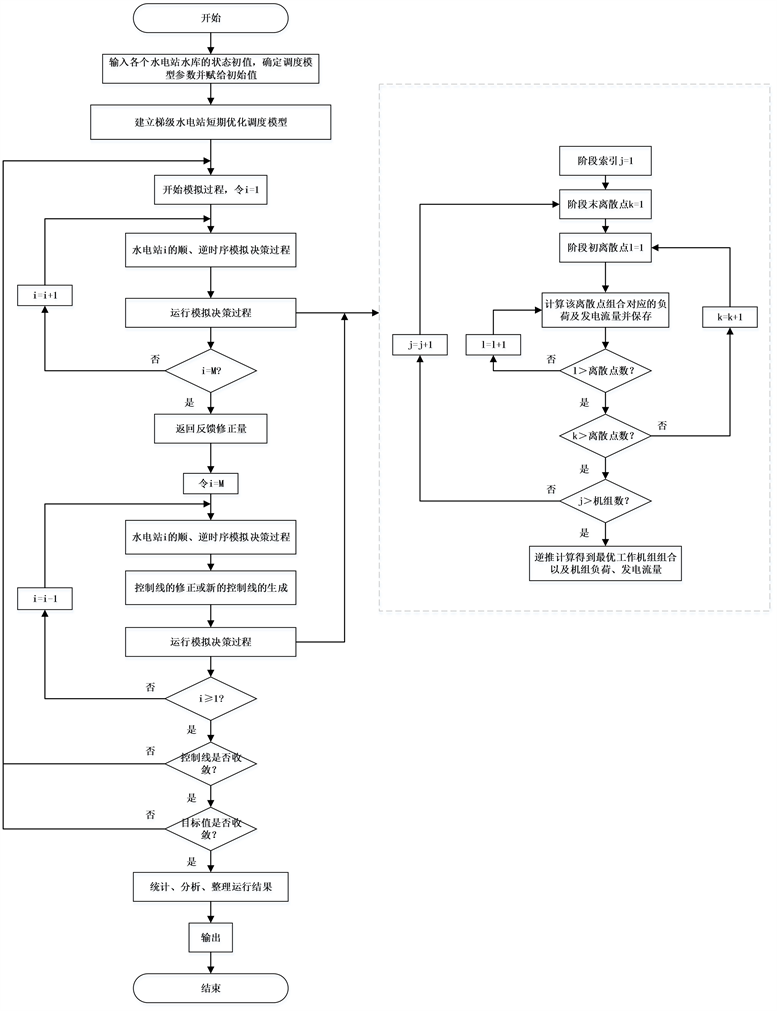
Figure 1. Flow chart of solving cascade energy consumption minimum model based on self optimization simulation technology

图1. 基于自优化模拟技术的梯级耗能最小模型求解流程图

Table 1. Output and water level of Pankou hydropower station on typical days in flood season

表1. 汛期典型日的潘口水电站出力和水位

Figure 2. Change process of output and water level of Pankou hydropower station

图2. 潘口水电站出力和水位变化过程

由表1和图2可得，对潘口水电站进行分析，0~7时潘口水电站停机，没有出力，7时后开机，库水位缓慢下降。经过梯级耗能最小模型对计算水位进行优化，8~19时保持65 MW左右的出力，20时出力加大到140 MW左右。计算水位与实际水位基本重合，说明优化过程对于潘口水电站调度无太大影响，耗能减少的部分主要在于小漩水电站。

Table 2. Output and water level of Xiaoxuan hydropower station on typical days in flood season

表2. 汛期典型日的小漩水电站出力和水位

由表2和图3可知，对小漩水电站进行分析，0~7时维持2 MW左右的基本出力，此时水位从263.6 m下降到263.4 m左右，实际水位和计算水位的趋势基本保持一致。8~23时的出力加大到16 MW左右，在20时和21时两个时间点达到最大，为24 MW左右，计算水位与实际水位曲线变化较大，且基本位于实际水位上方。同时实际水位曲线趋势基本为下降趋势，而计算水位曲线趋势却呈上升趋势，优化调度方案中小漩运行水位明显高于实际，保持高水位运行使得小漩在发电水量相同的情况下可以发出更多的电量。

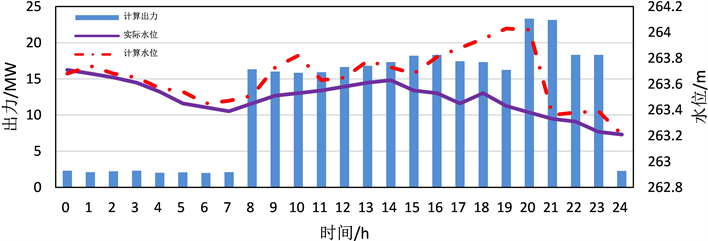
Figure 3. Change process of output and water level of Xiaoxuan hydropower station

图3. 小漩水电站出力和水位变化过程

Table 3. Water level and energy consumption of Pankou, Xiaoxuan and Pankou-Xiaoxuan cascade hydropower stations

表3. 潘口、小漩以及潘口–小漩梯级水电站的水位和耗能

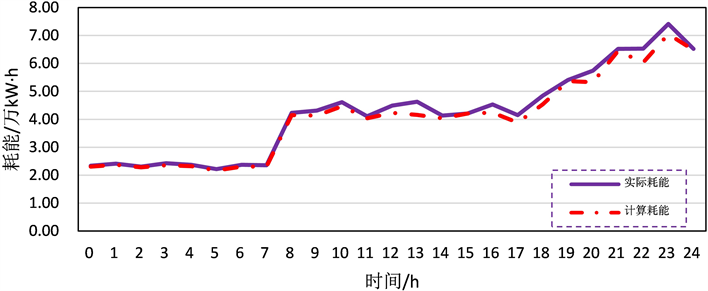
Figure 4. Energy consumption change process of Pankou-Xiaoxuan cascade hydropower station

图4. 潘口–小漩梯级水电站耗能变化过程

由表3和图4可得，经过优化模拟后，计算耗能相比实际耗能确实有一定的降低0~7时电站出力较低时，实际耗能与计算耗能基本保持一致，并无太大区别。9时后出力加大，实际耗能和计算耗能出现差别，说明耗能优化主要集中在一天中出力较大的时段，这与图3和图4所显示的规律相吻合。

对潘口–小漩梯级水电站整体进行分析，如下表4所示，计算过程中，优化分配后的梯级负荷曲线与实际运行曲线十分接近，最大负荷绝对偏差为3.43 MW，最大负荷相对偏差为0.24%，平均负荷偏差为0.08 MW，平均负荷相对偏差为0.01%，时段负荷平衡约束基本满足。各站优化分配计算发电量与实际发电量偏差均在0.1%以内，梯级总发电量比实际少0.01%，电量平衡约束亦基本满足。

潘口–小漩梯级水电站实际运行总耗能为108.21万kW·h，优化调度后运行总耗能为104.23万kW·h，耗能减少3.89%。原因在于潘口水电站是高水头水电站，而小漩水电站是低水头电站。因此虽然小漩水电站的运行水位抬升对潘口确实存在影响，但这对于高水头水电站的影响比较有限；相比之下，小漩水电站机组对于水头变化的敏感程度更高，因此耗能的减少程度更加明显。

Table 4. Power generation deviation and energy consumption difference of Pankou, Xiaoxuan and cascade hydropower stations

表4. 潘口、小漩以及潘口–小漩梯级水电站发电量偏差和耗能差

分别采用自优化模拟技术(SOST)、动态规划法(DP)，对潘口–小漩梯级水电站进行仿真模拟计算，两种方法各运行15次，计算结果如表5所示。

Table 5. Calculation results of energy consumption of Pankou-Xiaoxuan cascade

表5. 潘口–小漩梯级耗能计算结果

由表5计算结果可以看出：自优化模拟技术的耗能相对于动态规划法仅增加了0.12万kW·h，增幅仅为0.01%，说明自优化模拟技术有着较好的寻优性能。同时计算时间降幅58.04%，说明自优化模拟技术可以大幅减少求解计算耗时，提高计算效率。

5. 结论

针对水库优化调度模型求解方法中，传统动态规划(DP)法存在“维数灾”，求解耗时较长等不足。本文将自优化模拟技术引入到潘口–小漩梯级水电站短期优化调度问题求解中，提出了基于自优化模拟技术的水电站水库调度模型快速求解方法(SOST)。选取潘口–小漩梯级水电站30个典型日的历史运行数据作为计算实例，汛期典型日的小时尺度优化调度结果显示：该方法能够降低潘口–小漩梯级水电站运行耗能，并且在极大程度上提高求解效率，可为梯级水电站发电优化调度提供参考。

基金项目

国家自然科学基金(51709105)；中央高校项目基金(2020MS026，2019MS031)，中国博士后科学基金 (2020M680487)。