1. 引言
我国水能资源蕴藏丰富 [1],理论上蕴藏量超过1万kW的河流超过3000条,装机容量可达5.4亿kW,年发电量可达6.1万亿kW∙h。技术可开发年发电量达到2.5万亿kW∙h。理论蕴藏量占全球理论蕴藏15%,技术可开发量占全球17% [2]。我国水能资源富集主要集中在大江大河干流,有助于流域梯级滚动开发,规模效益显著 [3]。目前我国形成的“十三大水电基地”,技术可开发量占全国总量51.4%。经过多年“流域开发”,我国西北、西南地区逐步形成了特大流域和干流的梯级水电站群 [4]。已建好的梯级水电站群投产并网后,如何大范围优化水资源配置,发挥出最大经济效益,成为当前亟需解决的问题。
传统的优化算法一般以运筹学和最优理论为基础,较常用方法有:Lagrange松弛法 [5]、线性规划 [6]、非线性规划 [7]、混合整数规划 [8]、动态规划算法 [9] [10] 等。其中动态规划算法能分阶段逐步优化,无需初始解,求解非线性、非凸问题可收敛至最优解,广泛应用于梯级水电站优化调度。但梯级水电站优化调度模型具有多阶段性、时滞性、非线性的特点,且随着电站数目的增加,为了获得更高精度的解而增加时段状态的离散数,会使计算时间层呈“指数”增加,“维数灾”的问题十分严峻 [11]。
随着计算机技术的发展,为了应对“维数灾”,提高算法求解效率,部分学者采用遗传算法对梯级水电站进行优化求解 [12] [13]。遗传算法模拟大自然中的生物进化规律和遗传学机理而提出的一种计算模型。通过模拟自然进化过程而寻求最优解方法。将待求解的数学问题转化为生物进化中的染色体基因的交叉、变异等过程,最终求得最优解。遗传算法在求解梯级水电站优化调度中取得了较好的结果。然而遗传算法易受初始解的影响,很容易陷入局部最优,为此本文提出了一种改进策略,对遗传算法进行改进,与改进前相比,改进后求解效率更高。
2. 求解方法与策略
2.1. 目标函数与约束条件
以梯级发电量最大为目标函数:
(1)
式中T表示调度时段个数,
表示电站m的综合出力系数,
为电站m在t时刻的发电流量,
为电站m在t时刻的水头。
水力约束:
一般来说,梯级水电站具有很强的水力联系,其上游出库流量,直接影响到下游入库,因此在考虑其水力约束时应当考虑其上下游水力联系,此外还应当满足上下游水位库容约束、最大出力约束,最大出库流量约束等。
(2)
式中:
表示水电站m在t时刻的库容,
表示m的上游电站在
时刻的出库流量;
为上游出库到达下游时间;
;
、
与
分别表示梯级水电站m在时刻t的区间入流、出库、蒸发、渗漏损失的水量;
、
、
、
分别表示电站m出库下限、出库上限、水位上限、水位下限。
运行约束:
水电站在运行过程中需满足机组过流上下限约束、出力大小上下限约束:
(3)
式中
、
表示机组i最小、最大过流;
表示水电站m水电机组i在t时刻的出力。
2.2. 遗传算法改进策略
针对遗传算法易受初始值、交叉变异概率、精英种群的影响,通过以下三个方面对遗传算法进行改进。
a) Logistic映射提升初始种群质量
为了尽可能的提高种群搜索效率,本文采取Logistic映射的方式初始化种群,以提高种群的搜索效率。
(4)
其中:
为历经t次迭代产生的个体序列;
为正向可调参数。
研究表明,为了使Logistic映射为混沌映射,
,本文计算取
。由于生成的序列可能并不一定在原可行域中,因此需要将生成种群,限制在原可行域中,可按式(5)对生成的种群序列进行约束。
(5)
其中:
、
分别表示原优化变量上限、下限;
表示个体n的初始位置。
b) 交叉概率Pc与变异概率Pm的选取
交叉概率Pc的选取:
交叉概率Pc对新个体的产生至关重要,Pc值过大会导致遗传算法产生的新个体结构破坏,Pc值过小,不易产生新个体,遗传算法收敛速度较慢,不易于算法的快速收敛。若在前期Pc值相对较大这样产生新个体的速度也就越快,后期Pc值较小,可避免前次计算最优结果遭到破坏,为此本文提出一种自适应策略,使得Pc能自适应改变。
(6)
式中
为要交叉的两个个体适应度较大的适应度值;
为种群中最大的适应度值;
为每代群体的平均适应度值;
要变异个体的适应度值;
、
为正向可调参数,取
,
。
变异概率Pm的选取:
变异概率Pm偏小不容易产生新的个体,偏大就变成了随机搜索。因此采用下述方式对Pm进行计算。
(7)
式中
为要交叉的两个个体适应度较大的适应度值;
为种群中最大的适应度值;
为每代群体的平均适应度值;
要变异个体的适应度值;
与
为正向可调参数,取
,
。
c) 精英策略
为了不破坏适应度较高的个体,在交叉过程中对精英个体遗传信息进行保护,假设M1 (
)为适应度较大的精英个体,个体M1与M2交叉过程中采取如下策略:
(8)
式中:m为计算过程中总的迭代次数,j为当前迭代的次数,b为阈值。
式(8)成立则M1与M2执行交叉操作,式(8)不成立则不进行交叉。
2.3. 求解流程
1) 编码:采取实数编码的方式,对梯级水电站的水位进行编码。
2) 初始种群的产生,采用Logistic映射初始化种群。
3) 适应度评价,对个体进行解码处理,得到个体的表现型,采用发电量最大的形式对种群的适应度进行评价。
4) 选择,选择种群中适应度较高的个体,淘汰种群中适应度较差的个体,为了保持种群的规模一定,淘汰的个体由交叉和变异产生的新个体替代。
5) 交叉,交叉概率采用2.2提出的自适应策略,对种群中的所有个体进行随机配对,采用单点交叉的方式以概率Pc,随机交换个体中的部分染色体。
6) 变异,采用轮盘赌的方式确定要变异的个体,并在约束范围内随机改变梯级电站的水位。
7) 重复步骤1)~6)直到迭代结束,或最优解不再发生改变为止。
3. 算例分析
为了验证所提方法的有效性,以天生桥一级电站(下文称电站1)与天生桥二级电站(下文称电站2)为例,验证所提方法的有效性。其中电站1与电站2均以发电为主,电站1位于上游,装机容量为1200 MW的多年调节电站;电站2位于下游装机为1320 MW的日调节电站。
在调度中,梯级水电站各个参数设置如表1所示。采用改进前(下文称优化前)与改进后(下文称优化后)的遗传算法分别进行计算,初始种群规模设置与发电量的关系如图1(a)所示,初始种群规模设置为过大,求解过程中个别易主导全体解的进化方向,求解效率低下,规模过小收敛速度较慢,故初始种群规模设置为200;迭代次数与耗水量之间的关系如图1(b)所示,当迭代次数达到50时,算法已经收敛,在计算过程中,为了保证算法一定能够收敛,将迭代次数设置为500。所有仿真语言均采用Python语言进行编写,运行环境主频3.2 GHz、运行内存16 GB、硬盘大小500 GB、系统为Window系统的ThinkPad。仿真计算100次,最长计算时间59.30 s,可有效满足短期调度时效性要求。
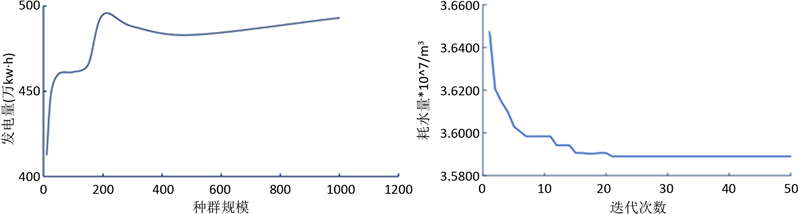
Figure 1. (a) Relationship between population size and power generation; (b) Relationship between iteration times and water consumption
图1. (a) 种群规模与发电量的关系;(b) 迭代次数与耗水量的关系
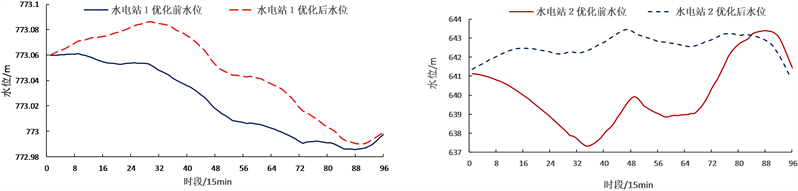
Figure 2. (a) Water level changes of Cascade Hydropower Station 1 before and after optimization; (b) Water level changes of Cascade Hydropower Station 2 before and after optimization
图2. (a) 梯级水电站1优化前后水位变化情况;(b) 梯级水电站2优化前后水位变化情况

Table 1. Operation parameters of cascade hydropower stations
表1. 梯级水电站运行参数
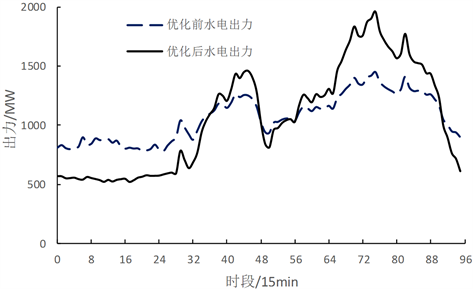
Figure 3. Output of cascade hydropower stations before and after optimization
图3. 优前后梯级水电站出力情况
图2展示了优化前后梯级水电站的水位变化,图3展示了梯级水电站出力变化情况,由图3可知,梯级水电站在优化前前期出力较大,导致后期出力不足,求解陷入局部最优;优化后梯级水电站在前期发电量较小,后期随着水位升高,平均耗水率减少,发电量增加。与优化前相比,优化后水电多发45.56万kW∙h,显著提高了发电效益。
基金项目
特别感谢“北京市水电水利规划设计总院水文气象及流域水电开发大数据平台第一阶段开发技术服务水利工程咨询项目”提供的资金支持。
参考文献