一类二阶非线性微分系统正解的存在唯一性
Existence and Uniqueness of Positive Solutions for a Class of Second-Order Nonlinear Differential Systems
DOI: 10.12677/PM.2021.116134, PDF, HTML,    国家自然科学基金支持
作者: 杨 阳：西北师范大学数学与统计学院，甘肃 兰州
关键词: Lipschitz条件；压缩映像原理；正解；Leray-Schauder抉择；Lipschitz Condition； Contraction Mapping Principle； Positive Solution； Leray Schauder’s Alternative
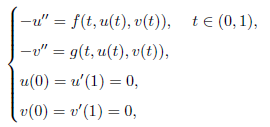
摘要: 本文利用 Leray-Schauder 抉择和 Banach 压缩映像原理研究了二阶微分系统 正解的存在唯一性, 其中f,g : [0,1] × [0,+∞) × [0,+∞) → [0,+∞) 连续.
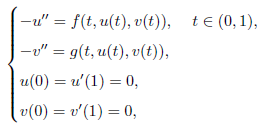
Abstract: In this paper, by using Leray-Schauder’s alternative and contraction mapping principle to study the positive solutions for a system of second-order boundary value problems where f,g : [0,1] × [0,+∞) × [0,+∞) → [0,+∞)  are continuous.
文章引用：杨阳. 一类二阶非线性微分系统正解的存在唯一性[J]. 理论数学, 2021, 11(6): 1211-1220. https://doi.org/10.12677/PM.2021.116134

参考文献

[1] Grigorian, G.A. (2021) On the Reducibility of Systems of Two Linear First-Order Ordinary Differential Equations. Monatshefte fu¨r Mathematik, 195, 107-117. [Google Scholar] [CrossRef] 
[2] Maksimov, V.I. (2021) The Methods of Dynamical Reconstruction of an Input in a System of Ordinary Differential Equations. Journal of Inverse and Ill-Posed Problems, 29, 125-156. [Google Scholar] [CrossRef] 
[3] Gainetdinova, A.A. and Gazizov, R.K. (2020) Integration of Systems of Two Second-Order Ordinary Differential Equations with a Small Parameter That Admit Four Essential Operators. Sibirskie E`lektronnye Matematicheskie Izvestiya, 17, 604-614. [Google Scholar] [CrossRef] 
[4] Filimonov, M.Yu. (2020) Global Asymptotic Stability with Respect to Part of the Variables for Solutions of Systems of Ordinary Differential Equations. Differential Equations, 56, 710-720. [Google Scholar] [CrossRef] 
[5] Ma, R.Y. (2000) Multiple Nonnegative Solutions of Second-Order System of Boundary Value Problem. Nonlinear Analysis: Theory, Methods and Applications, 42, 1003-1010. [Google Scholar] [CrossRef] 
[6] 王素云. 一类二阶常微分方程组边值问题的三个正解[J]. 应用泛函分析学报, 2000, 2(4): 349-352.
[7] 杨志林, 孙经先. 非线性二阶常微分方程组边值问题的正解[J]. 数学学报, 2000, 47(1): 111-118.
[8] Yang, Z.L., Wang, X.M. and Li, H.Y. (2020) Positive Solutions for System of Second-Order Quasilinear Boundary Value Problems. Nonlinear Analysis, 195, Article ID: 111749. [Google Scholar] [CrossRef] 
[9] 郭大均, 孙经先, 刘兆理, 非线性常微分方程泛函方法[M]. 第2版. 济南: 山东科学技术出版社, 2006.
[10] 郭大均. 非线性泛函分析[M]. 第2版. 济南: 山东科学技术出版社, 2003.

为你推荐