摘要:
在 2015 年,DP -染色(也叫对应染色)是由
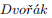
和 Postle 提出的有关列表染色推广。在 2019年,Bernshteyn,Kostochka,and Zhu 提出了 DP-染色的分数版本。 不像分数列表色数,一个图G的分数 DP -色数被记为
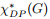
,可以任意大比它的分数色数。
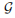
是一些图所构成的集族,它的分数 DP -色数是这些图中分数 DP -色数的上确界。 我们把围长至少为 t 的一类串井联图记为Qt。这篇论文证明了对于t = 4q − 1, 4q, 4q + 1, 4q + 2,Qt 的分数 DP -色数为 2 + 1。
Abstract:
DP-coloring (also called correspondence coloring) is generalization of list coloring in- troduced by
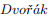
and Postle in 2015. In 2019, Bernshteyn,Kostochka,and Zhu introduced a fractional version of DP-coloring. Unlike the fraction list chromatic number, the fractional DP-chromatic number of a graph G,denoted
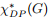
,can be arbitrarily larger than χ∗(G). The fractional DP-chromatic number of a family G of graphs is the supremum of the fractional DP-chromatic number of graphs in
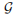
. We denote by Qt the class of series-parallel graphs with girth at least t. This paper proves that for t = 4q − 1, 4q, 4q + 1, 4q + 2, the fractional DP-chromatic number of Qt is exactly 2 + 1 .