n-强-F-Ding投射模

n-Strongly-F-Ding Projective Modules

摘要: 引入n-强-F-Ding投射模，给出n-强-F-Ding投射模的等价刻画和基本性质，证明了一个模M是n-强-F-Ding投射模当且仅当M同构于某个n-强-F-Ding投射模与投射模的直和。

Abstract: In this paper, we introduce n-Strongly-F-Ding projective module, give its equivalent characteriza-tion and basic properties, and prove that a module is n-Strongly-F-Ding projective module if and only if it is isomorphic to a direct sum of a n-Strongly-F-Ding projective module and a projective module.

1. 引言

1995年，在文献 [1] 中，Enochs等人在任意结合环上引入了Gorenstein投射(内射，平坦)模的定义，推广了G-维数为0的有限生成模。2007年，Bennis和Mahdou在文献 [2] 中，引入了特殊的Gorenstein模，即强Gorenstein投射(内射，平坦)模的概念，给出强Gorenstein投射模的等价刻画，并且证明了一个模M是Gorenstein投射模当且仅当它是某个强Gorenstein投射模的直和项。在文献 [3] 中，Zhao和Huang引入n-强Gorenstein投射(内射，平坦)模的概念，研究这类模的性质。

2009年，在文献 [4] 中，Mao和Li等定义了强Gorenstein平坦模，即Ding投射模。证明了在凝聚环下，Ding投射模是Gorenstein平坦模。同年在文献 [5] 中，Xing定义了n-强Ding投射模的概念，证明了在交换环的情况下，一个模M是n-强Ding投射模，那么模M与投射模的张量是n-强Ding投射模。

2011年，在文献 [6] 中，作者引入了X-Gorenstein投射和Y-Gorenstein内射(平坦)模及它们的维数，研究了这类模的性质，给出了X-Gorenstein投射和Y-Gorenstein内射(平坦)维数的等价条件。

受以上启发，本文引入n-强-F-Ding投射模，研究它的性质，并给出它的等价条件。

本文中的环R均指有单位元的结合环，模指左R-模。Proj，Flat分别表示投射模类，平坦模类。

2. 预备知识

定义1.1 [1] 称R-模M是Gorenstein投射模，如果存在投射模的正合序列

$\cdots \stackrel{f_{-1}}{\to }{P}_{-1}\stackrel{f_0}{\to }{P}_0\stackrel{f_1}{\to }{P}_1\stackrel{f_2}{\to }\cdots$，

其中 $\forall P_i\in \text{Proj}$，使得 $M\cong \text{Ker}\left(P_1\to P_0\right)$，且对 $\forall P\in \text{Proj}$， ${\text{Hom}}_R\left(-,P\right)$ 保持以上序列正合。记M为GP模。所有GP模的类记为 $\text{GP}\left(\text{R}\right)$。

定义1.2 [4] 称R-模M是Ding投射模，如果存在投射模的正合序列

$\cdots \stackrel{f_{-1}}{\to }{P}_{-1}\stackrel{f_0}{\to }{P}_0\stackrel{f_1}{\to }{P}_1\stackrel{f_2}{\to }\cdots$，

其中 $\forall P_i\in \text{Proj}$，使得 $M\cong \text{Ker}\left(P_1\to P_0\right)$，且对 $\forall L\in \text{Flat}$， ${\text{Hom}}_R\left(-,\text{L}\right)$ 保持以上序列正合。记M为Ding投射模。所有Ding投射模的类记为 $\text{DP}\left(\text{R}\right)$。

定义1.3 [6] 设n是正整数。称R-模M是n-强Ding投射模，如果存在R-模的正合序列

$0\stackrel{}{\to }M\stackrel{f_n}{\to }{P}_{n-1}\stackrel{f_{n-1}}{\to }\cdots \stackrel{f_1}{\to }{P}_0\stackrel{f_0}{\to }M\stackrel{}{\to }0$，

其中 $\forall P_i\in \text{Proj}$，且对 $\forall L\in \text{Flat}$， ${\text{Hom}}_R\left(-\text{,L}\right)$ 保持以上序列正合。记M为 $n\text{-SDP}$ 模。所有 $n\text{-SDP}$ 模的类记为 $n\text{-SDP}\left(\text{R}\right)$。

注： $\text{P}\left(\text{R}\right)\subseteq n\text{-SDP}\left(\text{R}\right)\subseteq \text{DP}\left(\text{R}\right)\subseteq \text{GP}\left(\text{R}\right)$。

3. 主要结果

定义2.1 设n是正整数，F是包含所有平坦模的类，称R-模M是n-强-F-Ding投射模，如果存在R-模的正合序列

$0\stackrel{}{\to }M\stackrel{f_n}{\to }{P}_{n-1}\stackrel{f_{n-1}}{\to }\cdots \stackrel{f_1}{\to }{P}_0\stackrel{f_0}{\to }M\stackrel{}{\to }0$，

其中 $\forall P\in \text{Proj}$，且对 $\forall \text{F}\in F$， ${\text{Hom}}_R\left(-,\text{F}\right)$ 保持以上序列正合。记M为 $n\text{-}S\text{-}F\text{-}DP$ 模。所有 $n\text{-}S\text{-}F\text{-}DP$ 模的类记为 $n\text{-}S\text{-}F\text{-}DP\left(R\right)$。

注1： $\text{Proj}\subseteq n\text{-}S\text{-}F\text{-}DP\left(R\right)\subseteq n\text{-SDP}\left(\text{R}\right)$。

命题2.2 设 ${\left\{M_j\right\}}_{j\in I}$ 是一簇 $n\text{-}S\text{-}F\text{-}DP$ 模，那么 ${\oplus }_{j\in I}{M}_{j\in I}$ 是 $n\text{-}S\text{-}F\text{-}DP$ 模。

证 通过定义对 $\forall j\in I$ 有正合列

$0\stackrel{}{\to }{M}_j\stackrel{}{\to }{P}_{n-1}^j\stackrel{}{\to }\cdots \stackrel{}{\to }{P}_0^j\stackrel{}{\to }{M}_j\stackrel{}{\to }0$，

其中 $\forall P_i^j\in \text{Proj}$，对 $\forall \text{F}\in F$， $\text{Hom}\left(-,\text{F}\right)$ 作用下依旧正合。所以有正合列

$0\stackrel{}{\to }{\oplus }_{j\in I}{M}_j\stackrel{}{\to }{\oplus }_{j\in I}{P}_{n-1}^j\stackrel{}{\to }\cdots \stackrel{}{\to }{\oplus }_{j\in I}{P}_0^j\stackrel{}{\to }{\oplus }_{j\in I}{M}_j\stackrel{}{\to }0$，

其中 $\forall {\oplus }_{j\in I}{P}_i^j\in \text{Proj}$，对 $\forall \text{F}\in F$， $\text{Hom}\left(-,\text{F}\right)$ 作用下依旧正合。通过定义知 ${\oplus }_{j\in I}{M}_j$ 是 $n\text{-}S\text{-}F\text{-}DP$ 模。

引理2.3 如果存在正合列

$0\stackrel{}{\to }M\stackrel{h_n}{\to }{P}_{n-1}\stackrel{h_{n-1}}{\to }\cdots \stackrel{h_1}{\to }{P}_0\stackrel{h_{\backslash 0}}{\to }M\stackrel{}{\to }0$，

其中 $\forall P_i\in \text{Proj}$ 且 $M\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$，那么 $\forall \mathrm{Im}{h}_i\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$。

对照文献 [7] 的定义我们可以定义R-模M的F-投射维数 $F\text{-}pd\left(M\right)=\inf \left\{n|存在F\text{-}分解0\stackrel{}{\to }{\text{F}}_n\stackrel{}{\to }\cdots \stackrel{}{\to }{\text{F}}_{\text{0}}\stackrel{}{\to }M\stackrel{}{\to }0，其中\forall {\text{F}}_i\in F\right\}$。当n不存在时记 $F\text{-}\dim =\infty$，下面给出n-强F-Ding投射模的等价刻画：

命题2.4 n是正整数，设M是R-模，则以下等价：

1) $M\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$。

2) 存在R-模的短正合列

$0\stackrel{}{\to }M\stackrel{f_n}{\to }{P}_{n-1}\stackrel{f_{n-1}}{\to }\cdots \stackrel{f_1}{\to }{P}_0\stackrel{f_{\backslash 0}}{\to }M\stackrel{}{\to }0$，

其中 $\forall P_i\in \text{Proj}$，且对 $\forall F\text{-}pd\left(H\right)<\infty$， $Ex{t}_R^{i>0}\left(M,H\right)=0$。

3) 存在R-模的短正合列

$0\stackrel{}{\to }M\stackrel{f_n}{\to }{P}_{n-1}\stackrel{f_{n-1}}{\to }\cdots \stackrel{f_1}{\to }{P}_0\stackrel{f_0}{\to }M\stackrel{}{\to }0$，

其中 $\forall P_i\in \text{Proj}$，且对 $\forall \text{F}\in F$， $Ex{t}_R^{i>0}\left(M,\text{F}\right)=0$。

证 $(1)\iff (3)$， $(2)\Rightarrow (3)$ 显然。现在证 $(3)\Rightarrow (2)$。

假设 $\forall F\text{-}pd\left(H\right)=m<\infty$。则有正合列

$0\stackrel{}{\to }{\text{F}}_m\stackrel{}{\to }{\text{F}}_{m-1}\stackrel{}{\to }\cdots \stackrel{}{\to }{\text{F}}_0\stackrel{}{\to }H\stackrel{}{\to }0$，

其中 $\forall {\text{F}}_i\in F$。取 $k_i=Ker\left({\text{F}}_i\to {\text{F}}_{i-1}\right)$， $i=0,1,\cdots ,m-3,m-2$，其中 ${\text{F}}_{-1}=H$ 则有短正合列

$0\to k_0\to {\text{F}}_0\to H\to 0$， ${\left(1\right)}^0$

$0\to k_1\to {\text{F}}_1\to k_0\to 0$， ${\left(2\right)}^0$

$\cdots$

$0\to k_{m-2}\to {\text{F}}_{m-2}\to k_{m-3}\to 0$， ${\left(m-1\right)}^0$

$0\to {\text{F}}_m\to {\text{F}}_{m-1}\to k_{m-2}\to 0$， ${\left(m\right)}^0$

对短正合列 ${\left(1\right)}^0,{\left(2\right)}^0,\cdots ,{\left(m-1\right)}^0,{\left(m\right)}^0$ 用 ${\text{Hom}}_R\left(M,-\right)$ 作用并由长正合列定理及维数转移可得

$Ex{t}_R^{m+j}\left(M,F_m\right)\cong Ex{t}_R^j\left(M,H\right)=\text{0}$，

故 $Ex{t}_R^{i>0}\left(M,H\right)=\text{0}$。

我们回顾一下投射可解的定义，称R-模类X是投射可解的，那么对于R-模的短正合列 $0\to A\to B\to C\to 0$，若 $C\in X$，则 $B\in X$ 当且仅当 $C\in X$。而我们知道n-强Gorenstein模类通常情况下并不投射可解。那么我们思考当在什么情况下有相似于投射可解的结论呢？于是我们有如下结果：

命题2.5 设 $0\to N\to M\to P\to 0$，是R-模的短正合列，其中P是投射模，则 $N\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$ 当且仅当 $M\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$。

证 $\Rightarrow )$ 因为 $N\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$，则通过定义存在R-模的正合列

$0\stackrel{}{\to }N\stackrel{}{\to }{P}_{n-1}\stackrel{}{\to }\cdots \stackrel{}{\to }{P}_0\stackrel{}{\to }N\stackrel{}{\to }0$，

其中 $\forall P_i\in \text{Proj}$，且对 $\forall \text{F}\in F$， $\text{Hom}\left(-,\text{F}\right)$ 作用下依旧正合。那么有R-模的正合列

$0\stackrel{}{\to }N\oplus P\stackrel{}{\to }{P}_{n-1}\oplus P\stackrel{}{\to }\cdots \stackrel{}{\to }{P}_0\oplus P\stackrel{}{\to }N\oplus P\stackrel{}{\to }0$，

通过定义知 $N\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$。

$\Leftarrow )$ 由于 $M\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$，且 $M\cong N\oplus P$，则通过定义知存在R-模的正合列

$0\stackrel{}{\to }N\oplus P\stackrel{f_n}{\to }{P}_{n-1}\stackrel{f_{n-1}}{\to }\cdots \stackrel{f_1}{\to }{P}_0\stackrel{f_0}{\to }N\oplus P\stackrel{}{\to }0$，

取 $M_1=Ker{f}_0$， $M_{n-1}=coKer{f}_n$，由引理2.4 $M_0,M_{n-2}\in n\text{-}S\text{-}F\text{-}DP\left(R\right)\subseteq DP\left(R\right)$。

由推出图

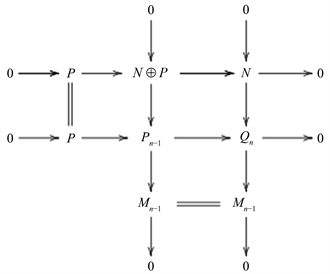
考虑短正合列

$0\stackrel{}{\to }N\stackrel{}{\to }{Q}_n\stackrel{}{\to }{M}_{n-1}\stackrel{}{\to }0$，

用 $\text{Hom}\left(-,P\right)$ 作用并由长正合列定理以及维数转移可得

$Ex{t}_R^1\left(Q_n,P\right)\cong Ex{t}_R^1\left(N,P\right)$

因为 $M\cong N\oplus P\in n\text{-}S\text{-}F\text{-}DP\left(R\right)\subseteq n\text{-}SDP\left(R\right)\subseteq DP\left(R\right)\subseteq GP\left(R\right)$，则

$Ex{t}_R^1\left(N\oplus P,P\right)=Ex{t}_R^1\left(N,P\right)\oplus Ex{t}_R^1\left(P,P\right)=0$

所以 $Ex{t}_R^1\left(Q_n,P\right)=0$。即中间行的正合列可裂，可得 $Q_n\in \text{Proj}$，且有短正合列

$0\stackrel{}{\to }N\stackrel{}{\to }{Q}_n\stackrel{}{\to }{M}_{n-1}\stackrel{}{\to }0$

对 $\forall \text{F}\in F$， $\text{Hom}\left(-,\text{F}\right)$ 作用下依旧正合。

由拉回图

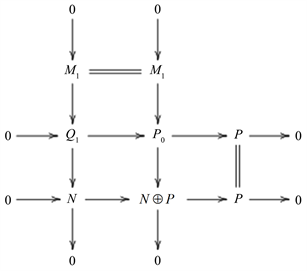
考虑到短正合列 $0\stackrel{}{\to }{Q}_1\stackrel{}{\to }{P}_0\stackrel{}{\to }P\stackrel{}{\to }0$ 可裂，可得 $Q_1\in \text{Proj}$。且有短正合列

$0\stackrel{}{\to }{M}_1\stackrel{}{\to }{Q}_1\stackrel{}{\to }N\stackrel{}{\to }0$，

对 $\forall \text{F}\in F$， $\text{Hom}\left(-,\text{F}\right)$ 作用下依旧正合。从而有正合列

$0\stackrel{}{\to }N\stackrel{}{\to }{Q}_{n-1}\stackrel{}{\to }{P}_{n-2}\stackrel{}{\to }\cdots \stackrel{}{\to }{P}_0\stackrel{}{\to }{Q}_1\stackrel{}{\to }N\stackrel{}{\to }0$，

对 $\forall \text{F}\in F$， $\text{Hom}\left(-,\text{F}\right)$ 作用下依旧正合。

命题2.6 设 $0\stackrel{}{\to }N\stackrel{}{\to }P\stackrel{}{\to }M\stackrel{}{\to }0$， $P\in \text{Proj}$ 是R-模的短正合列。若 $M\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$，则 $N\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$。

证 由于 $M\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$，则存在R-模的正合列

$0\stackrel{}{\to }M\stackrel{g_n}{\to }{P}_{n-1}\stackrel{g_{n-1}}{\to }\cdots \stackrel{g_1}{\to }{P}_0\stackrel{g_0}{\to }M\stackrel{}{\to }0$，

其中 $\forall P_i\in \text{Proj}$，取 $M_1=Ker{g}_0$，由引理2.3知 $M_1\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$。

考虑拉回图

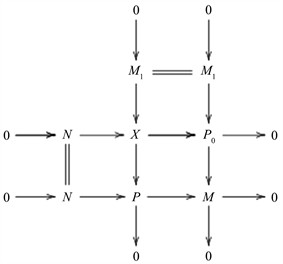
因为短正合列 $0\stackrel{}{\to }{M}_1\stackrel{}{\to }X\stackrel{}{\to }P\stackrel{}{\to }0$ 可裂，所以 $X\cong M_1\oplus P\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$，由命题2.4知 $N\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$。

推论2.7 设 $0\to N\to P\to M\to 0$，是R-模的短正合列，其中 $P\in \text{Proj}$，则 $N\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$ 当且仅当 $M\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$。

命题2.8 设R是交换环， $Q\in \text{Proj}$。若 $M\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$，则 $M{\otimes }_{R}Q\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$。

证 因为 $M\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$，则存在R-模的正合列

$0\stackrel{}{\to }M\stackrel{}{\to }{P}_{n-1}\stackrel{}{\to }\cdots \stackrel{}{\to }{P}_0\stackrel{}{\to }M\stackrel{}{\to }0$，

其中 $\forall P_i\in \text{Proj}$，那么

$0\stackrel{}{\to }M{\otimes }_{R}Q\stackrel{}{\to }{P}_{n-1}{\otimes }_{R}Q\stackrel{}{\to }\cdots \stackrel{}{\to }{P}_0{\otimes }_{R}Q\stackrel{}{\to }M{\otimes }_{R}Q\stackrel{}{\to }0$，

因为R是交换环，所以 $\forall P_i{\otimes }_{R}Q\in \text{Proj}$，由于

$Ex{t}_R^i\left(M\otimes Q,F\right)\cong Ho{m}_R\left(Q,Ex{t}_R^i\left(M,F\right)\right)=\text{0}$，

通过命题2.3知 $M{\otimes }_{R}Q\in n\text{-}S\text{-}F\text{-}DP\left(R\right)$。