基于COT模式的THD补偿方法研究

Research on THD Compensation Method Based on COT Mode

摘要: 近年来，在照明应用的领域中，LED以其高效率、节能的特点掀开了人类照明历史上的崭新篇章，随着人们对LED越来越高的应用要求，LED驱动器逐渐成为LED发展的瓶颈，与此同时分次谐波或总谐波失真已经成为定义LED驱动器性能的非常重要的指标之一。针对LED驱动器领域中总谐波失真严重而引起的污染和效率等问题，本文提出了两种补偿电路，此电路在传统恒导通时间控制模式的基础上，对决定LED输出电流的采样电阻上的电压进行采集并分别转换为电压和电流补偿。通过Mathcad软件计算以及Simplis仿真分析以及实验验证表明，此补偿方法可优化总谐波失真。在220 V AC输入电压时，总谐波失真可达到小于10%的效果。

Abstract: In recent years, in the field of lighting application, LED has opened a new chapter in the history of human lighting with its high efficiency and energy saving characteristics. With the increasing ap-plication requirements of LED, the performance requirements of LED drivers have gradually developed into the bottleneck of LED. The fractional harmonic or Total Harmonic Distortion (THD) has become one of the most important indicators to define the performance of LED drivers. In order to solve the pollution and efficiency problems caused by the serious total harmonic distortion in the field of LED driver, two compensation circuits are proposed in this paper. Based on the tradi-tional constant-on-time control mode, this circuit collects the voltage on the sampling resistance which determines the output current of the LED and converts it into voltage and current compensation respectively. The results of Mathcad software calculation, Simplis simulation analysis and ex-perimental verification show that this compensation method can optimize the total harmonic dis-tortion. At the input voltage of 220 VAC, the THD can be less than 10%.

1. 引言

LED驱动技术是当前的研究热点之一 [1]。Buck拓补在LED驱动器的研究领域中因其在整个输入电压范围内保持一个较高的效率 [2]，同时具有共模噪声小、体积小且成本低等特点，因此获得了广泛的应用。然而在Buck拓补中，当输入电压低于输出电压时功率管不导通，输入电流会形成断崖式下跌，造成了谐波分量大、总谐波失真(Total Harmonic Distortion, THD)升高的问题。输入电流的分次谐波中，尤其是高次谐波，会对电网产生影响甚至是污染。文献 [3] 通过辅助绕组调制前馈电流来减弱谐波失真的程度，但随着频率的升高增加了失真程度，限制了临界导通模式的应用；文献 [4] 通过调整功率管开通时间和频率来最大限度地降低THD，伴随的是输出电压纹波的升高，且电路复杂。本文提出的Buck拓补的LED驱动器采用恒导通模式(Constant on-time, COT)作为系统控制模式来改善分次谐波的问题 [5]，其基本思想是使电感电流工作在临界导通模式 [6]，使输入电流跟随输入电压，达到低的谐波失真效果，同时简化了环路补偿电路，提高系统整体效率。本文先是讨论了COT控制模式的原理，分析了COT模式下THD差的原因，近而提出了两种THD补偿的控制方法优化THD，同时利用Mathcad计算分析预期以及Simplis仿真验证，结果都证明了此方法的正确性和可行性。

2. COT控制模式

图1为恒导通模式控制的原理图，其普遍应用于电感临界导通模式，即当电感电流到零后立即打开功率管，同时使每个周期的开通时间T_on恒定 [7]。其工作原理大致如下：系统上电后对Comp电容充电到初始值Comp_ini，初始值所对应的Ton_ini作为初始T_on开启功率管，电感电流上升，采样电阻R_cs采样电感电流并在其两端产生V_cs，V_cs经过采样保持后作为误差放大器的输入端，输入另一端为固定的基准V_ref，误差放大器放大两者的差值后作为Comp电压。

由于Comp电容较大，因此可视作半周期内Comp电压是恒定的。又因Buck拓补中输出电流中的高频分量大多被输出电容吸收，因此输出电流近似为电感平均电流，近而有如下输出电流公式：

$I_{out}\left(\theta \right)=\frac{1}{\pi }{\displaystyle \underset{{\theta }_0}{\overset{{\theta }_1}{\int }}\frac{I_{pk}\left(\theta \right)}{2}\text{d}\theta }=\frac{1}{\pi }{\displaystyle \underset{{\theta }_0}{\overset{{\theta }_1}{\int }}\frac{V_{in}\left(\theta \right)-V_{out}}{2L_m}\ast T_{on}\text{d}\theta }$ (1)

当V_ref > V_cs时，误差放大器电流给Comp电容充电，Comp电压升高；当V_ref < V_cs时，误差放大器电流给Comp电容放电，Comp电压降低；电容充电的能量与放电的能量守恒，因此有如下表达式：

${\displaystyle \underset{T_{\text{1}}}{\overset{T_{\text{3}}}{\int }}{G}_m\ast \left(V_{ref}-V_{cs}\right)\text{d}t}=0$ (2)

由公式(2)可知，输出电流的平均值近似为芯片内部基准与采样电阻的比值，因此可保持输出电流恒定，与芯片外围参数和其他因素无关，达到了恒流的目的。然后又将Comp电压与芯片内部固定锯齿波Ramp做比较，如图2，当Ramp与Comp电压相等时，关断功率管，输出PWM控制信号驱动功率管关闭，完成对系统的闭环控制。

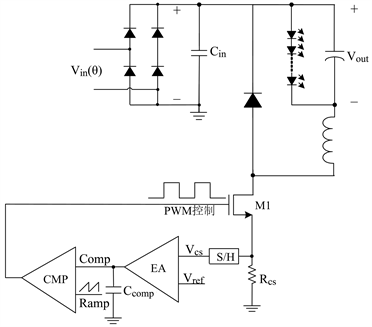
Figure 1. Principle of COT control mode

图1. COT控制模式原理框图

Figure 2. Comp vs Ramp

图2. Comp与斜坡电压Ramp比较

从整个系统来看，功率管开通时，当输入电压大于输出电压后，功率管开启，采样R_cs电压，首先设输入电压关于θ的表达式为：

$V_{in}\left(\theta \right)=V_{inm}\ast \sin \left(\theta \right)$ (3)

其中θ = wt，w = 2πf，V_inm为输入峰值电压。由于Buck拓补只在输入电压大于输出电压时才有电流输出，即

$V_{inm}\ast \sin \left(\theta \right)\text{>}{V}_{out}$ (4)

因此系统工作有导通角影响，导通角外即死区，导通角(θ₀, θ₁)的范围如下：

$\begin{array}{l}{\theta }_0=\arcsin \left(V_{out}/V_{inm}\right)\\ {\theta }_1=\pi -{\theta }_0\end{array}$ (5)

即导通角范围为 $\left({\theta }_0,\pi -{\theta }_0\right)$，Buck拓补功率管开通后，由伏秒平衡可知，

$L_m\frac{\text{d}{I}_{pk}\left(\theta \right)}{T_{on}}=V_{in}\left(\theta \right)-V_{out}$ (6)

电感电流上升的斜率为 $\left(V_{in}\left(\theta \right)-V_{out}\right)/L_m$，则电感电流的峰值为：

$I_{pk}\left(\theta \right)=\frac{V_{in}\left(\theta \right)-V_{out}}{L_m}\ast T_{on}$ (7)

关断时间T_off由系统参数决定

$T_{off}\left(\theta \right)=\frac{L_m\ast I_{pk}\left(\theta \right)}{V_{out}}$ (8)

当θ在 $\left({\theta }_0,\pi -{\theta }_0\right)$ 内时，占空比近似为

$D\left(\theta \right)=V_{out}/V_{inm}\ast \sin \left(\theta \right)$ (9)

输入平均电流表达式为

$I_{in}\left(\theta \right)=\frac{I_{pk}\left(\theta \right)}{2}\ast D\left(\theta \right)$ (10)

结合公式(7)和公式(9)，则输入电流跟随θ的表达式如下

$I_{in}\left(\theta \right)=\{\begin{array}{l}\frac{\left[V_{inm}\left(\theta \right)-V_{out}\right]\ast V_{out}\ast T_{on}}{2\ast L_m\ast V_{inm}\left(\theta \right)},\left({\theta }_{\text{0}},\pi -{\theta }_{\text{0}}\right)\\ \text{0,otherwise}\end{array}$ (11)

公式(11)中，假设V_out和L_m都近似不变，如能控制T_on补偿不变，即可实现输入电流跟随输入电压达到输入电流正弦化的目的，达到了功率因数校正的目的 [8]。下图3为COT控制模式系统理想波形：

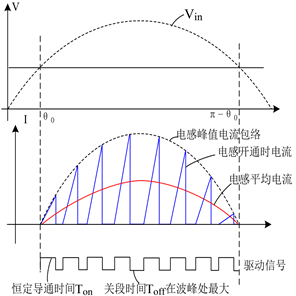
Figure 3. Waveform of COT control mode

图3. COT控制模式系统波形

3. 基于Mathcad计算的THD补偿方法

上文说明了采用恒定导通模式作为控制模式的原理，但通过仿真验证，仅仅采用COT模式，输入电流会存在畸变。下图是基于Mathcad仿真在COT控制模式下输入电流与理想输入电流对比，系统方案采用220 Vac输入，输出电压72 V，电流240 mA。由图4可见，仿真的输入电流波形与理想输入电流波形相比，有以下两个特点：1) 呈现波峰下陷，波谷陡峭的形状。2) 在交越处有失真，电流为零 [9]。

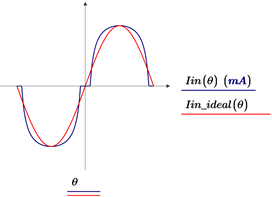
Figure 4. Input current distortion diagram based on Mathcad

图4. 基于Mathcad仿真COT控制模式输入电流失真图

基于图4，可分析造成这两个特点即失真的主要原因。其一，过零处交越失真是因为输入电压低于输出电压时功率管不导通，此为Buck拓补本身的限制。另外在谷底处由于检测不到退磁，输入电流会形成断崖式下跌，谷底近似为零，这时可设置芯片的最小关断时间，使谷底工作在高频状态，优化交越失真引起的THD影响，此优化方式简单，文本不做详细说明。

采用COT控制模式在Mathcad中对输入电压从176~265 Vac范围内仿真THD，下图为输入220 Vac时计算THD结果(图5)：

Figure 5. COT mode THD calculation based on Mathcad

图5. COT模式基于Mathcad THD计算

同样采用此算法在Mathcad中对输入电压从176~265 Vac范围内仿真THD如下表1所示：

Table 1. THD simulation value in COT control mode

表1. COT控制模式下的THD仿真值

其中，Buck拓补中占空比近似为

$D\left(\theta \right)=V_{out}/V_{inm}\ast \sin \left(\theta \right)$ (12)

说明了当θ在 $\left({\theta }_0,\pi -{\theta }_0\right)$ 内时，由式(12)可知，占空比是随θ变化的，利用Mathcad仿真占空比波形如图6：

Figure 6. Mathcad duty cycle with θ

图6. 占空比随θ变化图

由图6可见，占空比在波峰时最小，波谷时最大，因此输入电流会在波峰时最扁平，波谷时最陡峭，由此可得到图4的电流波形。由于失真的影响，输入电流偏离正弦曲线，会导致THD差 [10] [11]，因此需要一种补偿方式将输入电流的波峰值抬高，波谷压低，以达到接近于正弦的目的，改善THD。参考文献 [12] 中提出在隔离flyback拓扑在CCM模式下采用变开启时间的控制方法，本文在此思想的基础上，通过采样Vcs的峰值补偿到Comp或斜坡电压上，以此优化THD。下面来详细介绍两种补偿方法。

3.1. 电压型补偿方法

图7为电压型补偿原理框图，其原理为采样R_cs两端的峰值电压，一部分与芯片内部基准做差值输入内部的误差放大器中，一部分进入采样保持电路，保持采样到的峰值电压Vcs_pk，再经过电压电流转换网络转换成补偿电压，把此电压补偿在Comp电压的初值Comp_ini上，可使Comp电压升高。

Comp电压升高后，与同样的斜坡比较时，斜坡电压需要达到更高的Comp电压才能关断功率管，因此同样起到了增大T_on的效果。如图8所示：

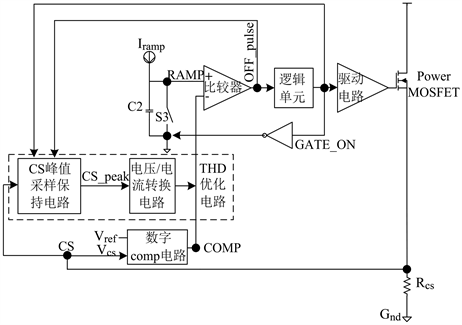
Figure 7. Voltage-type compensation block diagram

图7. 电压型补偿原理框图

Figure 8. Comp vs Ramp in voltage-type compensation

图8. 电压型补偿Comp和Ramp比较

波峰的峰值最高，因此电流补偿的最多，即波峰的T_on增加的最多；波谷的峰值低，补偿的电流少，因此谷底的T_on相对波峰的增量少，可弥补由占空比带来的输入电流波峰下陷，波谷陡峭的问题。T_on可用表达式表示为

$T_{on}=\frac{C_2\ast \left(V_{comp}-V_{comp\text{\_}ini}+k\ast \frac{V_{cs\text{\_}pk}}{R_{cs}}\right)}{I_{ramp}}$ (13)

其中k为补偿系数，在Mathcad将电压型补偿的算法拟合，仿真THD数值如下表2。

Table 2. THD simulation value in voltage-type compensation

表2. 电压补偿型下的THD仿真值

3.2. 电流型补偿方法

图9为电流型补偿原理框图，补偿方式为采样电阻两端的峰值电压，经过网络转换成补偿电流，把此电流补偿在Ramp的斜坡电流上可使斜坡电流减小，Ramp斜率变缓。

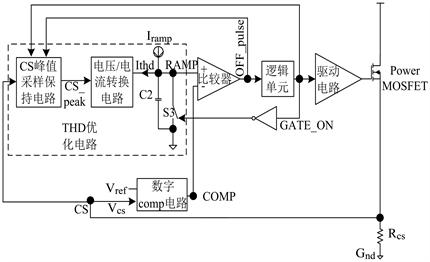
Figure 9. Current-type compensation block diagram

图9. 电流型补偿原理框图

斜坡电压斜率变缓后，斜坡电压与Comp电压相比进行T_on的调制，在此补偿方式下，斜坡电压与Comp电压相比后会延长T_on，如图10所示。

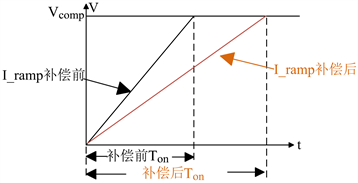
Figure 10. Comp vs Ramp in current-type compensation

图10. 电流型补偿Comp和Ramp比较

此补偿方式同样采取波峰补偿的T_on多，波谷补偿的T_on少，T_on可用表达式表示为

$T_{on}=\frac{C_{\text{2}}\ast \left(V_{comp}-V_{comp\text{\_}ini}\right)}{I_{ramp}-k\ast \frac{V_{cs\text{\_}pk}}{R_{cs}}}$ (14)

其中k为补偿系数，将电流型补偿的算法拟合，在Mathcad中仿真THD数值如表3。

Table 3. THD simulation value in current-type compensation

表3. 电流补偿型下的THD仿真值

从表2和表3可知，电压型和电流型补偿均能降低THD，改善输入电流的失真问题，以达到降低THD的效果。但比较两种输入电流补偿方式，从电路复杂程度来看，电路中叠加电流比叠加电压的方式简单，电路更容易实现。

3.3. 基于Simplis仿真验证

Mathcad软件是纯理论计算的工具，考虑到实际应用有其小信号场景以及拟合T_on的算法有一定的误差，因此使用Simplis软件进一步接近实际中搭建了Buck的闭环控制模型，并把THD补偿的算法分别加入到环路中仿真THD，搭建原理图如下(图11)，系统方案采用220 Vac输入，输出电压72 V，输出电流240 mA：

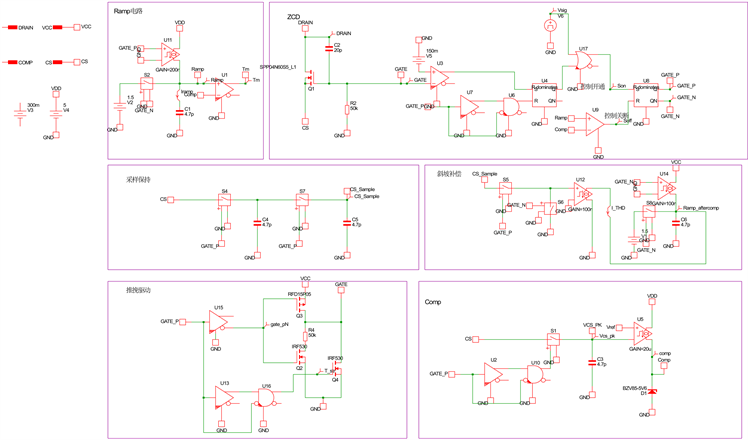
Figure 11. Closed-loop model based on Simplis

图11. Simplis搭建闭环模型

采用电压型THD补偿电路，仿真输入电流的THD如下图：

Figure 12. THD simulation on voltage-type

图12. 电压型补偿THD仿真

从图12 Simplis仿真结果显示，采用电压型THD补偿可将THD优化至10.998%，比Mathcad计算值落差。

Figure 13. THD simulation on voltage-type

图13. 电流型补偿THD仿真

图13为电流型Simplis仿真结果，结果显示采用电流型THD补偿可将THD优化至10.643%，通过Simplis仿真验证补偿电路的可行性和合理性。

4. 实验验证

为了进一步验证THD理论分析的正确性，两种补偿方式的芯片流片封装后按照图14典型的非隔离Buck LED驱动电路搭建外围应用，分别测试电压型和电流型THD补偿方式的THD实测值。

Figure 14. Peripheral design schematic diagram

图14. 外围设计原理图

图14中，输入加π型滤波器对策EMI，DR脚为芯片内置功率mos漏极端，CS为采样引脚，Pow为供电引脚，基准为芯片GND。

Table 4. THD measured value in voltage-type compensation

表4. 电压补偿型下的THD实测值

在176~265 Vac的输入电压范围下测试电流型THD补偿系统板THD参数，如表5所示：

Table 5. THD measured value in current-type compensation

表5. 电流补偿型下的THD实测值

表4和表5可以看出，电压型和电流型THD补偿的实测结果与仿真结果相符，较只采用COT控制模式能够将THD优化5%~7%，如适当调整THD补偿系数，可将THD继续优化至更优值。在输入电压176~265 Vac范围内，THD低于14%，220 Vac输入电压下，THD可达到小于10%的效果，是LED驱动领域中较为理想的结果。

5. 结论

本文在分析传统COT控制模式THD差原因的基础上，提出了两种THD补偿方法，改善传统COT由于交越失真和占空比影响引起的THD高的问题，并通过Mathcad理论计算THD值，同时为验证补偿的精确性，利用Simplis软件搭建了仿真模型，Simplis模型仿真证明在合理的补偿参数下，THD均小于15%。最后，实验验证了应用本文提出的两种方法后，在176~265 Vac的输入电压范围下，可达到THD小于14%的效果，220 Vac输入电压下，THD可达到小于10%的效果，在实际工程中有一定的应用价值，值得推广与研究。