1. 引言
表面偏析是指溶质原子由体内聚集到表面的现象 [1],在合金材料中极为常见。它能改变材料的电子稳定性和化学性能 [2] [3]。在超薄薄膜材料中,由于处于表面的原子占了系统总原子的大部分,所以薄膜材料中的表面偏析起着重要的作用。人们对块体材料中表面偏析现象的研究已经有100多年的历史,Gibbs预言了表面偏析现象,并且提出恒温吸收理论去描述表面偏析 [4]。1988年,Du Plessis和G. N. van Wyk基于达肯的“上坡”扩散理论提出了修正达肯模型 [5],该模型由规则溶液模型发展而来,提出了偏析驱动力是化学势梯度,并成功地描述了体块材料平衡态和动态的表面偏析 [6] [7]。
薄膜材料中的偏析不同于块体材料,主要原因如下 [8]:1) 与块体材料相比,薄膜材料中偏析原子的数量有限,溶质原子偏析到表面后会严重改变其体内的浓度;2) 绝大多数的薄膜材料都需要沉积在衬底上,薄膜与衬底的界面亦是溶质原子偏析的一个潜在位置,溶质原子发生界面偏析时会与上表面争夺系统内部的溶质原子;3) 薄膜中的异质外延应力也会影响薄膜的偏析。因此,修正达肯模型的平衡态表达式不能直接应用于薄膜的表面偏析。为描述薄膜材料中的偏析,Wang在修正达肯模型的框架下,加入了对有限溶质原子数量的修正 [9]。Eugen等人在规则溶液模型框架下加入了有限膜层的修正,构建了规则溶液断键模型 [8]。该模型不仅可模拟任一厚度薄膜中的表面与界面偏析,而且考虑了溶质原子的扩散应力及膜层与衬底原子间的失配应力对偏析的影响,得到的结果与实验相吻合 [10]。修正达肯模型与规则溶液断键模型都是基于规则溶液近似发展而来,通过比较两个模型,可将宏观的热力学参数与微观的原子间相互作用参数建立起直接的关联,最终建立一个应用范围更广、能定量描述平衡态与动态偏析的模型是本论文的目的。本文将以Cu-Al超薄合金薄膜为例,对比基于宏观热力学参数的修正达肯模型与基于微观原子间相互作用参数的规则溶液断键模型的计算结果,分析了薄膜原子间相互作用系数、薄膜原子与衬底原子间相互作用以及应力对偏析的影响。
2. 模型
2.1. 修正达肯模型(Modified-Darken Model)
修正达肯模型把晶体分成N + 1层,每一层的厚度为d,如图1所示,并假设 [11]:
1) 系统为表面和体相组成的封闭系统;
2) 表面区域有限而体相无限;
3) 原子可以在表相和体相之间交换,以达到体系能量最小。
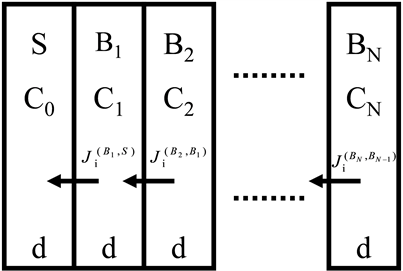
Figure 1. The crystal is divided into N + 1 layers (0 is the surface layer and N body layer)
图1. 晶体被分成N + 1层(0为表面层和N体层)
其中S为表面,B为体层。Ci为第i层溶质原子的浓度(C0为表面浓度),J为通量,d为层间距。体系中每一层的浓度随时间的变化由如下一组偶合速率方程描述:
(2-1)
D是偏析原子的扩散系数,R是气体常数,T为温度,
。
根据规则溶液近似,对二元系统,组元A (溶液原子)或B (溶质原子)的化学势
可表示为:
(2-2)
(2-3)
其中
为两种组元的相互作用系数。把(2-2)和(2-3)式代入偏微分方程组(2-1)中,可得第一个偏微分方程为:
(2-4)
其中,
,为第一体层和表面层化学势之差。当体系达到平衡状态时,偏析浓度不再随着时间变化,偏微分方程组(2-1)的值为零。式子(2-4)变形为:
(2-5)
表面偏析在薄膜材料中不同于块体材料。对于体块材料来说,偏析到表面层原子对“无限大”体层原子数量的影响很小,可以忽略不计,但对薄膜材料而言,表面偏析的原子数可能占系统总原子数的相当一部分,当体层的溶质原子偏析到表面后同时也严重改变了此原子在体内浓度的分布。即:
(C0、CN分别为薄膜上下表面) (2-6)
2.2. 规则溶液断键模型(Regular solution broken bond-type model)
如图2所示,规则溶液断键模型也是在规则溶液近似条件下,从微观的角度出发,将系统的总能量用原子间相互作用能表示,且考虑了系统的尺寸、膜层间以及膜层与衬底间相互作用、扩散应力以及异质外延应力对偏析的影响,用于定量描述合金薄膜体系表面/界面平衡态偏析 [8]。

Figure 2. A single crystalline thin film that is composed of A (matrix, blue) and B (solute, red) atoms is attached to a foreign substrate. The interface and interlayer coordination numbers are Z0 and Z1, respectively. EsA and EsB are the interaction energy of atoms A and B with the substrate, respectively
图2. 由溶液原子A (蓝色)和溶质原子B (红色)组成的单晶薄膜附着在衬底上。单晶薄膜分成N + 1层,其中N为表面层,0为界面层。Z0和Z1分别表示层内和层间的配位数。EsA和EsB分别表示A、B原子与衬底原子之间的键能
系统的总能量由内部化学能Ech、应变能Estress和系统的熵共同决定 [12]:
(2-7)
根据规则溶液近似,体系化学能可以用原子间的相互作用能表示为:
(2-8)
其中
为原子间的相互作用能,由原子间的键能EAA、EBB和EAB决定。EsA和EsB分别为A原子、B原子与衬底原子之间的键能,由原子与衬底的附着能Wad决定。
(2-9)
沉积在外来衬底上的薄膜会受到异质外延应力的作用,其应变能的贡献可表示为 [13]:
(2-10)
和V分别为薄膜的双轴弹性模量和原子体积。
为初始的双轴弹性应变,与薄膜的浓度无关。
为合金薄膜线性膨胀的单位变化量,由粒子的晶格常数决定 [14]。
最后,系统的熵可以表示为:
(2-11)
k为玻尔兹曼常数。
3. 修正达肯模型与规则溶液断键模型的比较
将规则溶液断键模型应用到沉积在蓝宝石衬底上的Cu(111)-5at%Al合金超薄膜体系,对于(111)取向的面心立方晶体来说,Z0 = 6,Z1 = 3,纯元素之间的键能和Cu-Al之间的键能可由下式得到 [15],其中A代表Cu,B代表Al。
;
(3-1)
(3-2)
和a分别表示纯元素的表面能和晶格常数。
为A、B原子之间的相互作用系数。
其它相关的参数通过下式计算:
; (3-3)
(3-4)
模拟计算所用参数列于表1与表2。

Table 1. Parameters for the Cu-Al alloy
表1. Cu-Al合金相关常数

Table 2. Parameters of Cu(A) and Al(B)
表2. Cu(A)、Al(B)纯元素相关参数
修正达肯模型与规则溶液断键模型都是建立在规则溶液近似的框架下,不同的是修正达肯模型的提出开始是针对块体系统,而在薄膜体系中溶质原子的储存能力有限,所以用修正达肯模型描述薄膜材料偏析时,还需要做进一步的修正 [19]。修正达肯模型最突出的特点是既可以描述平衡态偏析又可以描述动态偏析。规则溶液断键模型的提出主要针对有应力存在的薄膜体系,特别考虑了薄膜与衬底原子间失配应力以及扩散应力对偏析的影响,但仅描述平衡态偏析。
对于上坡扩散的偏析,现已普遍认为偏析的驱动力是化学势梯度,即修正达肯模型中的偏析能
,其值可以通过拟合测量的偏析实验数据获得,也可以通过相图计算或者Miedema半经验公式估算 [20]。根据偏析能的定义,其亦可用微观原子间相互作用能表示,
表示表面偏析能 [8]:
(3-5)
同理,界面偏析能
可以表示为 [8]:
(3-6)
修正达肯模型中除偏析能外,另一个宏观热力学参数是原子间相互作用系数
,该系数与规则溶液断键模型中每对原子之间的相互作用系数
的关系如下 [20] [21] [22]:
(3-7)
下面将以温度为700 K时,不同Al体浓度的Cu-Al合金薄膜为例,比较两种模型的平衡态偏析结果。体浓度选取在Cu-Al相图中Cu(Al)固相共溶体区,三个具体的Al体浓度分别为1at%,10at%和20at%Al。
首先用自由薄膜的平衡态偏析,即先不考虑应力的影响。T = 700 K时,利用Miedema模型 [20] 计算得到
,
[23]。利用式子(3-5)和(3-7)得:
,
。如图3可得,在考虑相同条件的情况下,当两个模型的相互作用系数和偏析能一样时,模拟出的结果相差不大。Al浓度分别为1at%,10at%和20at%时,两模型计算结果的相对误差分别为0.19at%,1.03at%和4.45at%。修正达肯模型的计算结果稍大一些,出现差异的原因可能有:第一,因为计算方式不同带来的误差;修正达肯模型使用解耦合的偏微分方程组,规则溶液断键模型使用坐标下降法计算;第二,计算精度的影响;第三:模型差异带来的不同(详见下文)。
根据二元体系规则溶液化学势的定义可得:
(3-8)
(3-9)

Figure 3. Al equilibrium layer concentrations for the Cu-Al alloy free-standing film (N = 9) with three bulk concentrations of 1at%, 10at% and 20at% Al at 700 K, as D for the modified Darken model and R for the regular solution broken bond-type model
图3. T = 700 K时,Cu-Al自由薄膜到达平衡态时Al在每一层的浓度分数(N = 9)。R表示用规则溶液断键模型计算得到,D表示用修正达肯模型计算得到。Cu-Al薄膜中Al的浓度分别为1at%、10at%和20at%
将式(2-12)分成两部分,第一项表示异质外延应力,第二项表示扩散应力:
(3-10)
按(3-8)和(3-9)分别对扩散应力求偏导得:
(3-11)
(3-12)
(3-13)
(3-14)
其中
和
分别表示溶液原子(Cu)在表面层和体层中由于弹性能产生的化学势。
和
分别表示溶质原子(Al)在表面层和体层中由于弹性能产生的化学势。将应力修正引入式(2-2)和(2-3)得:
(3-15)
(3-16)
将上式带入偏微分方程组(2-1)中,可得第一个偏微分方程为:
(3-17)
在考虑扩散应力影响后,修正达肯模型对自由薄膜偏析的模拟计算结果如图4所示。浓度为1at%,10at%和20at%Al时,两模型计算结果的相对误差分别为0.21at%,0.31at%和0.04at%。
图5给出了原子间相互作用对表面偏析影响的模拟计算结果,其中Al的浓度为5at%,当Ω = −7600,7600和30,000 KJ时,两模型计算结果的相对误差分别为0.44at%,0.68at%和0.70at%,即相互作用系数越大时,两个模型计算结果相差增加,但仍低于1%。由式子(3-2) (3-6)可知,原子间相互作用直接影响AB原子间的键能。由于系统中,溶质原子的掺杂比较小,绝大多数的Al都会与Cu形成Cu-Al键。当ω(Ω)增大时,Cu-Al键能增大,更多的Al往界面和表面偏析可以减少系统内的Cu-Al键,从而减少系统的总能量。当Cu-Al能较小时,且EsA比EsB小,此时Cu往界面的偏析更有利于降低系统总能量。也就是说,无论是在界面处还是表面处,增大ω(Ω)都有利于Al的偏析。利用键对模型计算时,系统到达平衡,体内层的浓度并不完全一致,靠近表面体层Al浓度比体内的Al浓度稍微偏大。从放大的图可以看到,Ω越大,N = 1和N = 8层的浓度与体内浓度差异越大。这是因为靠近表面的地方Al浓度大,Cu与Al更容易与表层的Al成键。当EAB的值较大时,Cu与Al形成Cu-Al键,不利于降低系统的总能量。所以,在靠近表面层处,Al浓度更高。类似的情况在Ni-Au体系中也存在 [8]。但对于达肯模型来说,体内每一层的化学势都一样,所以平衡时体内各层浓度保持一致。

Figure 4. Al equilibrium layer concentrations for the Cu-Al alloy free-standing film (introduced diffusion stress) with three bulk concentrations of 1at%, 10at% and 20at% Al at 700 K, as D for the modified Darken model and R for the regular solution broken bond-type model
图4. T = 700 K时,Cu-Al自由薄膜(考虑扩散应力)到达平衡态时Al在每一层的浓度分数。R表示用规则溶液断键模型计算得到,D表示用修正达肯模型计算得到。Cu-Al薄膜中Al的浓度分别为1at%、10at%和20at%
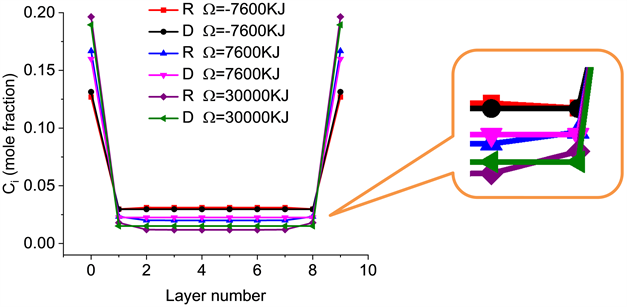
Figure 5. Al equilibrium layer concentrations for the Cu-Al alloy free-standing film (introduced diffusion stress) with Ω = −7600 KJ, 7600 KJ and 30,000 KJ at 700 K, as D for the modified Darken model and R for the regular solution broken bond-type model
图5. T = 700 K时,Cu-5at% Al自由薄膜(考虑扩散应力)到达平衡态时Al在每一层的浓度分数。R表示用规则溶液断键模型计算得到,D表示用修正达肯模型计算得到。Cu-Al薄膜中Ω分别为−7600 KJ,7600 KJ,30,000 KJ
接下来将界面偏析能引入到达肯模型中,以沉积在蓝宝石衬底上的Cu-Al薄膜为例,模拟700 K条件下薄膜的表面(N = 9)和界面(N = 0)的偏析。如图6所示,两模型计算结果几乎相同,表面处Al的平衡态偏析浓度高于界面处。

Figure 6. Al equilibrium layer concentrations for the Cu-Al alloy film deposited on the sapphire substrate with three bulk concentrations of 1at%, 10at% and 20at% Al at 700 K, as D for the modified Darken model and R for the regular solution broken bond-type model
图6. T = 700 K时,蓝宝石衬底上的Cu-Al到达平衡态时Al在每一层的浓度分数。R表示用规则溶液断键模型计算,D表示用修正达肯模型计算。Cu-Al薄膜中Al的浓度分数分别为1at%,10at%,20at%
最后将异质外延应力分别引入表面和界面偏析能中 [8]:
(3-18)
(3-19)
如图7所示,我们考虑了表面(
)和界面(
)不同于体层(
)的情况。两模型计算结果相差最大为1at%左右,造成误差的原因除了上文中提到的因素之外,还有添加多个修正时误差累加的结果。如图7(a)和图7(c),当界面处发生晶格失配时,异质外延压应力将Al原子推向界面。当异质外延应力从压应力往拉应力变化时,界面处Al浓度降低并伴随着表面处Al浓度上升。对比图7(a)和图7(c)可得,晶格完全失配时放大了异质外延应力对偏析的影响。如图7(b)和图7(d),当表面发生晶格失配时,异质外延压应力将Al原子推向表面。

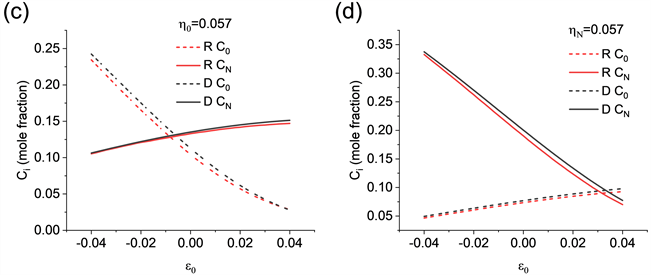
Figure 7. Al equilibrium surface (solid line)/interface (dash line) concentration as a function of the heteroepitaxial biaxial strain (ε0) at the temperature of 700 K with the relaxation of the solute atom size misfit (ƞ) on the surface, and at the interface, as D for the modified Darken model and R for the regular solution broken bond-type model
图7. T = 700 K时,在表面、界面处溶质原子晶格完全失配(ηN, η0 = 0)和部分弛豫(ηN, η0 = 0.057)情况下,改变异质外延应力(ε0),蓝宝石衬底上的Cu-5at%Al到达平衡态时Al在表面(实线)和界面(虚线)的浓度分数。R表示用规则溶液断键模型计算,D表示用修正达肯模型计算
4. 结论
1) 模拟计算表明:附着在蓝宝石衬底上的Cu-5at%Al薄膜,Cu在薄膜与衬底界面上偏析和Al在表面偏析,与实验吻合;
2) 当薄膜各层应变参数相等且为常数时,异质外延应变对表面和界面的偏析没有任何影响;
3) 当薄膜的表面或界面发生晶格失配时,异质外延压应力使Al往失配处偏析,当Cu、Al晶格完全失配时,更有利于Al的偏析;
4) 在修正达肯模型中引入弹性能产生的化学势,就可以模拟扩散应力对偏析的影响,使得修正达肯模型的应用范围更为广泛。
基金项目
本工作获得汕头大学启动资金项目(No. NTF18021)、光学与光电子工程项目(No. 2018KCXTD011)和广东大学重点平台项目(No. 2021GCZX009)的资助。
NOTES
*通讯作者。