扇形算子情形下时滞发展方程周期解的存在性
Existence of Periodic Solutions for Delayed Evolution Equation with Sector Operator
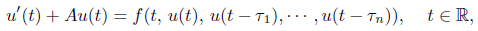
摘要: 本文讨论了Banach 空间X中时滞发展方程周期解的存在性，其中A:D(A)⊂X→X为扇形算子，−A生成X中指数稳定的解析半群T(t)(t≥0),f:ℝ×Xn+1→X连续，关于t以ω为周期，τ1, •••,τn > 0。我们应用不动点定理，获得了方程ω-周期mild 解的存在性结果。
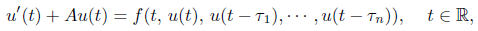
Abstract: This paper deals with the existence of periodic solutions for delayed evolution equation in a Banach space X, where A:D(A)⊂X→X is a sector operator and −A generates a exponential stability analytic semigroup T(t)(t≥0),f:ℝ×Xn+1→X is a continuous function mapping and it is ω-periodic in τ1, •••,τn > 0. Existence results of ω-periodic mild solutions are obtained by using the fixed point theorem.
文章引用：韦启林. 扇形算子情形下时滞发展方程周期解的存在性[J]. 理论数学, 2022, 12(4): 653-664. https://doi.org/10.12677/PM.2022.124075

参考文献

[1] Hale, J. and Lunel, S. (1993) Introduction to Functional Differential Equations. Springer- Verlag, Berlin.
https://doi.org/10.1007/978-1-4612-4342-7 1
[2] Wu, J. (1996) Theory and Application of Partial Functional Differential Equations. Springer- Verlag, New York.
[3] Vejvoda, O. (1982) Partial Differential Equations: Time-Periodic Solutions. Martinus Nijhoff Publishers, Boston.
https://doi.org/10.1007/978-94-009-7672-6
[4] 杨和. 扇形算子发展方程的周期解及渐近性态[D]: [硕士学位论文]. 兰州: 西北师范大学, 2008.
[5] Liu, J. (1998) Bounded and Periodic Solutions of Finite Delay Evolution Equations. Nonlinear Analysis, 34, 101-111.
https://doi.org/10.1016/S0362-546X(97)00606-8
[6] Li, Y. (2011) Existence and Asymptotic Stability of Periodic Solution for Evolution Equations with Delays. Journal of Functional Analysis, 261, 1309-1324.
https://doi.org/10.1016/j.jfa.2011.05.001
[7] Li, Q. (2018) Monotone Iterative Technique for Delayed Evolution Equation Periodic Problems in Banach Spaces. Pure and Applied Mathematics Quarterly, 14, 393-417.
https://doi.org/10.4310/PAMQ.2018.v14.n2.a4
[8] Li, Q. and Li, Y. (2021) Positive Periodic Solutions for Abstract Evolution Equations with Delay. Positivity, 25, 379-397.
https://doi.org/10.1007/s11117-020-00768-4
[9] 李强. 时滞发展方程周期mild解的存在性[J]. 山西大学学报(自然科学版), 2018, 41(2): 287-294.
[10] Pazy, A. (1983) Semigroups of Linear Operators and Applications to Partial Differential E- quations. Springer-Verlag, Berlin.
[11] 李永祥. 散度抛物型变分边值问题的周期解[J]. 应用数学, 1994, 7(3): 287-293.
[12] 郭大钧. 非线性分析中的半序方法[M]. 济南: 山东科学技术出版社, 2000.
[13] 夏道行, 严绍宗. 实变函数与应用泛函分析基础[M]. 上海: 上海科学技术出版社, 1987. [14] 郭大钧. 非线性泛函分析[M]. 第3版. 北京: 高等教育出版社, 2015.

为你推荐