基于超声波的液面位置测量方法研究

Research on Liquid Level Position Measurement Method Based on Ultrasonic Wave

摘要: 本文提出了基于超声波在浸液波导杆中的传播测量液面位置的方法。建立超声波在浸液波导杆和空气波导杆传播的模型。通过超声波在波导杆中的纵波到达时刻以及传播距离分别计算了空气波导杆和浸液波导杆中纵波的传播速度。根据超声波在空气波导杆和浸液波导杆底部到达的时间差，结合超声波速度，推导出计算液面的理论公式，估算液面位置。

Abstract: This paper presents a method to measure the liquid level position of fuel machine based on the propagation of ultrasonic waves in immersion waveguide rod. The model of ultrasonic wave propagation in submerged waveguide rod and air waveguide rod is established by method. The propagation velocity of longitudinal wave in air waveguide and submerged waveguide was calculated by the arrival time and propagation distance of ultrasonic wave. Based on different arriving time between ultrasonic waves at the bottom of the air waveguide rod and the immersion waveguide rod, the theoretical equation for calculating the liquid level is derived by combining the ultrasonic wave velocity. According to the time difference between the ultrasonic wave arrival at the bottom of the air waveguide rod and the submerged waveguide rod, combined with the ultrasonic speed, the theoretical formula for calculating the liquid level is derived to estimate the liquid level position.

1. 引言

为了检测流体容量，特别是针对为了适应高度变的越来越浅，且几何形状愈加复杂的容器，以实现可靠的安全性和对污染的抵抗力，便有了许多种方法测量液位。其中包括两大类：第一类是接触式，第二类是非接触式 [1]。接触式是较为传统的测量方法，其中包括手动式、浮子式、磁致伸缩式、伺服式和电容式等。缺点是耗时耗力，不能适用于强腐蚀性或者有毒液体 [2]，零件易磨损，结构复杂且不能实现实时检测 [3] [4]。优点是方式理论简单，容易实现且成本极低，能应用于温度压力较高的液体环境。非接触测量法有以下几种：雷达测距方法、超声波测距方法、激光测距方法、红外测距方法等 [5]。红外测量是通过红外线的物理特性测量的，其特点是便宜、简单，但是缺点也显而易见，红外线非常容易被温度影响而且难以精确检测。激光测量的优点是精度高，操作简单，但受到环境因素制约大，成本极高且维护系统非常复杂 [6]。雷达测量具有精度高的优点，但缺点是电路复杂且成本高。

超声波适用于各种磁场或者光强度高的环境，不仅可以用于检测难以反射的物体，而且可用于无光、多尘、电磁干扰较强的环境 [7] [8] [9] [10]；基于上述优点，这种测量方式在各类工程领域和生产中越来越受到重视 [11] [12]。由于液体的粘滞特性，超声波在浸液波导铝杆传播的速度将产生变化。因此，本文提出通过接收的超声信号的直达波、液面反射回波和波导杆底部反射回波到达时刻，结合空气波导杆中传播的速度和浸液波导杆中声波速度，计算了液面的位置。该方法为容器液面位置测量提供了理论的指导。

2. 理论模型

当超声波在波导杆中传播到不同介质的分界面时，部分能量被反弹，通过检测超声波的直达波和接收到的反射波之间的时间差来计算激励源位置到反射面的距离 [7]。

本文中将长度为S的波导杆垂直放置，直接加固在容器底部，其模型如图1所示。建立高为20 mm，宽为10 mm的二维矩形作为波导杆，以A1表示，其材料为铝，材料参数如表1所示。建立两个高为8 mm，宽为10 mm的二维矩形，分别以A2、A3表示液体。激励源作用于如图1所示位置，其位移公式为

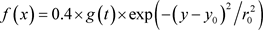(1)

其中，y₀表示超声激励源位置，r₀为激励源宽度，g(t)表示激励源的时间分布，其表达式为

$g\left(t\right)=\frac{t}{t^{\prime }}\exp \left(\frac{-t}{t^{\prime }}\right)$ (2)

其中，t'表示超声激励源作用时间

Figure 1. Fuel machine liquid level measurement model

图1. 燃油机液面测量模型

Table 1. Parameters of aluminum materials

表1. 铝材料的参数

超声换能器激发产生的超声导波沿着波导杆传播，在空气和液体的交界发生反射和透射，反射波被超声换能器接收，而透射波将会在液体波导杆中继续传播，直达波导杆底部，被信号接收器接收。波导杆中传播的导波包含横波和纵波模态。由于纵波信号强，且其反射波和透射波受到的干扰小，因此，本次的测量采用纵波。由接收器接受到的纵波在浸液的波导杆中传播的时间减去纵波在空气波导杆中传播的时间便可以得出时间差t₀

$t_0=t_2-t_1$ (3)

其中，t₁为无液浸模型下纵波的传播时间，即空气波导杆中的传播时间；t₂为液浸模型下的纵波传播时间，既包含空气波导杆中传播的，也包含液体波导杆中传播的。

假设L为激励源位置，在此取L = 10 mm，X为液面位置，如图1所示，V_air为空气波导杆中纵波的

速度，V_liquid为液体波导杆中纵波的速度。无液浸模型，其底部信号接收器接收的到纵波到达时刻t₂为 $\frac{L}{V_{air}}$ ；液浸模型，其底部信号接收器接收的到纵波到达时刻t₁为 $\frac{X}{V_{liquid}}+\frac{L-X}{V_{air}}$，由此可以列出方程

$t_0=\frac{X}{V_{liquid}}+\frac{L-X}{V_{air}}-\frac{L}{V_{air}}$ (4)

由此得到液面位置为

$X=\frac{t_0\times V_{air}\times V_{liquid}}{V_{air}-V_{liquid}}$ (5)

由此可以得到液面位置的测量与激励源位置无关。

为了满足超声波传播精度的要求，网格单元的尺寸选择5 μm。时间步长的选择可以决定计算结果中结构响应中最高频率和解的精确度，在此时间步长取值为2 ns，总计算时间t取值为5 μs。

3. 结果与讨论

超声波在铝板内部的速度约6000 m/s~6200 m/s，而横波在铝板内部的速度约3000 m/s~3100 m/s，加入激励源信号后，将产生纵波和横波，且纵波的速度是远大于横波的，因此在激励之后将检测出两列波阵面。图2分别是无浸液和浸液模型在1 μs时的波形图，途中观察出来了两列波阵面，速度最快的是纵波，速度慢的是横波。浸液模式下，图2(b)观察到泄露到液体中传播的声波。但是此图不能明显区分液体对声波速度的影响。

(a) (b)

Figure 2. Displacement field diagrams at 1 μs for the no-liquid immersion model (a) and the immersion model (b)

图2. 无液浸模型(a)和浸液模型(b) 在1 μs时位移场图

将整个波导杆置于空气中，距离预设液面为3 mm~6 mm处，间隔1mm，取4个点，其时域波形如图3所示。通过观察波形可以发现随着距离激励源位置的增大，其位移波形出现的越来越晚。在距离液面3 mm处纵波的位移时间为0.935 μs，距离液面4 mm处纵波的位移时间为1.105 μs，距离液面5 mm处纵波的位移时间为1.275 μs，距离液面6 mm处纵波的位移时间为1.45 μs，由最小二乘法拟合得到的直线斜率为纵波在空气中的传播速度，约为5848 m/s。在距离液面5 mm处和6 mm处，发现了在纵波和横波之间出现了一个较为明显的位移。纵波传播到波导杆底部产生反射波，为回波法测液位提供了条件。

当波导杆浸入液体时，距离预设液面为3 mm~6 mm处，间隔1 mm，取4个点，其时域波形如图4所示。观察波形可以发现随着距离激励源位置的增大，其位移波形并没有发生明显的衰减，但是其位移振幅是无液浸模型的一半，这是由于液体负载加大了波振动的阻力。在距离液面3 mm处纵波的位移时间为0.96 μs，距离液面4 mm处纵波的位移时间为1.155 μs，距离液面5 mm处纵波的位移时间为1.345 μs，距离液面6 mm处纵波的位移时间为1.535 μs，由最小二乘法可以计算出纵波在有液体负载的波导杆中传播速度为5263 m/s，小于空气波导杆中纵波的速度。

Figure 3. Point-by-point displacement diagram of the model without liquid immersion

图3. 无液浸模型逐点位移图

Figure 4. Point-by-point displacement diagram with liquid immersion model

图4. 有液浸模型逐点位移图

与无液浸模型相比，浸液波导杆中横波波形振幅并不十分突出。图中4 μs左右，观察到比较强的波的振幅，其幅度大于横波振幅。根据物理模型中波形传播的时间和距离测算，发现这个振幅为纵波的反射波。横波由于速度慢，反射波到达时刻较长，回波干扰信号多，因此本文中液面计算采用纵波。

波导杆底部位移的时域波形图便是接收器接收到的超声信号。超声信号从激励源产生到被接收器接受，经历了无浸液波导杆和浸液波导杆两部分的传播。图5是浸液和无浸液两种模型下波导杆底部接收到的超声波位移图。从图中可观察到液浸模型和无浸液模型下的纵波到达时刻分别为1.915 μs和1.765 μs。将前文研究得出的参数V_liquid = 5263 m/s和V_air = 5848 m/s，带入公式(5)，可以得出液面位置X为7.89 mm，而检测的实际的液位为8 mm，产生的误差约为0.11 mm，误差为1.4%，由此可确定此方法可进行液面位置的测量。

Figure 5. Waveform displacement diagram at the bottom of the waveguide rod

图5. 波导杆底部的波形位移图

4. 结论

本文阐述了超声波在空气波导杆和浸液波导杆中的传播特性，从而确定了测量容器液位的方法。首先，根据超声波在空气波导杆和浸液波导杆中传播速度不同，给出了计算液面位置的理论公式。其次，发现液面位置的测量与空气波导杆中超声波的速度、浸液波导杆中超声波的速度以及到达波导杆底部的时间差有关。最后，分别建立了超声波在空气波导杆和浸液波导杆传播的模型。距离预设液面为3 mm~6 mm处，间隔1 mm，取4个点，分别得到超声波在空气波导杆和浸液波导杆两种情况传播的波形图。根据纵波到达时刻和距离预设液面的长度，计算得到了空气波导杆中传播的纵波速度为5848 m/s，浸液波导杆中传播的纵波速度为5263 m/s。波导杆底部接收了两种情况下的超声波，从而得到了声波传播的时间差。将上述参数带入理论公式，可以得出液面位置X为7.89 mm，检测的实际的液位为8 mm，产生的误差约为0.11 mm。该方法为测量容器中液体液面位置提供了理论指导。