1. 引言
聚类是将样本按其自身的属性聚成若干类,以保证类内样本相似度尽可能高,而类间样本相似度尽可能低。经典的聚类方法有K-Means [1] 和K-Medoids [2]。Qian等 [3] 从聚类标准、聚类表示及算法框架角度分析了多个流行的聚类算法,该文在国内聚类算法领域具有一定的地位。Johannes等 [4] 从数据挖掘的角度分析了一些聚类方法。Hoppner等 [5] 提出了模糊聚类的方法,基于模糊集中隶属度以及数据区间隶属度来划分不同类,姚一豫等 [6] 用区间集表示聚类结果中的一个类,通过离散化数据集刻画类差异性以及类间相似性。这些都是传统的二支聚类,样本要么属于这个类,要么不属于这个类,聚类具有清晰的边界,这样会造成很大的误分类。
针对上述问题,本文首先对高维数据通过主成分分析方法进行降维,有效地处理了目前大规模高维数据集,并将粗糙集与聚类相结合,将聚类划分为三个不相交的区域,将不确定性的对象划分到边界域中,提高聚类的准确率。最后,本文选取了陕西省内11个城市的25个经济指标进行研究。根据这些经济指标将11个城市进行粗糙聚类。通过对经济指标的研究分析,得到陕西省各地区城市发展现状,为今后各城市经济发展提供一些依据。
2. 基本概念
2.1. 主成分分析
主成分分析 [7] [8] [9] (Principal Component Analysis,简称PCA)就是考虑各指标之间的相互关系,利用降维的方法将多个指标转换为少数几个互不相关的指标,从而使进一步研究变得简单的一种统计方法。主成分分析是1933年首先提出的一种“降维”的思想,在损失很少信息的前提下把多个指标转化为几个综合指标,称为主成分。主成分分析主要是使用降维的方法,使用较少的变量来代替原有的较多的变量。在变量转换过程中,采用了映射的原理。即较少的变量是原有较多属性变量的线性表示。具体内容如下:
假设原来的变量指标为
,它们的综合指标,即新变量指标为
,则
(1)
其中,
即为数据集的主成分,是原来变量指标的线性表示。
是系数矩阵。主成分和原始变量之间的关系是通过系数矩阵来体现的。主成分满足互不相关的要求,这在线性数学中满足逆矩阵相乘的条件。否则,则求不出系数矩阵。
是
的线性组合中的方差最大指标;
是与
不相关的
的线性组合中的方差最大指标。依此类推,
是
都不相关的
的所有线性组合中的方差最大指标。这就使得主成分指标比原始指标具有某些更优越的性能。主成分分析不能看作是研究的结果,而应该在主成分分析的基础上继续采用其他方法解决问题。
2.2. 粗糙集
粗糙集(Rough Set) [10] [11] 是波兰数学家Pawlak在1982年首先提出的一种处理不确定、不精确性知识的数学方法。粗糙集作为一种较新的软计算方法,近年来越来越受到重视,其有效性已在许多科学与工程领域的成功应用中得到证实,是当前国际上人工智能理论及其应用领域中的研究热点之一。在粗糙集中,近似集理论是非常重要的一部分,通过近似集理论确定目标集的上、下近似,计算目标集的边界域及负域,并刻画出那些不确定的知识的粗糙程度。
定义1 [12] [13] 设信息系统是一个四元组
。U是非空有限的对象集合,At是属性集
合,
是属性值的集合,
属性a的值域,f是信息函数,且对任意
,
,
。
定义2 [12] [13] 给定信息系统
。对于每一个属性子集
,等价关系
定义如下:
. (2)
是论域U上的划分,
表示论域U中对象x关于等价关系
的等价类,为U中基于属性子集A的确定性知识。为方便表现,信息系统
简记为
,
简记为
,
简记为
。
例1表1给出信息系统
,其中
,
。
在表1中,属性集At产生的等价类为:
属性子集
产生的等价类为:
属性子集
产生的等价类为:
定义3 [12] [13] 给定信息系统
。对任意
,
,目标集X关于属性子集A的上近似
和下近似
分别定义为:
(3)
一般地,基于属性子集A和目标集X,可得目标集X与下近似的关系:
,即下近似
中的元素完全属于目标集X。同样可得目标集X与上近似的关系:
,即目标集X中的元素一定属于上近似
。
对于目标集
,若
,则目标集X称为可定义集;若
,则目标集X称为粗糙集。如果给定属性子集A和目标集X,论域U被划分为如下三个不相交的区域 [14]:
1)
,称为目标集X关于属性子集A的正域;
2)
,称为目标集X关于属性子集A的边界域;
3)
,称为目标集X关于属性子集A的负域。
因此,基于属性子集A和目标集X,论域U被划分为三个不相交的区域,如图1所示。
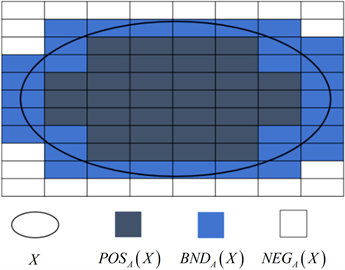
Figure 1. Three disjoint regions based on Pawlak rough set
图1. 基于Pawlak粗糙集的三个不相交区域
2.3. 聚类分析
K-Means算法最早由Steinhaus,Lloyd和MacQueen于20世纪五六十年代在不同的科学领域独立发现的 [1],是典型的基于距离的聚类算法之一。它采用距离作为相似性的评价指标,即认为两个样本的距离越近,其相似度就越大 [15]。具体算法见表2:
计算所有距离的算法复杂度为
,因此算法1的复杂度为
。
3. 基于粗糙集的主成分聚类及实证分析
3.1. 基于粗糙集的主成分聚类
本节将粗糙集中的下、上近似与K-Means聚类相结合,将聚类中心改为:
(4)
其中,e表示权重,upper表示粗糙集的上近似集,lower表示粗糙集的下近似集。
和
分别表示第i个类的下近似集和上近似集的样本个数。本文运用一种基于主成分分析的粗糙集聚类算法。即对数据先进行主成分分析,然后进行粗糙集聚类,得到聚类中心,每个类都包含有上近似集和下近似集,下近似集中的对象表示确定属于该类的对象,上近似集的对象表示可能属于该类的对象。基于粗糙集的主成分聚类分析算法如表3:

Table 3. Principal component clustering algorithm based on rough set
表3. 基于粗糙集的主成分聚类算法
计算所有距离的算法复杂度为
,因此算法2的复杂度为
。
3.2. 实验结果及分析
3.2.1. 数据集
本文研究的数据是陕西11个城市的25个经济指标数据。数据来源于由国家统计局主编的《陕西统计年鉴》第二部分。陕西省的11个城市分别为:西安市、铜川市、宝鸡市、咸阳市、渭南市、杨凌示范区、汉中市、安康市、商洛市、延安市、榆林市。25个经济指标为:年底常住人、城镇非私营单位就业人员年末人数、生产总值、房地开发投资、地方一般性支出、一般预算支出、城镇非私营单位就业人员工资总额、城镇非私营单位就业人员平均工资、城镇居民均可支配收入、农村居民人均可支配收入、农林牧渔业总产值、粮食产量、棉花产量、油料产量、规模以上工业总产值、邮电业务总量、固定电话、移动电话、社会消费品零售总额、进出口总值、出口总值、实际利用外直接投资额、卫生机构数、卫生机构床位数、卫生技术人员。如表4所示。

Table 4. The basic descriptions of data sets
表4. 数据基本描述
3.2.2. 实验结果
1) 传统聚类分析
a) 使用SPSS进行的数据分析,得出初始聚类中心见表5。

Table 5. Initial cluster center table
表5. 初始聚类中心表
b) 表6为迭代历史,该表给出了迭代过程中类中心的变动量,可以看出本次聚类过程进行了2次就收敛了。
c) 表7为聚类成员,该表给出了样本观测量所属类别以及与所属类中心的距离。从表7中可以看出,将11个城市分成了3类,{西安}为第一类,{铜川市、杨凌示范区、安康市、商洛市、延安市}为第二类,{宝鸡市、咸阳市、渭南市、榆林市、汉中市}为第三类。
由于以上部分的分析都是在表中展示了聚类中心之间的距离以及各类城市的聚类类别,数据可视性较差。图2是本文根据K-Means聚类方法在R语言上绘制聚类成像图,使得各聚类成员所属类别以及各类别之间的距离更为清楚和可视化。

Figure 2. Clustering member based on K-means
图2. 基于K-means聚类成员图
2) 主成分聚类分析
由经典聚类分析的聚类结果得到:25个属性代表11个城市的经济指标,数据信息冗余量较大,而且很多信息在计算过程中对计算结果带来了干扰。所以需要先进行主成分分析以达到降维的目的。
这一部分利用主成分分析的结果作为聚类分析的数据源,对数据进行基于粗糙集的聚类分析。将这11个城市(示范区)进行基于粗糙集的聚类分析,得到最终的聚类中心和聚类的上近似集和下近似集中心。如表8所示:
根据聚类的上近似集中心和下近似集中心,可以的得到基于主成分降维后的粗糙集聚类结果如表9所示:

Table 9. Number of objects in the cluster
表9. 聚类中的对象个数
根据聚类的上、下近似集的聚类结果可得基于粗糙近似集的主成分聚类结果,如表10所示:

Table 10. Principal component clustering results based on rough approximation set
表10. 基于粗糙近似集的主成分聚类结果
图3根据基于粗糙近似集的主成分聚类方法在R语言上绘制聚类成像图,使得各聚类成员所属类别以及各类别之间的距离更为清楚和可视化。
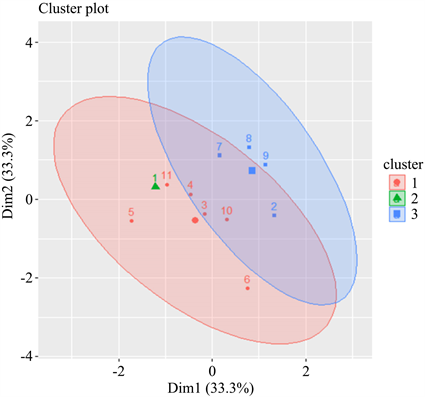
Figure 3. Principal component clustering member based on rough approximation set
图3. 基于粗糙近似集的主成分聚类成员图
4. 总结
本文提出了基于粗糙集的主成分聚类方法。首先通过主成分分析将高维数据降维,解决了高维数据难处理的问题。进一步将粗糙集与聚类相结合,将数据集划分为不相交的三部分,降低了误分类的概率。最后对陕西11个城市的25个经济指标数据进行实验,将11个城市划分为三类,{西安}为第一类,{汉中市、安康市、商洛市、延安市}为第二类,{宝鸡市、咸阳市、渭南市、榆林市}为第三类。但从聚类的结果中可以看到存在一定的不合理性。例如,咸阳市毗邻西安市,实际的经济水平高于其他城市。在基于粗糙集的主成分聚类结果中,将11个城市划分为三类,第一类仍然为西安,陕西省省会城市经济发展水平远高于其他城市。第二类为中等发展城市,第三类为不发达城市。采用本文方法得到的聚类结果更为合理,层次更为鲜明,同时也与实际情况较为契合。