1. 引言
本文讨论的都是有限无向,无自环和重边的图。
对于一个非空图
,我们用
,
,
和
分别表示它的顶点集、边集、弧集和全自同构群,记
和
分别为图
的阶和度数。给定顶点
,与顶点
邻接的点集称为
的邻域,记为
,
称为点
的度数。我们称顶点集的一个
序列
为
的一条s-弧,如果任意相邻两点邻接且
,其中
。设
,若G在
、
、
上的作用传递,则分别称
为G-点传递图、G-边传递图和G-弧传递图。
边本原图是弧传递图 [1] 的一个特殊子类,因此其具有特殊性但不失普遍性。我们知道除了星图外边本原图都是弧传递图,因此我们称一个边本原图是非平凡的,如果其是连通的弧传递图并且其度数至少是3。相比于弧传递图,边本原图的例子十分稀少,因此刻画边本原图是一项有意义的工作。
许多著名的图都是边本原的。如著名群论学家Weiss [2] 于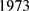 年对3度边本原图的完全分类,其中有6阶的完全二部图,14阶的Heawood图,30阶的Tutte-Coxeter图以及102阶的Biggs-Smith图。约30年后,Li等人重新开始对边本原图的研究工作。如M. Giudici和Li [3] 于2010年系统地分析了边本原图可能的点作用和边作用,并且决定了基柱为
的G-边本原图。Li和Zhang [4] 于2011年决定了边本原s-弧传递图的分类(
)。Feng,Li和Guo [5] [6] 于2011年分别决定了度数为4和5的边本原图。Pan和Wu [7] 于2017年刻画了6度的边本原图,并且完全分类了边稳定子群为可解的情形。此外,近几年,对具有特定阶的边本原图的研究取得了创新性的成果。如Pan和Wu [8] [9] 于
年对3度边本原图的完全分类,其中有6阶的完全二部图,14阶的Heawood图,30阶的Tutte-Coxeter图以及102阶的Biggs-Smith图。约30年后,Li等人重新开始对边本原图的研究工作。如M. Giudici和Li [3] 于2010年系统地分析了边本原图可能的点作用和边作用,并且决定了基柱为
的G-边本原图。Li和Zhang [4] 于2011年决定了边本原s-弧传递图的分类(
)。Feng,Li和Guo [5] [6] 于2011年分别决定了度数为4和5的边本原图。Pan和Wu [7] 于2017年刻画了6度的边本原图,并且完全分类了边稳定子群为可解的情形。此外,近几年,对具有特定阶的边本原图的研究取得了创新性的成果。如Pan和Wu [8] [9] 于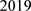 年完全分类阶为素数幂和二倍素数幂的边本原图。在此基础上,我们研究的一个目的是去寻找具有其他特定阶的边本原图例,因此本文的主要内容是刻画阶为三的次幂倍奇素数幂的边本原图。
年完全分类阶为素数幂和二倍素数幂的边本原图。在此基础上,我们研究的一个目的是去寻找具有其他特定阶的边本原图例,因此本文的主要内容是刻画阶为三的次幂倍奇素数幂的边本原图。
本文所使用的符号都是标准的。如Atlas [10],我们有时用正整数n来表示n阶循环群
。对于一个素数幂
,用
表示q阶的初等交换群。其他有限群符号可参考 [11]。对于两个群N和H,我们用
表示N和H的直积,用
表示N被H扩张,如果这个扩张是可裂的,则记为
。用
和
分别表示为群T的全自同构群和外自同构群。用
表示阶为a且度数为b的G-边本原图。下面是本文的主要结果。
定理1.1 设
是阶为
的G-边本原图,其中a和b为正整数,p为奇素数且
。如果G在
上本原,
。则图
可能是表1所列的其中一种情形。
本文的结构如下:在第二节,给出群论和图论中的相关定义和引理。在第三节,给出定理1.1中图例的证明。

Table 1. Edge-primitive graphs of order 3 a p b
表1. 阶为
的边本原图
2. 预备知识
下面首先给出有限群论中的一个经典结论。
引理2.1 [12] 设p和q是素数,a和b是正整数,那么阶为
的群是可解群。
考虑群在集合上的作用,我们给出秩和次轨道的定义。
定义2.2 [13] 设G是集合Ω上的置换群,对任意的
,我们称点
的稳定子群
在
上的轨道为G的一个次轨道。G的次轨道个数称为G的秩。当次轨道的长度大于1时,我们称这是G的非平凡次轨道。
我们判断G在集合Ω上是否本原,常通过下面的引理进行判断。
引理2.3 设G在集合Ω上传递,对任意的
,则G在Ω上本原当且仅当点
的稳定子群
是G的极大子群。
本原置换群的分类在 [14] 中得到解决,则我们可以得到下面的关键性引理:
引理2.4 设G是集合Ω上的本原置换群,令
为G的唯一极小正规子群,T为非交换单群,给定
。则G为以下情形之一:
1) 仿射型(HA):如果
。
2) 几乎单型(AS):如果
,
。
3) 单对角型(SD):如果N包含一个正规子群
作用在Ω上是正则的并且
。
4) 扭圈积型(TW):如果N在Ω上的作用是正则的。
5) 乘积作用型(PA):如果
,N不包含正规子群作用在Ω上正则。
引理2.5 [3] 设图
是一个连通的非平凡G-边本原图。则
是一个G-弧传递图,并且为下列情形之一:
1) Γ为G-顶点本原。
2) Γ为G-顶点二部本原。
3) Γ为G-边本原图
的spread且
为G-非局部本原图。
本文的主要研究内容即是刻画上述引理情形(1)中的边本原图。下面给出本文研究的关键性引理。
引理2.6 在定理1.1中的G为几乎单型。
证明 令
为G的基柱。由引理2.4可知则G可能为五种情形,下面逐一分析:
1) 若G为HA型,则
在
上正则,于是有
,故
,舍去。
2) 若G为SD型,则有
,其中T为非交换单群,
,
。由G在
上本原,则N在
上传递,因此有
。而由引理2.1可知T为可解群,矛盾。
3) 若G为TW型,则N在
上正则,则有
。而由引理2.1可知T为可解群,矛盾。
4) 若G为PA型,则
,其中
,由G在
上本原,则N在
上传递,因此有
,而由引理2.1可知T为可解群,矛盾。
证毕,故G只可能为几乎单型。
下面引理给出非平凡G-边本原图存在的一个必要条件。
引理2.7 设图
为一个非平凡G-边本原图,令
。则
且
整除
。
证明 由引理2.5可知
是连通的弧传递图,则有
并且
的度数
。并且有
,
整除
。
Li等人在 [15] 中分类了包含子群的指数为两个素数幂的乘积的本原置换群。从而我们可读出包含子群的指数为三的次幂倍奇素数幂的本原置换群。
本文我们仅考虑 [15] 中子群的指数是一个常数的情形,可得到下述的引理:
引理2.8 设T是几乎单型的本原置换群,H是T的子群且满足
,其中p为奇素数且
,a和b为正整数。则二元组
如表2所列。

Table 2. Non-abelian simple groups with a subgroup of index 3 a p b
表2. 具有子群的指数为
的非交换单群
3. 定理1.1的证明
在本节,我们考虑G在
上本原。通过引理2.6可知G是AS型的。令
,由T在
上传递,则
,
。由引理2.8可知
即为表2所列。由G在
的作用是忠实的,则G和T都可以看成
上的本原置换群。令
,由引理2.3可知G-边本原图的存在性需考虑边稳定子群
在G中是否极大。注:下文的证明将多次使用数学工具:Magma [16],Atlas [10]。
定理1.1的证明:
Row 1:设
,此时
,
。由Magma计算可知T在
上的秩为2,非平凡次轨道的长度为14,则
,
。而由Atlas知,G的极大子群的阶至少为
,故
在G中非极大,无边本原图例。
Row 2:设
,此时
,
。分为两种情形讨论:1) 当
时,由Magma计算可知,此时
没有指数为15的子群,故舍去。2) 当
时,由Magma计算可知,G在
上的秩为2,非平凡次轨道的长度为14,故
,
。由Atlas可知
的极大子群的阶至少为360,故舍去。
设
,分为两种情形讨论:1) 当
时,由Magma计算可知,G在
上的秩为3,非平凡次轨道的长度为16或18。故
或32,
或64,由Atlas可知
的极大子群阶数最小为360,舍去。2) 当
时,同理可知G在
上的秩为2,非平凡次轨道的长度为14,故
或64,
或128。由Magma计算可知
的极大子群的阶至少为336,故舍去。
Row 3:设
,此时
,
。1) 当
时,由Magma计算可知,此时
没有指数为2025的子群,舍去。2) 当
时,由Magma计算可知,G在
上的秩为4,非平凡次轨道的长度为330,462,1232,故
,
。而由Atlas可知McL的极大子群的阶至少为3000,舍去。
Row 4:设
,此时
,
。由文献 [3] 可知当
时,存在2-弧传递的边本原图,记为
。
Row 5:设
,此时
,
。1)
或
时,由Magma计算可知,G不存在指数为117的子群,故舍去。2) 当
时,由Magma计算可知G在
上的秩为3,非平凡次轨道的长度为36或80,故此时可计算得
或648,
或1296。由Atlas可知
恰有阶为2880的极大子群。故此时存在边本原图,记为
,并且由 [17] 可知,该图是1-弧传递的。
Row 6:设
,此时
。由Magma计算可知
在
上的秩为4,非平凡次轨道的长度为14,56,64。故此时可计算得
,
。由Atlas知,
没有阶为
的极大子群,故舍去。
设
,同理
。由Magma计算可知,
在
上的秩为3,非平凡次轨道的长度为30或32。故此时可计算得
或720,
或1440,由Atlas知,
没有阶为
的极大子群,故舍去。
Row 7:设
,此时
,
。由引理2.7可知,此时需满足
。而由Atlas可知,此时
恰好为G中阶最小的极大子群,故舍去。
Row 8:设
,此时
,
。1) 当
时,此时由Magma计算可知,G没有指数为567的子群,舍去。2) 当
,
时,可以通过Magma计算可知,G在
上的秩为5,此时非平凡次轨道的长度为30,96,120,320。故此时可计算得
,
。而由Magma计算G的极大子群L的阶
,故舍去。
Row 9:设
,此时
,
。分两种情形讨论:1) 当
时,由Magma计算可知,此时G在
上的秩为3,此时非平凡次轨道的长度为40或256。故此时可计算得
或180,
或360。由Atlas可知,
没有阶为
的极大子群,舍去。2) 当
时,同理可求得
或720。由Magma计算可知,
也没有阶为
的极大子群,舍去。
Row 10:设
,此时
,
。分两种情形讨论:1) 当
时,由Magma计算可知,此时G在
上的秩为4,此时非平凡次轨道的长度为42,336,512。故此时可计算得
,
。由Atlas可知,此时
有阶为40,320的极大子群。故此时存在边本原图,记为
,并且由 [17] 可知,该图是1-弧传递的。2) 当
,
时。由Magma计算易验证,仅存在与1) 同构的边本原图例子。
Row 11:设
,此时
,
。类似地,分两种情形讨论:1)当
时,由Magma计算可知,此时G在
上的秩为4,此时非平凡次轨道的长度为288,630,2240。故此时可计算得
,
。而由Atlas可知,
的极大子群的阶至少为13824,舍去。2) 当
时,由Magma计算可知,此时
没有指数为3159的子群,舍去。
设
,类似地,首先考虑1) 当
时,由Magma计算可知,此时G在
上的秩为3,非平凡次轨道的长度为126或224。故此时可计算得
或58,320,
或116,640。由Atlas可知,
恰有阶为207360的极大子群。故此时存在边本原图,记为
,并且由 [17] 可知,该图是1-弧传递的。2) 当
时,由Magma计算易验证,此时仅存在与1) 同构的边本原图例。
设
,此时
,
,若
为G的极大子群,通过Magma计算并且由Atlas可知,此时
只能为
或
,而
。计算可知
不整除
,这与引理2.7矛盾,舍去。
Row 12:设
,此时
,
。分两种情形讨论:1)当
,
时,由Magma计算可知G在
上的秩为3,非平凡次轨道的长度为64或70。故此时可计算得
或18,432,
或36,864。而由Atlas可知,G没有阶为
的极大子群,舍去。2) 当
,
时,G没有指数为135的子群,舍去。
Row 13:设
,此时
,
。首先考虑:1) 当有
,此时由Magma计算可知,G在
上的秩为6,非平凡次轨道的长度为960、960、960、3150、22,400。故此时可计算得
,55,296或7776,
,110,592或15,552。由Atlas可知,
没有阶为
的极大子群,舍去。2)
,
。类似情形1),由Magma易验证也无
在G中极大,舍去。
Row 14:设
,此时
,
。分两种情形讨论:1) 当
时,由Magma计算可知,G在
上的秩为3,非平凡次轨道的长度为378或728。故此时计算得
或12,597,120,
或25,194,240。由Atlas知
恰好有阶为48522240的极大子群。故存在边本原图,记为
,并且由 [17] 可知,该图是1-弧传递的。2) 当
,
时,由Magma验证可知仅存在与1) 同构的边本原图例。
Row 15:设
,此时
,
。由Magma计算可知,G在
上的秩为3,非平凡次轨道的长度为126或224。故此时计算得
或
,
或
。由Atlas可知,G的极大子群的阶至少为
,舍去。
设
,若
为G的极大子群,通过Magma计算并且由Atlas可知,此时
只能为
或
,而
。计算可知
不整除
,这与引理2.7矛盾,舍去。
基金项目
云南省科技厅应用基础研究项目(2019FD116)资助。