乙醇偶合制备C₄烯烃的合理优化

Optimum Preparation of C₄ Olefin by Ethanol Coupling

摘要: 作为重要的基础化工原料，C₄烯烃被广泛应用于化工产品及医药中间体的生产。乙醇是生产制备C₄烯烃的重要原料，在制备过程中，C₄烯烃的收率一定程度上取决于反应温度和反应的催化剂组合，所以如何合理地设计催化剂组合及温度至为关键。本文为探究不同反应条件对乙醇转化率及C₄烯烃选择性的影响，建立基于OLS + 稳健的标准误的多元线性回归模型，得到对乙醇转化率及C₄烯烃选择性线性相关显著的影响因素，并计算标准化回归系数，对影响因素的重要程度进行排序。为确定最佳反应条件，建立逐步筛选模型，并用MATLAB分别对C₄烯烃收率与单变量进行曲线拟合。采用粒子群优化算法，依次确定C₄烯烃收率最高时，各变量的最佳取值。

Abstract: As an important basic chemical raw material, C₄ olefins are widely used in the production of chemical products and pharmaceutical intermediates. Ethanol is an important raw material for the production and preparation of C₄ olefin. In the preparation process, the yield of C₄ olefin depends on the reaction temperature and catalyst combination, so how to design the catalyst combination and temperature reasonably is the key. In order to explore the effects of different reaction conditions on ethanol conversion and C₄ olefin selectivity, a multiple linear regression model based on OLS + robust standard error was established to obtain the influential factors with significant linear correlation on ethanol conversion and C₄ olefin selectivity. The standardized regression coefficient is calculated to rank the importance of the influencing factors. In order to determine the optimal reaction conditions, a stepwise screening model was established, and the curve fitting between the yield of C₄ olefin and single variable was carried out by MATLAB. Finally, particle swarm optimization algorithm was used to determine the optimal value of each variable when the yield of C₄ olefin was the highest.

1. 引言

C₄烯烃是工业生产及医药生产过程中的重要化工原料，如何在满足节能、清洁要求的同时高效制备C₄烯烃显得尤为重要。传统的工业生产方式采用化石能源为原料，但随着经济的快速发展和人们环保意识的提高，更倾向于采用绿色清洁能源，乙醇来源广泛，绿色清洁，以其为平台化合物生产高附加值产物具有很大的应用前景及经济效益。

在乙醇偶合制备C₄烯烃的过程中，催化剂组合中Co负载量、乙醇浓度、Co/SiO₂和HAP装料比、装料方式和反应温度都会对乙醇转化率和C₄烯烃的选择性产生影响 [1]，从而影响C₄烯烃的收率。传统利用改变实验条件多次重复实验，来对比实验结果，从而逐步缩小条件范围，来确定最佳反应条件的方法会消耗大量时间精力，同时在一定程度上也会造成资源浪费，所以利用现有有限的实验数据建立数学模型探究各因素的影响程度，并且确定可以使C₄烯烃收率达到最大的反应条件，在实际实验中可以进行针对性的调整，在一定程度上也可以减少时间、精力、资源的消耗，从而使生产效率最大化。

2. 探究催化剂和温度对反应的影响

为探究不同催化剂组合及温度对乙醇转化率、C₄烯烃选择性大小的影响，且催化剂组合中存在多个影响因素，因此采用回归方法探究多因素对反应的影响，首先对催化剂组合中的因素进行拆分，将温度、乙醇浓度、Co/SiO₂和HAP装料比、Co负载量、催化剂总重这五个因素作为自变量( $x_1~x_5$ )，乙醇转化率和C₄烯烃选择性作为因变量。用部分数据建立模型，并进行显著性差异检验。具体步骤如下：

Step 1：随机选取n组数据为实验组数据，建立基于普通最小二乘估计法的回归模型，其余数据为检验组。

Step 2：检验是否存在异方差并对模型进行改进。

Step 3：确定最终模型并对回归结果进行显著性检验，并验证模型的可行性。

Step 4：计算标准化回归系数进一步确定自变量对因变量影响的重要程度。

2.1. 模型建立

涉及5个自变量的多元线性回归模型 [2] 可表示为：

$\{\begin{array}{l}y={\omega }_0+{\omega }_1{x}_1+{\omega }_2{x}_2+{\omega }_3{x}_3+{\omega }_4{x}_4+{\omega }_5{x}_5+\epsilon \\ \epsilon ~N\left(0,{\sigma }^2\right)\end{array}$

为了方便推导，通过n组实验数据引入矩阵符号分析：

$Y=\left[\begin{array}{c}{y}_1\\ y_n\\ ⋮\\ y_n\end{array}\right]$， $X=\left[\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{15}\\ x_{21}& x_{22}& \cdots & x_{25}\\ ⋮& ⋮& & ⋮\\ x_{n1}& x_{n2}& \cdots & x_{n5}\end{array}\right]$， $\omega =\left[\begin{array}{c}{\omega }_0\\ {\omega }_1\\ ⋮\\ {\omega }_5\end{array}\right]$， $\epsilon =\left[\begin{array}{c}{\epsilon }_1\\ {\epsilon }_n\\ ⋮\\ {\epsilon }_n\end{array}\right]$

其中X为模型设计矩阵，X为常数矩阵，Y与 $\epsilon$ 是随机向量，

$Y~N_n\left(X\beta ,{\sigma }^{2}I\right)$， $\epsilon ~N_n\left(0,{\sigma }^{2}I\right)$ (I为n阶单位矩阵)

$\omega$ 为需求回归系数， $\epsilon$ 为不可观测的随机误差。

2.2. 模型求解

以温度、乙醇浓度、Co/SiO₂和HAP装料比、Co负载量、催化剂总重这五个因素作为自变量，分别记作 $x_1~x_5$，以乙醇转化率、C₄烯烃选择性作为因变量，利用实验组数据进行基于普通最小二乘估计法的多元线性回归分析，模型通过了显著性检验，画出残差与拟合值的散点图，如图1所示。

Figure 1. Residual and fitting values scatter plot

图1. 残差与拟合值散点图

从图1中可以看出，扰动项存在异方差。对异方差进行怀特检验，证明了异方差确实存在。因此，在此基础上对模型进行改进，使用OLS + 稳健的标准误再次进行回归，分别得到温度及催化剂组合对乙醇转化率、C₄烯烃选择性的回归方程：

1) 乙醇转化率：

$y=0.555x_1-7.183x_2+0.0514x_5-87.892$

2) C₄烯烃选择性：

$y=0.192x_1+2.914x_2+3.248x_3-293.508x_4+0.0453x_5-55.499$

2.3. 显著性检验

在进行结果分析之前，对两组回归结果分别进行检验 [3]：

a) 模型F检验

Table 1. Test results

表1. 检验结果

由表1可知，P = 0.0000 < 0.0001，上述模型通过了联合显著性检验，且置信度达到99%以上。

b) 回归系数显著性检验

Table 2. Significance test of regression coefficient of ethanol conversion

表2. 乙醇转化率回归系数显著性检验

注：^***p < 0.01，^**p < 0.05，^*p < 0.1。

如表2，其中装料比与Co负载量的偏相关系数没有通过显著性检验，说明装料比和Co负载量对乙醇转化率线性相关不显著，其余自变量均线性相关显著。

Table 3. Significance test of C4 olefins selective regression coefficient

表3. C₄烯烃选择性回归系数显著性检验

注：^***p < 0.01，^**p < 0.05，^*p < 0.1。

如表3，其中乙醇浓度和装料比与烯烃选择性在90%的置信水平上线性相关显著，其余在99%的置信水平上线性相关显著。

c) 多重共线性检验

考虑自变量之间是否有相关性，此时将对回归系数估计不准确，引入方差膨胀因子VIF，假设有k个自变量，那么对第m个自变量的方差膨胀因子定义为：

$VI{F}_m=\frac{1}{1-R_{1-k/m}^2}$

其中 $R_{1-k/m}^2$ 是将第m个自变量作为因变量对剩下的 $k-\text{1}$ 个自变量进行回归得到的拟合优度。 $VI{F}_m$ 越大，说明第m个变量和其他变量的相关性越大，利用该规则进行多重共线性检验：

Table 4. Multicollinearity test

表4. 多重共线性检验

由表4可以看出，各自变量的VIF < 10，通过多重共线性检验。

d) 回归结果的检验

利用检验组数据对模型的可行性进行验证，样本实验数据与拟合值如下图2、图3：

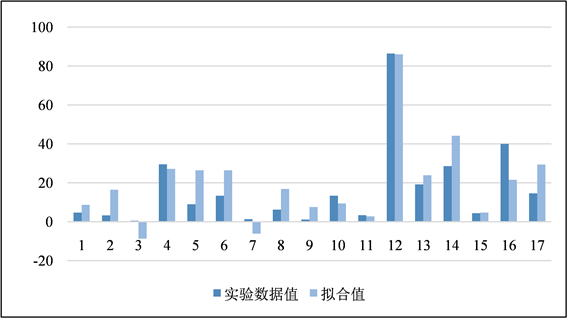
Figure 2. Ethanol conversion rate data contrast

图2. 乙醇转化率数据对比

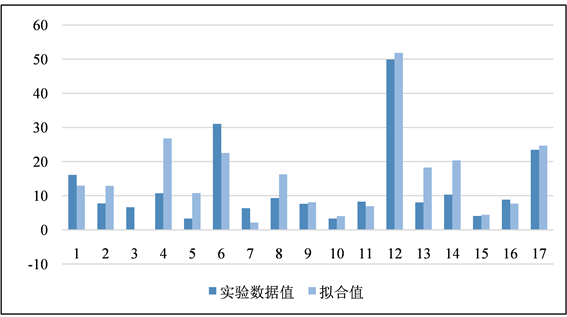
Figure 3. C₄ olefins selectivity data contrast

图3. C₄烯烃选择性数据对比

利用SPSS进行Wilcoxon符号秩检验，由于实验数据较少且无法对分布形态做简单假定，因此使用非参数检验来确定多元线性回归模型的计算值与实际的实验数据是否有显著性差异。其中，H₀：两组数据值无显著性差异，H₁：两组数据值有显著性差异。

Table 5. Wilcoxon sign rank test results

表5. Wilcoxon符号秩检验结果

由表5可知，p > 0.05，故接受原假设，认为通过模型计算的数据和原始实验数据没有显著性差异，得到的线性回归方程可信。

2.4. 结果分析

由上述回归结果可以剔除对C₄烯烃收率影响不显著的自变量，为了更精准的研究显著自变量对因变量影响程度，计算出标准化回归系数，标准化系数的绝对值越大，说明对因变量的影响程度越大，根据计算结果，对乙醇转化率影响由高到低依次为温度 > 催化剂总重 > 乙醇浓度，对C₄烯烃选择性影响由高到低依次为温度 > 催化剂总重 > Co负载量 > 乙醇浓度。

3. 确定最佳反应条件

在上述模型结果的基础上，采用基于控制变量思想的逐步筛选法，将催化剂组合中的5个自变量对C₄烯烃收率的影响分别分析。其次使用MATLAB工具箱对C₄烯烃收率与单变量进行曲线拟合，并进行检验。最后，选用粒子群优化算法 [4] [5] 对逐步筛选出的数据求解最佳取值。

3.1. 模型建立

建立基于控制变量思想的逐步筛选法使C₄烯烃收率最大化的模型。

控制变量法的思想是每一次只改变其中的某一个因素，而控制其余几个因素不变，从而研究被改变的这个因素对事物的影响，分别研究各因素，最后再综合解决，它是科学探究中的重要思想方法。

逐次筛选法的思想是按照自变量的重要程度，依次控制单变量对数据进行分析，从而逐步求解C₄烯烃的最大收率。

模型过程如下图4：

Figure 4. Model process diagram

图4. 模型过程图

3.2. 模型求解及分析

依据上述思想确定最佳反应条件，阅读相关文献 [1] 了解到Co/SiO₂和HAP装料比为1:1时，C₄烯烃的收率达到最高。因此，将其作为假设，并从实验数据中，挑选出仅装料比不同的数据进行绘图，并对假设进行检验。其C₄烯烃收率的柱状图如图5所示。

从图5中可以看出，在其他4个因素保持不变的情况下，无论处于哪种温度条件下，Co/SiO₂和HAP装料比为1:1时，C₄烯烃收率均达到最大值，所以将Co/SiO₂和HAP装料比设定为1:1作为初始情况。

装料比为1:1即为定值，控制催化剂总量为400 mg、乙醇浓度为1.68 ml/min、Co负载量为1 wt%不变，将温度作为变量，筛选出新的数据，记为数据a，为拟合C₄烯烃收率与温度的函数提供数据。

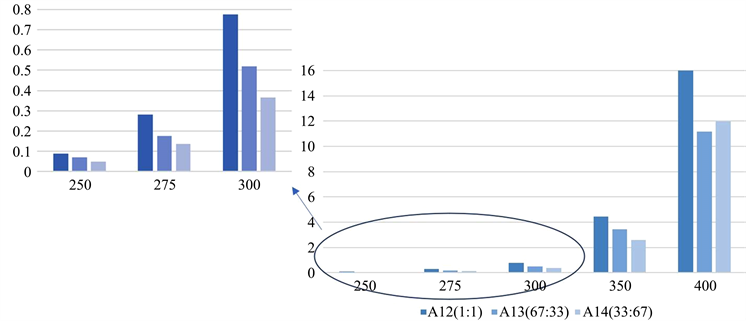
Figure 5. C₄ olefin yield of three charge ratios at different temperatures

图5. 不同温度下三种装料比的C₄烯烃收率

进而，在数据a的基础上，将计算得到的最优装料比1:1和温度400℃作为定值，并保持乙醇浓度为1.68 ml/min、Co负载量为1 wt%不变，催化剂总重为变量，进一步筛选出符合的数据，记为数据b，为拟合C₄烯烃收率与催化剂总量的函数提供数据。

最后，由于满足条件的实验数据较少，仍将已经计算得到的最优装料比1:1和温度400℃作为定值，并保持Co负载量为1 wt%、催化剂总重为100 mg不变，乙醇浓度为变量，筛选出符合的数据，记为数据c，为拟合C₄烯烃收率与乙醇浓度的函数提供数据。

3.3. C₄烯烃收率与单变量的曲线拟合

采用MATLAB Curve Fitting工具箱对已处理的数据进行曲线拟合，并计算已调整后的R方进行曲线拟合效果的检验，为求解C₄烯烃收率的最优值做准备。

· C₄烯烃的收率与温度的拟合函数：

$\begin{array}{l}Y=17.04\ast \exp \left(-{\left(\left(x-400\right)/8.389\right)}^2\right)+4.724\ast \exp \left(-{\left(\left(x-350\right)/7.481\right)}^2\right)\\ +0.8007\ast \exp \left(-{\left(\left(x-300\right)/5.761\right)}^2\right),R^2=0.9958\end{array}$

· C₄烯烃的收率与催化剂总重的拟合函数：

$Y=19.41\ast \exp \left(-{\left(\left(x-176.1\right)/72.22\right)}^2\right)+11.42\ast \exp \left(-{\left(\left(x-86.41\right)/49.96\right)}^2\right),R^2=0.9771$

· C₄烯烃收率与乙醇浓度的拟合函数：

$Y=27.94\ast \exp \left(-{\left(\left(x-0.3372\right)/0.7401\right)}^2\right)+16.02\ast \exp \left(-{\left(\left(x-1.877\right)/0.6187\right)}^2\right),R^2=0.9207$

· C₄烯烃收率与Co负载量关系的函数：

$\begin{array}{l}Y=9.493\ast \exp \left(-{\left(\left(x-0.02\right)/0.001747\right)}^2\right)+5.33\ast \exp \left(-{\left(\left(x-0.01\right)/0.002555\right)}^2\right)\\ +5.151\ast \exp \left(-{\left(\left(x-0.005\right)/0.004494\right)}^2\right),R^2=0.9283\end{array}$

3.4. 求解最佳温度与催化剂组合

利用粒子群优化算法，对C₄烯烃收率与单变量拟合出的函数进行最优值求解，探讨出在相同实验条件下能够使得C₄烯烃收率尽可能高的催化剂组合和温度。

算法的步骤大致分为以下五步：

① 设置粒子速度的区间，对粒子群进行初始化。

② 计算粒子的适应值。

③ 全局搜索粒子个体的极值，并对当前最优解和历史最优解进行比较，选择出当前历史的最优解。粒子更新迭代公式为如下：

$v_i=v_i+c_i\times rand\left(\right)\times \left(pbes{t}_i-x_i\right)+c_2\times rand\left(\right)\times \left(gbes{t}_i-x_i\right)$

$x_i=x_i+v_i$

④ 寻找全局的最优解。据图公式如下：

$v_i=\omega \times v_i+c_i\times rand\left(\right)\times \left(pbes{t}_i-x_i\right)+c_2\times rand\left(\right)\times \left(gbes{t}_i-x_i\right)$

${\omega }^{\left(t\right)}=\left({\omega }_{ini}-{\omega }_{end}\right)\left(G_k-g\right)/G_k+{\omega }_{end}$

⑤ 粒子之间进行比较并修改粒子的速度和位置，并设置使得粒子停止迭代的条件。

将MATLAB拟合并通过检验的函数代入粒子群优化算法中，可以计算得到最佳催化剂组合和温度，结果如图6所示：

Figure 6. Solving results

图6. 求解结果

结果显示，当温度为399.9999℃，催化剂总重169.6884 mg，乙醇浓度为0.33982 ml/min，Co负载量为0.020001，即2.0001 wt%时时，C₄烯烃收率达到最高。综合以上，最佳温度及催化剂组合的选择如表6所示。

Table 6. Optimal reaction conditions

表6. 最佳反应条件

4. 总结

在本文中，为探究各因素对反应的影响，将数据分为两组，利用检验组对所求结果进行WilCoxon符号秩检验，相比于用所有数据用于回归模型，增设模型检验，因而模型更具可信度。在求解最佳反应条件时，提出基于控制变量思想的逐步筛选法，改善了数据处理的方式，对解决多变量问题进行简化。

本文所建立的基于OLS + 稳健标准误的多元线性回归模型以及对于该模型效果的检验方法，可适用于探究其他化学反应中反应条件对产物收率的影响，并确定影响产物收率的关键因素。基于控制变量思想的逐步筛选模型可适用于实验数据较少时，求解产物收率最优化问题。上述模型可推广至其他工业生产中，具有一定的参考价值与经济意义。