挖掘装置四杆机构的优化设计

Optimized Design of the Four-Bar Mechanism of the Excavation Device

摘要: 为了便于小地块栽花、植树方便，设计出一款仿穿山甲式半自动挖坑机，其挖掘动作由四杆机构执行，本文对此四杆机构进行优化设计。首先借助图谱法找到适合要求的运动轨迹，进而确定构件最初尺寸。应用ADAMS对挖掘装置进行建模，并对模型进行参数化设置和添加约束条件，对工作阶段四杆机构的连杆和挖具的速度及其加速度进行分析，得到其在运动过程中的各项力学指标。其次，使用MATLAB软件进行进一步的分析，以减重为目标对机构进行结构优化以获得最佳的构件尺寸。最后运用CREO软件对主要构件进行静力学分析以验证其强度。

Abstract: In order to facilitate the planting of flowers and trees in small plots, a semi-automatic digging machine imitating pangolins is designed, and its excavation action is performed by a four-bar mechanism. This paper optimizes the design of this four-bar mechanism. Firstly, the trajectory of the suitable requirements is found by means of Atlas Method, and the initial dimensions of the components are determined. Adams is used to model the excavation device, parameterize the model and add constraints, analyze the speed and acceleration of the connecting rod and excavator of the four-bar mechanism in the working stage, and obtain various mechanical indexes in the movement process. Secondly, further analysis is carried out using MATLAB, and the structure of the mechanism is optimized with the goal of weight reduction to obtain the optimal component size. Finally, the main components are statically analyzed using CREO software to verify their strength.

1. 引言

随着可持续发展战略规划的提出，环境保护理念的提升，大规模植树造林和城市绿化受到了广泛关注，尤其是小面积不规则地块的栽花种草的挖掘工作强度变得越来越大，为了省力、提高挖坑效率，作者设计了一款可以遥控的半自动挖坑装置。该装置运用仿生学的原理，模仿穿山甲挖土的动作，在挖掘过程中要求运动要求平稳，效率高，力学性能好。平面四杆机构在机械制造业被广泛使用，可以直接对运动轨迹与运动规律给出指导，完善预订完成的工作，所以大量应用在制造业、农业、纺织业、重型工业等众多领域。因此选用了简单经济的平面四杆机构。

平面连杆机构传统的设计方法有图解法、解析法、图谱法，因为图解法需要作图找到杆的极限位置关系，进而确定杆的运动轨迹，验算压力角和传动角是否满足要求，是否存在死点；解析法要采用机构的尺寸参数来表达各个构件之间的相对位置关系，建立相应的方程组来对未知数进行求解，但穿山甲爪子的动作轨迹是条曲线，目前没有精确的表达式，不便于用图解法和解析法，可以利用图谱法近似求解，但是此方法精度不高，可以通过优化设计使设计的连杆机构尽可能符合要求还能对其性能进行分析。在众多优化设计方法中，多体动力学分析软件ADAMS避免了复杂的数学公式推导和繁琐的编程，可以提高优化设计的速度，从而缩短设计周期。

本文以穿山甲式半自动挖坑机上的四杆机构进行分析，在ADAMS软件中建立其动力学模型，对其进行运动仿真，获得仿真曲线，对获得的数据进行力学分析，运用MATLAB软件对获得的数据进行统计分析，得到最佳的参数。以这组参数为基础运用CREO软件建立三维建模进行有限元分析，以省材，轻便为目标，进行了机构的优化。

2. 挖掘装置四杆机构的简化模型和性能要求

2.1. 挖掘装置四杆机构的简化模型

通过CAD软件绘制出挖掘装置四杆机构的机构简图如图2，便于之后的分析与研究。以曲柄BD为原动件，通过连杆CD带动摇杆AC摆动，CD杆末端装有挖具，连杆的运动实现了对土地的挖掘。

2.2. 挖掘装置四杆机构性能要求

为了既满足性能的需要同时减轻装置的重量，因此需要对机构进行力学分析，在满足材料各项要求的条件下，对机构的形状进行优化。

3. 挖掘装置四杆机构尺寸确立

通过分析穿山甲在挖掘时爪子的运动方式，运用图谱法 [1] 找到一个合适的运动轨迹再使用CREO软件进行大量的轨迹模拟实验，最终得到了几组与穿山甲爪子运动轨迹相符合的杆长关系如图1，经过仔细的计算确立了合适的各构件长度之间的比例关系为AB:AC:BD:CE = 3:2:1:4，符合杆长条件，为满足实际的工作需要最终各构件长度确定为75 cm，50 cm，25 cm，100 cm。

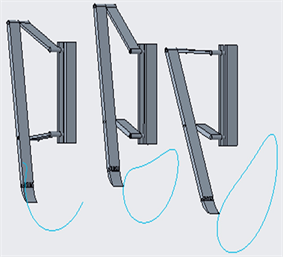
Figure 1. Simulation of paw trajectory curve

图1. 爪子轨迹曲线模拟

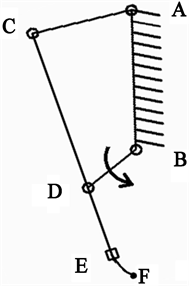
Figure 2. Schematic diagram of the four-bar mechanism of the excavator

图2. 挖掘装置四杆机构简图

4. 挖掘装置四杆机构ADAMS建模与仿真

4.1. 四杆机构几何模型的建立

根据图2中各关键点的坐标，原点取在B点，在ADAMS中建立几何模型如图3所示，添加实验用的材料参数。(本实验使用材料为铝合金)

4.2. 添加约束

对于建好的几何模型，首先给互相连接的构件之间添加运动副约束，AB杆为固定约束，其次在主动曲柄上添加驱动，主动曲柄转速设为180˚/s系统默认为逆时针方向，最后在挖具上加上生产阻力，添加方式为单向阻力。

Figure 3. Model of the four-bar mechanism of the excavator

图3. 挖掘装置四杆机构模型

4.3. 四杆机构运动仿真

为了得到四杆机构在运动过程中的速度参数和加速度参数，调用ADAMS软件仿真程序添加仿真时间为2 s，即四杆机构运动一个周期，步长设为0.05步，进行多次运行仿真后通过对测量得到的挖具质心的速度和加速度数据参数进行误差检查，得到一组较为准确的周期变化曲线，如图4、图5所示。从中可以得到最大运动速度为1.12 m/s，最大加速度2.19 m/s²。

Figure 4. Velocity curve of point F

图4. F点速度曲线

5. 挖掘装置四杆机构的优化

5.1. 确定设计变量

挖掘装置四杆机构中的连杆是传递动力和承受压力的主要零件，除了选择材料、热处理工艺等条件外，还应该确定连杆上D点轴的半径R (见图1)、连杆CE的厚度S、连杆宽度D₁、爪子的厚度C。因此得到设计变量为： $X={\left(C,S,R,D_1\right)}^{\text{T}}$。

Figure 5. Acceleration curve at point F

图5. F点加速度曲线

5.2. 建立目标函数

机构要求在重量尽量轻的情况下还应该满足工作时各部件的强度刚度要达到求，并且可以完成特定的工作轨迹，实现目标工件的顺利进行，因此以机构重量最小进行优化 [2]。根据几何关系可以计算爪子和杆件的重量：

爪子重量：

$W_{爪}=lgdC\rho W_{爪}$

其中 、 $d$ 为爪子工作面边长。由CREO软件测得l = 10.5755 cm，d = 10 cm，ρ = 97.85 g/cm³，g = 980 cm/s²。

连杆重量：

$W_{杆}=LDS\rho g$

其中：L为连杆长度，取L = 100 cm。

目标函数为： $W_{总}=W_{爪}+W_{杆}$。

5.3. 约束条件

考虑到许用应力以及等界限问题，均存在有从完全许用到完全不许用的过渡区间，这样得约束条件如下：

1) 强度条件

$G_1\left(X\right)={\delta }_{bs}=\frac{R_X+F}{A}\le \left[\tau \right]$ (1)

式中：R_x为土壤阻力，由高略契金有理公式 [3]： $G_2\left(X\right)=Fg+kdb+\epsilon db{V}^2$，其中d = 10 cm为工作时的作用宽度，b = 2 cm为作用深度。F = ma = 4.14 N (m为爪子质量，a为加速度，运动分析中已经求出)， $A=dC$，[τ] = 177.4 Mp为材料的许用剪切应力。

$G_3\left(X\right)=\delta =\frac{M}{W_Z}\le \left[\delta \right]$ (2)

式中：M为作用在D点的弯矩 $M=\left(Rx+F\right)L$，W_z为连杆的抗弯截面系数 $W_Z=D_1{S}^2/6$，[σ]为材料的许用压应力，硬铝合金的许用压应力为221.8 Mpa。

$G_4\left(X\right)=\tau =\frac{F_q}{\text{π}}\times R^2\le \left[\tau \right]$ (3)

式中：Fq为D点轴与孔之间的作用力。

2) 设计变量取值界限

$0.5=C_{\min }\le C\le C_{\max }=1(\; cm\; )$

$1.5=S_{\min }\le S\le S_{\max }=3(\; cm\; )$

$0.5=R_{\min }\le R\le R_{\max }=1.0(\; cm\; )$

$5=D_{1\min }\le D_1\le D_{1\max }=10(\; cm\; )$

5.4. 优化设计

根据目标函数，强度条件G₁(X)、G₃(X)、G₄(X)以及设计变量 $X={\left(C,S,R,D_1\right)}^{\text{T}}$。在SimMechanics环境中，利用各构件之间的关系进行物理建模，实现构件、铰链、坐标系统等组成部分的建模和仿真，能对机构铰链约束处的受力进行求解，同时对机构实现实时动画显示。根据挖掘装置四杆机构的工作的关系，建立SimMechanics仿真模型，根据杆件的质量、转动惯量、尺寸等设置模块参数。对模型添加完约束条件和目标函数，运用MATLAB进行编程完成优化 [4]。优化前、后各参数对比表1所示。

Table 1. Comparison of parameters before and after optimization cm

表1. 优化前后参数对比cm

连杆的重量从原来8.10 kg的优化到现在3.25 kg，连杆的重量优化60%。运用优化设计得到的数据可以得出整个挖掘四杆机构重量优化53.2%。通过运用MATLAB进行优化设计，节约了大量验算的时间而且精度也得到了很好的保证。

5.5. 有限元分析

有限元分析是用较简单的问题代替复杂问题后再求解。它将求解域看成是由许多称为有限元的小的互连子域组成，对每一单元假定一个合适的近似解，然后推导求解这个域总的满足条件，从而得到问题的解。为检验连杆受力情况，分别取连杆的C、D、E、F点为研究对象，根据优化设计的得到的数据利用CREO软件绘制出连杆和爪子的三维建模，运用该软件中Simulate功能，对各点施加相应的载荷，并在CREO软件进行有限元分析 [5] [6]。

第一步，参数设定：本文实例使用的材料为铝合金，因此参数设计为弹性模量为72,000 Mpa，泊松比为0.3。

第二步，施加载荷：对爪子施加F = 124913.7 N的均匀作用力，做为在运动过程中的工作阻力。

第三步，施加约束：四杆机构的杆与杆之间通过销钉链接，因此在C、D两点为销轴约束，为保证爪子在运动中的稳定性需要其与连杆焊接在一起，因此，进行有限元分析时E点与爪子为固定约束。

第四步，结果计算与分析：载荷及约束施加情况如图6，分析结果如图7、图8。

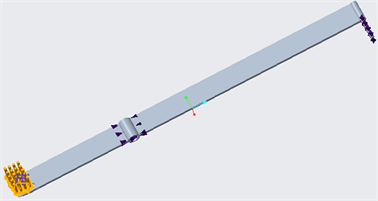
Figure 6. Distribution diagram of load and constraint

图6. 载荷及约束施加分布图

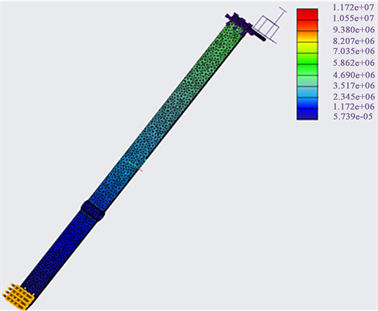
Figure 7. Linkage stress distribution diagram

图7. 连杆应力分布图

Figure 8. Maximum stress point

图8. 最大应力点

通过CREO有限元分析得到四杆机构中连杆最大应力值为11.72 Mpa，满足材料强度要求和挖掘装置工作要求，并且由程序得到的连杆数据和仿真后的运动参数相差不大，即具有较高可信度。

6. 结语

1) 利用四杆机构作为挖掘装置，通过研究其爪子的运动轨迹，通过图谱法得到需要的爪子运动轨迹的构件长度。

2) 利用ADAMS软件建立参数化的挖掘四杆模型，并对其进行运动仿真得到机构F点的最大运动速度为1.12 m/s，最大加速度2.19 m/s²。

3) 通过MATLAB软件优化得到的连杆和爪子结构的最佳参数满足材料和工作要求。由程序得到的四杆机构运动参数与仿真后输出的参数相差不大，连杆的重量从原来8.10 kg的优化到现在3.25 kg，连杆的重量减重60%。

4) 运用软件CREO对连杆和爪子的静力学分析表明在该组参数下连杆和爪子满足工作强度要求。