1. 引言
软件可靠性工程是软件开发的一个重要部分,在该领域的研究也越来越多。软件可靠性模型在软件可靠性工程概念领域发挥着至关重要的作用;它可以在测试阶段的某个阶段为软件开发和质量保证团队提供相当有价值的信息。软件可靠性有助于降低公司的故障风险、提高信息安全和技术。实施软件可靠性模型可以提高生产力,减少维护费用和故障成本。确保软件无故障是软件应用程序开发行业的一个重要问题。软件质量涵盖了一些关键因素,如软件可靠性、可维护性、可用性、在恶劣环境下的性能、稳健性以及对用户的数据保护。其中,软件可靠性是最重要的尺度;如果开发者不注意,它可能会影响公司的发展。软件可靠性关注所有类型的错误和故障,这些错误和故障可能影响任何类型的软件应用程序提供预期的解决方案的过程。对软件开发者来说,确定软件的确切可靠性并不是一件容易的事。
对软件可靠性建立正确的模型并预测其可能的增长趋势,对于整个软件的可靠性至关重要 [1] [2] [3]。软件可靠性增长模型SRGM已有众多模型被提出。在当前研究中,非齐次泊松过程(non-homogeneous Poisson process)类软件可靠性增长模型应用最为广泛;其中G-O模型 [4] 最为经典,其假设软件系统被检查出的累计故障数是泊松分布,并指出软件错误的内在数量是随机变量,对软件可靠性模型的开发作出了重要贡献。论文 [5] [6] [7] 中先后对G-O模型的假设作了不同的修改、完善,并提出了各种不同的模型。这些模型的应用需要基本的假设,如故障之间的时间独立,检测到的故障立即被纠正,以及故障纠正过程不引入新的故障。然而,其中一些假设似乎是不现实的 [8]。此外,SRGM的适用性已成为一个关键问题,因为没有一个单一的模型可以在所有情况下普遍使用 [9]。关于SRGM的可预测性,作为使用SRGM的主要目标,这些模型已经被证明能够对过去的软件故障数据进行建模和拟合,然而,它们并没有给出准确的预测。
因此一些研究人员试图将时间序列模型,特别是ARIMA模型应用于可靠性预测。主要结果是,时间序列模型可以解决SRGM的问题,而且它们有能力给出更准确的预测结果。此外,Junhong等人 [10] 证明了软件可靠性预测中最常用的Goel-Okumoto NHPP模型可以转化为一阶自回归模型(AR(1))。这一结果说明,最重要的软件可靠性模型是ARIMA模型的一个特例,这为如何在软件可靠性预测中利用ARIMA模型的优势开辟了一个新的研究领域。胡和谢 [11] 讨论了不同类型的ARIMA模型,用于预测软件系统的故障。作者将ARIMA模型与Duane模型进行了比较。Duane模型是基于非齐次泊松过程实现的,ARIMA是一个线性模型,它是针对Duane模型提出的,作者对这些模型进行了分析以预测软件系统的数据故障。最后ARIMA模型被认为是更好的预测模型。Fan和Fan [12] 提出了用时间序列评估工业软件系统的软件可靠性分析和故障预测方案。研究发现,时间序列模型是一种可行的替代方法,就其对建筑设备可靠性的预测性能而言,对点故障和间隔故障的预测都能给出满意的结果。Amin等人 [13] 提出了软件可靠性增长预测中的时间序列模型,作者认为在预测系统中使用不现实的假设在可靠性预测中没有意义,故提出了一种成熟的预测方法,它可以帮助软件可靠性工程师以更简单的方式构建正确的预测模型,从而提供相对于其他现有方法更准确的可靠性预测结果。Cao [14] 提供了一个结合ARIMA模型与分形的线性和非线性建模的混合方案,并提出了一种研究软件失效机制的新思路。Choudhary [15] 提出了使用机器学习技术或时间序列建模的非参数化软件可靠性增长模型。Pati和Shukla [16] 提出将人工神经网络和求和自回归滑动平均模型的混合算法,这种整合有助于获取线性和非线性的故障模式。在这项工作中,线性和非线性部分被分别用来评估,以提高软件的可靠性。Chen等人 [17] 提出了一种基于深度学习的方法,利用时间序列数据进行设备可靠性分析。Wang等人 [18] 提出一种改进的时间序列方法应用于电力系统可靠性,并与传统的时间序列算法和蒙特卡洛方法进行比较。Kumaresan等 [19] 提出了成熟的统计时间序列(S)ARIMA方法来开发一个预测模型,作者首先根据数据结构,对模型的适配能力进行评估。如果数据集的行为是线性的,则会选择ARIMA模型。如果是非线性的,那么(S)ARIMA模型将被采用。在进行(S)ARIMA模型之前,它要找到系统中的季节性。Kamlesh等 [20] 在季节性ARIMA模型基础上提出了一个基于故障分类的故障预测模型。综上,目前时间序列可靠性模型仅将软件看作一个整体,即使用软件的总故障数据进行建模,对于包含多组件的复杂软件,并未考虑组件之间的相关性以及对组件分别进行建模。
基于以上所述,本文的突破在于利用VAR模型建立了一个多变量约束的软件可靠性模型,以克服目前软件可靠性分析中单变量模型的缺陷,以及在多变量模型的情况下没有考虑成分间相关性的影响。所提出的基于向量自回归的软件可靠性预测模型被应用于两个真实的软件故障数据集,并与用于软件可靠性分析的ARIMA和G-O模型进行比较,在数据集1中,本文提出模型对于G-O模型和ARIMA模型拟合相对精度分别提高了42.23%和30.88%;在数据集2中,拟合相对精度分别提高了6.038%和1.299%。对于预测效果而言,在两个数据集中,对于G-O模型的相对精度分别提高了37.893%和18.176%,对于ARIMA模型分别提高了1.076%和12.418%。因此认为本文所提出的多元时间序列分析方法可以更完整、更全面地描述软件的可靠性,更准确地预测软件故障的发生。
2. 基于VAR模型的软件可靠性分析方法
2.1. VAR模型预测结构
本文选用Christopher Sims在1980年 [21] 提出的向量自回归模型作为实证研究的方法,并利用R软件进行建模。
VAR模型的数学表达式为:
(1)
式(1)中:
是一个
维常数向量,并且对于
,
是
维矩阵,
,
是独立同分布
随机向量序列,其均值为0,协方差矩阵为正定矩阵。
可将VAR模型展开为如下形式:
(2)
VAR模型将所有变量纳入模型并对变量之间的关系进行更全面的分析。其一般流程为:1) 观察一段时间内的实验数据,检查并满足VAR模型的平稳性假设;2) 确定适当的VAR模型来描述这些数据;3) 使用估计方法拟合确定的模型;4) 检查估计模型的适当性;最后5) 使用构建的预测模型来预测未来值。
2.2. 基于VAR模型的软件可靠性建模
本节将构造基于VAR模型的软件可靠性模型,将软件组件的故障数据代入(1)式得如下式(3):
(3)
其中
代表第
个组件。
2.3. 参数估计
2.3.1. 模型定阶
VAR模型滞后期的选择对模型分析的准确性至关重要。较小的k值会导致误差项的严重自相关,而k值过大会导致自由度的减少,大大影响参数估计的有效性。在本文中,将综合考虑各准则来进行自由度的选择。3个准则函数常用于决定VAR模型的阶数。
模型的3个准则为:
(4)
(5)
(6)
其中T为样本数,
为模型残差的协差阵
的极大似然估计。
2.3.2. 系数矩阵估计
最小二乘法常被用来估计VAR模型的参数。即式(7)所示的估计值:
(7)
其中
是一个
维向量。
2.4. 模型评估准则
我们将本文提出的方法与G-O模型以及时间序列ARIMA模型进行对比评估。选取广泛应用于评估模型拟合优度的均方误差(MSE),模型的MSE定义为:
(8)
和
分别为实际值与估计值。此外,我们使用
指标来衡量相对预测精度的提高,该指标定义为:
(9)
(10)
其中
和
以及
分别表示本文提出的方法、ARIMA方法和G-O模型所产生的MSE值。
3. 案例分析
3.1. 数据介绍
3.1.1. 数据集1
论文选取两组数据并展开实验研究,各组件故障数据均来源于用户缺陷跟踪系统。数据集1为Kernel软件的时间序列数据。
软件是操作系统的核心。本文选用数据集包括input Devices、video、Bluetooth以及Network四个组件在2013年1月~2022年8月的故障数据,其中前104组数据用于训练模型,105~116组的故障数据用于预测。input Devices、video、Bluetooth以及Network四个组件分别用
表示具体数据见表1:

Table 1. Component failure data for Kernel
表1. Kernel的组件故障数据
3.1.2. 数据集2
数据集2为
软件2009年1月~2022年8月的三个组件的故障数据,将前150组数据划分为训练集;剩余14组数据为测试集用于验证模型。
是
中的一种以
进行数据库管理工作的KDE 4数据库接口。数据集2包含三个组件,组件名称分别为
以及
,在本文中用
以及
表示,如表2所列:

Table 2. Component failure data for Akonadi
表2. Akonadi的组件故障数据
3.2. 参数估计结果
3.2.1. 数据集1结果
在构建VAR模型之前,给定的时间序列数据应该满足平稳性的基本假设。本文采用ADF (Augmented Dickey-Fuller test)检验,得出p值为0.01,在显著性水平为0.05的情况下认为数据是平稳的。根据表3所示结果,参考AIC准则、BIC准则及HQ准则等统计量,最终选择的VAR模型最优滞后阶数为1阶。
因此对Kernel软件的四个组件input Devices、video、Bluetooth以及Network建立VAR (1)模型,通过参数估计得到拟合VAR模型如下:
(11)
3.2.2. 数据集2结果
经检验数据集2满足平稳性条件,根据表4所示,选择的VAR模型最优滞后阶数为1阶。
因此对软件
的三个组件general、IMAP以及server建立VAR (1)模型,通过参数估计得到拟合VAR模型如下:
(12)
3.3. 模型性能对比分析
3.3.1. 训练集数据模型对比
通过3.2节建立的模型,使用第3.1节中提出的实际数据的训练集数据部分,我们得到了表5中模型的均方误差(MSE)和相对精度
。在数据集1中,对比G-O模型,VAR模型虽在组件
与
上的拟合效果略低,但VAR模型综合
比G-O模型的综合
小,这说明VAR模型的整体拟合误差小,且其相对精度提高了42.23%。在数据集2中,VAR模型与G-O模型的平均均方误差分别为68.98与70.39,相对精度提高了6.038%。
对比ARIMA模型,在数据集1中可知VAR模型在
以及
两个组件拟合的MSE值略大于ARIMA模型,但在数据集1中VAR模型相较于ARIMA模型相对精度提高了30.88%,即在数据集1中两个模型各有优势;然而,从整体拟合效果来看,VAR模型综合
比ARIMA模型的综合
小,这说明VAR模型的整体拟合误差小。而在数据集2中VAR模型除组件
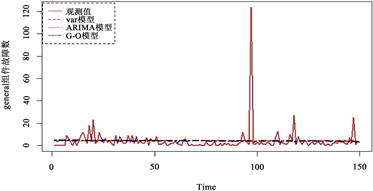
的均方误差略低于ARIMA模型外,相对精度提高了1.299%。总体来说,G-O模型拟合效果最差,VAR模型与ARIMA模型对各组件故障数据的拟合各有优势,但从总体来说VAR模型更有优势。图1和图2分别给出了两个数据集中各个组件VAR模型、ARIMA模型和G-O模型的月度故障数据的拟合图。

Table 5. MSE and R A I M S E values of the three models in the training set
表5. 训练集三种模型的MSE与
值
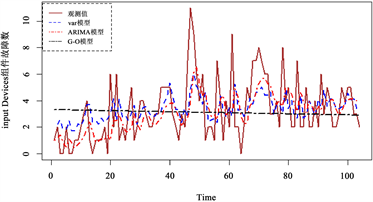 (a)
(a) 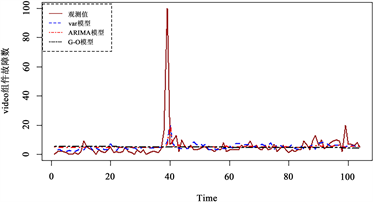 (b)
(b) 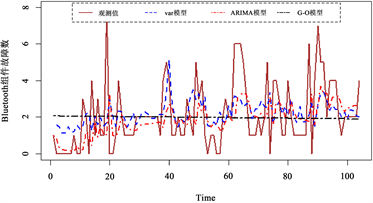 (c)
(c) 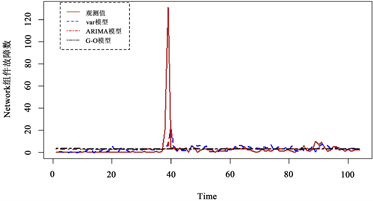 (d)
(d)
Figure 1. Fitting plot of the number of component failures for data set 1
图1. 数据集1组件故障数拟合图
3.3.2. 测试集数据对比
对划分为测试集的月份使用上文建立的模型进行预测,并与测试集原始数据进行对比,得到两个数据集的MSE值,如表6所示。从表中可以看出,本文所提方法所给出的MSE值平均比ARIMA模型分别低1.076%与12.418%,比G-O模型分别低37.893%和18.176%,这意味着本文方法提供了更准确的预测。图3和图4分别为两个数据集的VAR模型预测图。
 (a)
(a) 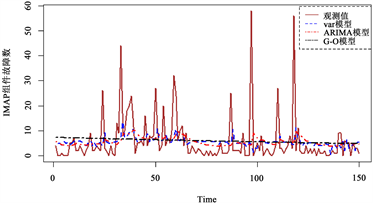 (b)
(b)  (c)
(c)
Figure 2. Fitting plot of the number of component failures for data set 2
图2. 数据集2组件故障数拟合图

Table 6. MSE and R A I M S E values of the three models in the test set
表6. 测试集三种模型的MSE与
值
4. 总结
软件的可靠性直接或间接取决于许多因素,并随着时间的推移而有很大的变化。现代软件可靠性的变化特征很难用传统的方式来全面描述,而且软件可靠性估计结果的差异性也比较大。基于对当前软件
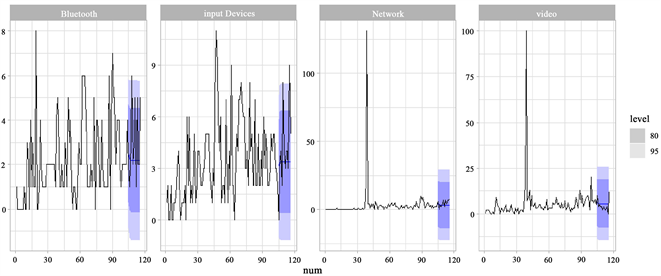
Figure 3. Prediction plots for dataset 1
图3. 数据集1的预测图

Figure 4. Prediction plots for dataset 2
图4. 数据集2的预测图
可靠性变化特征的分析,采用向量自回归VAR模型来拟合各软件组件的故障数据,建立预测模型。利用相同的数据,在相同环境下与传统的G-O模型和ARIMA时间序列模型进行了比较;结果表明,这种方法提高了软件可靠性预测的准确性,是一种优秀的软件可靠性预测方法。
基金项目
国家自然科学基金资助项目(71901078);贵州省电力大数据重点实验室(黔科合计Z字[2015] 4001)。
NOTES
*通讯作者。