1. 光电效应的回顾
光电现象由德国物理学家赫兹于1887年发现。根据有关资料 [1] [2],勒纳德在1902年对光电效应做了许多实验,由实验得出,发射的电子数正比于入射光所带能量;电子的速度和动能与发射的电子数目无关,而只与光的波长有关,波长减少,动能增加;每一种金属对应一特定频率,当入射光小于这一频率时,不发生光电效应。由此,他提出触发假说,假设在电子的发射过程中,光只起触发作用,电子原本就是以某一速度在原子内部运动,当光照射到原子上,只要光的频率与电子本身的振动频率一致,就发生共振,电子就以其自身的速度从原子内部逸出。勒纳德认为,原子里电子的振动频率是特定的,只有频率合适的光才能起触发作用。但是精确的实验证明,光电效应起因于能量转移。
根据有关资料 [3] [4],爱因斯坦在1905年提出光电效应的粒子解释。按照粒子说,光是由一份一份不连续的光子组成,当某一光子照射到对光灵敏的物质上时,它的能量可以被该物质中的某个电子全部吸收。电子吸收光子的能量后,动能立刻增加;如果动能增大到足以克服原子核对它的引力,就能在十亿分之一秒时间内飞逸出金属表面,成为光电子,形成光电流。单位时间内,入射光子的数量愈大,飞逸出的光电子就愈多,光电流也就愈强。爱因斯坦光电效应方程为:
,其中,Ek为电子的动能,h是普朗克常数,v是入射光子的频率,W0为逸出功,光电子逸出金属的频率临界值为截止频率,截止频率取决于金属材料,而发射电子的能量取决于光的波长,与光强度无关。
1916年,美国物理学者罗伯特·密立根用实验证实了爱因斯坦的理论是正确的,并且应用光电效应直接计算出普朗克常数。
光电效应分为光电子发射的外光电效应、光电导效应和光生伏特效应的内光电效应。
2. 光电材料的频谱曲线和经典光电效应解释中的问题 [5] - [11]
光电效应发现一百多年来,特别是近几十年,科技得到了飞速发展,光电效应已经渗透到许多方面,光敏材料已经有许多品种,光敏电阻是基于内光电效应的最常用的一种,我们看看它的光谱响应曲线。图1是光敏电阻的光谱响应曲线。
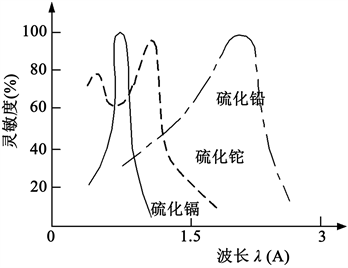
Figure 1. Spectral characteristic curve of photoresistor
图1. 光敏电阻的光谱特性曲线
我们可以从图上看出,不是光线的频率高于截至频率都能激发出光电效应,而当光线频率过高时,同低频一样同样不能发生光电效应。每一种光敏材料都有一个下截止频率、峰值频率和上截止频率。
图2是典型的光谱特性曲线,f0是峰值频率,fL、fH是通常情况下,定义的带宽,fmin是下截止频率,fmax是上截止频率。
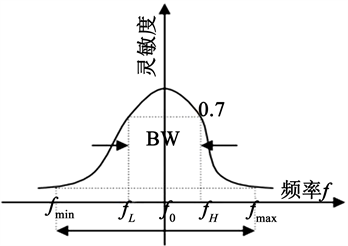
Figure 2. Typical spectral characteristic curve
图2. 典型光谱特性曲线
早在1902年,勒纳德通过实验指出“每一种金属对应一特定频率”,但是在爱因斯坦的光电效应解释中,只说明了下截止频率,忽视了“每一种金属对应一特定频率”的现象,也就是没有解释光电效应的峰值频率和上截止频率问题。
3. 电子的能级和共价电子
根据原子中电子的能级理论 [12],原子由原子核和围绕它的电子组成,电子分别位于不同能量的能级上运行,电子要在两个能级之间跃迁的前提是它要吸收或者释放能量,而且该能量还必须要和这两个能级之间的能量差一致。原子最外层电子为价电子。
图3是硫化锌 [13] 的原子结构示意图。图中Zn的原子序数是30,原子核外有30个电子,最外层有2个电子;S原子序数16,原子核外由16个电子,最外层有6个电子;在硫化锌形成晶体时,Zn的最外层2个电子和S的最外层6个电子形成共价电子,这时,这些价电子不再属于某一原子独有,而形成共有电子,这些共有电子运行形成一个等能面,设这个等能面的能量为Eg,这个等能面的能量大小应该与形成晶体的各种相邻原子之间对共价电子的库伦力有关,也与晶体结构有关。
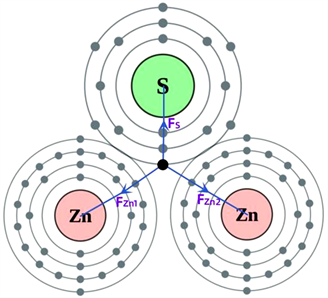
Figure 3. Atomic structure and covalent electrons of ZnS
图3. ZnS的原子结构和共价电子
硫化锌有两种晶体结构,一种是立方硫化锌晶体,一种是六方硫化锌晶体。图4是立方硫化锌晶体的示意图,又名闪锌矿,晶胞参数a为540.93 pm。立方硫化锌晶体中Zn原子个数为8 × 1/8 + 6 × 1/2 = 4,S原子个数为4,故立方硫化锌结构中,Zn原子与S原子个数比为4:4 = 1:1,所以立方硫化锌化学式为ZnS。一个立方硫化锌晶胞拥有4个“ZnS”微粒。Zn和S都是按四面体的方式成键,键型介于共价键与离子键之间。
在单独Zn原子中,价电子的库仑力势能为:
(1)
在单独S原子中,价电子的库仑力势能为:
(2)
上式中,qe是电子电量,
是Zn原子核带的电量,qS是S原子核带的电量,
是Zn原子序数,ZS是S子序数,
是价电子受到Zn原子核的库仑力势能,ES是价电子受到S原子核的库仑力势能。
是价电子到Zn原子核的距离,rS是价电子到S原子核的距离。
图3中,当硫化锌够成晶体时,共价电子运行到Zn原子和S原子中间时,共价电子将受到Zn原子和S原子的共同作用,受这个合力的作用,共价电子在Zn原子和S原子共同形成的势场中形成势能,组成等能面的一部分。此时,共价电子离Zn原子核和S原子核的距离有所变化,由于共价电子受到Zn原子核和S原子核的库仑力相互抵消,共价电子受到Zn原子核和S原子核库仑力的合力要远远小于电子单独在Zn原子核或者S原子核周围时的库仑力,共价电子受到总的库仑力势能也会远远小于单独在Zn原子核或者S原子核周围时的库仑力势能。在ZnS晶体中,实际上一个共价电子在任何位置都会受到相邻几个原子核的库仑力的共同作用,形成一个很复杂等能面。这时我们用等效原子序数Z*和等效半径r*表示,则有:
(3)
在半导体晶体中,还存在自由电子所在的等能面(相当于导带),在这个面上,电子受到各个原子的引力很小,只要晶体外加电压,自由电子便会单向运动,形成电流,外加电压高,单位时间通过的电子数多,电流大,外加电压低,单位时间通过的电子数少,电流小;自由电子等能面的自由电子数量受光照强度的限制,光照强度强,共价电子等能面跃迁到自由电子等能面的电子多,光照强度弱,共价电子等能面跃迁到自由电子等能面的电子少,在光照强度一定的情况下,共价电子等能面跃迁到自由电子等能面的电子数量一定。自由电子等能面的能量应该是一个很小的常数,我们记作E0。
和原子周围电子的能级一样,电子只能从一个能级跳跃到另一个能级。对于一个具体光敏材料,它的等价电子形成的等能面能量Eg是一个定值,当光敏材料受到适当频率光照时,等价电子获得能量将跳跃到自由电子能级层,这时:
(4)
式中,h为普朗克常数,f是光线的频率,λ是光线的波长,c是光速。这就是说:对于一个固定的光敏材料,在其固定的晶体结构下,它的共价电子会形成一个固定能量的等能面,当某一特定频率的光线照射光敏材料时,等能面上的电子获得的能量刚好能跳跃到自由电子能级,这样就形成了光敏材料的峰值频率。
在量子层面,我们无法描述每个电子的运行状态,只能用概率描述它的概率分布情况。对于接近峰值频率的光线,有部分电子可以跳跃形成自由电子,对于远离峰值频率的光线,电子跳跃的概率迅速下降,形成典型的光谱响应曲线(如图2)。
4. 结论
在光敏材料中,价电子的受力情况和光敏材料的晶体结构决定了光敏材料的价电子能级,当外界光线的光子能量hf和光敏材料的价电子能级与自由电子能级差相等时,光子能量传递给价电子,形成自由电子,对外光电效应的光敏材料,自由电子在外电场的作用下,逃离晶体形成光电子;对光电导效应的内光电效应材料,在外电压的作用下,形成电流。当外界光线的光子能量hf和光敏材料的价电子能级与自由电子能级差相差很大时,即使光线的频率再高,价电子也不能吸收光子能量,此时不能发生光电效应。