板栗去皮机的建模与有限元分析

Modeling and Finite Element Analysis of Chestnut Peeling Machine

摘要: 本文以板栗去皮机为例，利用SolidWorks对板栗去皮机进行三维建模并简化处理，然后导入Ansys Workbench软件，对板栗去皮机中重要部件：机架和螺旋送料机，进行静力学分析和模态分析，求解出机架和螺旋送料机的最大应力、变形量、固有频率和振型，结果表明：机架最大应力为：15.321 MPa，最大变形量为：1.7452 mm，前六阶固有频率范围：12.926~61.197 Hz；螺旋送料机最大应力为：1.7489 MPa，最大变形量：9.0035 mm，前六阶固有频率：39.525~131.77 Hz。机架和螺旋送料机最大应力均小于材料的屈服强度，机架由于质量大，前六阶固有频率均在100 Hz以内，并未发现机架和螺旋送料机存在共振频率。

Abstract: In this paper, the chestnut peeling machine is taken as an example. The three-dimensional model-ing and simplification of the chestnut peeling machine are carried out by SolidWorks, and then im-ported into Ansys Workbench software. The static analysis and modal analysis of the important parts of the chestnut peeling machine: frame and screw feeder are carried out. The maximum stress, deformation, natural frequency and vibration mode of the frame and screw feeder are solved. The results show that the maximum stress of the frame is 15.321 MPa, the maximum deformation is 1.7452 mm, and the first six natural frequencies range: 12.926~61.197 Hz; the maximum stress of the screw feeder is 1.7489 MPa, the maximum deformation is 9.0035 mm, and the first six natural frequencies are 39.525~131.77 Hz. The maximum stress of the frame and the screw feeder is less than the yield strength of the material. Due to the large mass of the frame, the first six natural fre-quencies are all within 100 Hz, and the resonance frequency of the frame and the screw feeder is not found.

1. 引言

机架是板栗去皮机中重要的支承部件，起支撑各个零部件的作用，螺旋送料机就安装在机架的顶部。板栗在输送过程中与螺旋叶片直接接触，产生相互作用力，机架和螺旋叶片产生振动，这个力是不断变化的，施加在螺旋叶片上是随机的激励，所以这就要求机架和螺旋叶片不仅要具有足够的静态刚度，还要具有良好的动态特性。马士龙 [1] 对板栗剥壳机的刀具等特关键部位特殊设计，可满足于不同成熟度和不同尺寸的板栗剥壳，在节省加工成本同时降低了能耗、提高了效率；丁彬 [2] 等人研究机械脱壳对不同荚果类型花生剥壳效果的影响，结果表明不同类型花生荚果机械剥壳差异较大；杨晓成 [3] 等人设计了一种花生低损剥壳装置，样机损伤率为1.26%，剥净率为98.89%，性能指标均优于国家标准。

传统的板栗去皮机的设计一般采用经验设计，其设计参数对低阶固有频率影响的动态特性分析和安全性未考虑，为了避免在工作过程中由于共振而引起的机械元件的损坏，需要计算零部件的模态频率和振型 [4] 。

2. 机架和螺旋送料机模型的构建和简化

SolidWorks焊件模块主要用于型材类部件的整体搭建与设计，可以很好地解决建模过程、装配过程繁琐及装配过程中遇到部件“位置约束过定义”等建模问题，修改方便 [5] 。利用Ansys Workbench进行有限元分析时，通常可以省略模型中对结构性能影响很小的特征和零件，使模型尽量简化，减小系统计算量 [6] 。根据机架和螺旋送料机的设计参数，在SolidWorks软件中建立三维模型，如图1、图2。再利用SolidWorks与Ansys Workbench的接口功能，将模型导入Ansys Workbench中进行静力学分析和模态分析 [7] 。

3. 静力学分析

3.1. 机架的静力学分析

作为ANSYS有限元分析模拟中重要的环节，网格划分要综合考虑计算量的大小和计算结果精度这两个因素，在权衡这两个方面后再确定网格的数量，在不影响计算结果精度的前提下，由于三维模型尺寸太大，网格划分的太密影响观感，所以机架的重要面采取40 mm的网格尺寸作为划分，其余面采用50 mm网格尺寸划分。螺旋送料机的叶片采用30 mm网格划分，其余面采用50 mm网格尺寸划分，单元数量为86,642个，节点数量为171,088个。

Figure 1. Three-dimensional model of frame

图1. 机架三维模型

Figure 2. Three-dimensional model of screw feeder

图2. 螺旋送料机三维模型

将机架三维模型导入Ansys Workbench中，对机架的底部进行固定约束，并对机架施加自身的重力以及1000 N的载荷，载荷是根据安装在机架上的零件重量以及板栗重量估计而来的。机架材料选择结构钢，材料的各项参数见表1。

Table 1. Material parameters

表1. 材料参数

从图3、图4可以看出，在对机架施加自身重力以及相应作用力条件下，最大变形量为0.98928 mm，应力发生在侧板位置，产生应力集中，最大应力为15.321 MPa，掏空的部分用来安装电动机的。

3.2. 螺旋送料机的静力学分析

螺旋送料机的材料选择为Q235，弹性模量、泊松比和密度等参数见表1 [8] ，考虑到螺旋送料机的尺寸太大，以及计算量的大小，所以螺旋轴的网格精度为50 mm，螺旋叶片的网格精度为30 mm，单元数量为6048个，节点数量为43,885个。

Figure 3. Deformation cloud of the frame

图3. 机架的变形云图

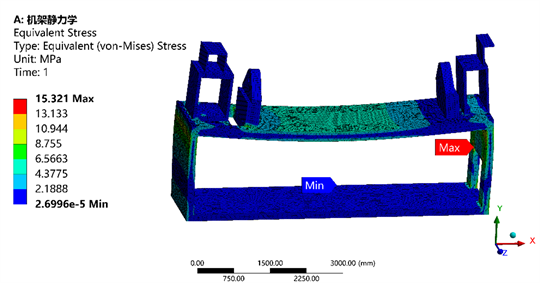
Figure 4. The stress cloud of the frame

图4. 机架的应力云图

将螺旋送料机的三维模型导入Ansys Workbench中，对其的两端施加约束，并对螺旋送料机施加自身的重力以及200 N的载荷，载荷根据一次进料板栗重量估计而来的。

从图5、图6可以看出，在对螺旋送料机施加自身重力以及相应作用力条件下，最大变形量为0.19853 mm，发生在螺旋轴的中间部位；由于应力集中，最大应力为12.927 MPa，发生在螺旋轴头部位置。

4. 模态分析

由于板栗去皮机在加工时，物料会与机架和螺旋刀片发生碰撞，振动幅度大，可能产生共振现象破坏机器。因此对螺旋送料机和机架进行模态分析是很有必要的，设计时可以规避掉共振频率。

模态分析(Modal Analysis)就是指通过计算和实验分析来获取机器设备所特有的振动特征的分析试验过程。经过模态分析就可以求得机器设备在哪个或者哪些频率域内容易受到干扰，得到这些数据就可以在设计或者实际生产中，尽量规避掉这些频率下的外部激励。模态是指机械结构的固有振动特性，每一个模态都有特定的固有频率、阻尼比和模态振型。分析这些模态参数的过程称为模态分析。按计算方法，模态分析可分为计算模态分析和试验模态分析。

模态分析在Ansys有限元分析中是计算结构振动特性的数值技术，是动力学分析的基础，是求解物体的固有特性，主要是频率和振型，当物体达到固有频率时，物体震动的振幅会变得很大，宏观上展现出来是震动大，一般都会影响正常使用。模态分析使用的材料属性仅需要弹性模量和泊松比。

Figure 5. Deformation cloud of screw feeder

图5. 螺旋送料机的变形云图

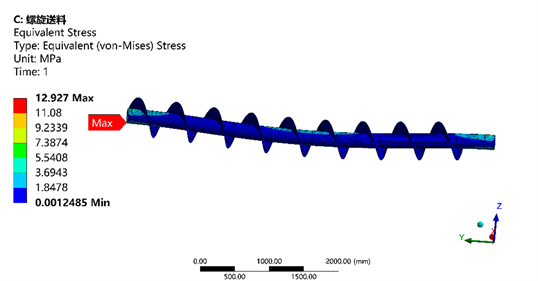
Figure 6. Stress cloud diagram of screw feeder

图6. 螺旋送料机的应力云图

模态分析可以帮助设计人员确定结构的频率和振型，在设计上有效规避共振。模态分析的最终目标是识别出系统的模态参书，为结构系统的振动特性分析、震动故障诊断和预报以及结构动力特性的优化设计提供依据。

4.1. 模态分析理论

模态分析的基础是以模型的数值计算为依据，最终实质是求解有限数量自由度的无阻尼线弹性系统运动方程，其矩阵式可由以下公式推导得来 [9] 。

经典力学中物体的动力学通用方程为：

(1)

式中：

[M]为质量矩阵；

[C]为阻尼矩阵；

[K]为结构刚度矩阵；

$\left\{\ddot{u}\right\}$ 为位移矢量；

$\left\{\stackrel{\dot{}}{u}\right\}$ 为点速度矢量；

$\left\{u\right\}$ 为点加速度矢量；

$F\left(t\right)$ 为随时间变化的载荷函数。

不同的分析类型会求解不同的运动方程式，在模态分析中， $\left\{F\left(t\right)\right\}=0$ ，结构阻尼矩阵[C]通常忽略。在谐响应分析中， $F\left(t\right)$ 和 $u\left(t\right)$ 都为谐函数。

无阻尼模态分析的动力学运动方程为

$\left[M\right]\left\{\ddot{u}\right\}+\left[K\right]\left\{u\right\}=0$ (2)

当发生谐振动时方程为

$\left(\left[K\right]-{\omega }_i^2\left[M\right]\right)\left\{{\Phi }_i\right\}=0$ (3)

因此，对于任意零部件的模态分析，其固有圆周频率 ${\omega }_i$ 和振型 ${\Phi }_i$ 均可得出。

有预应力模态分析用于计算有预应力结构的固有频率和模态，其需要两个迭代过程。首先要通过静力分析把预应力添加到结构相应位置处，进行静力分析。

$\left[K\right]\left\{x_0\right\}=\left\{F\right\}$ (4)

基于静态分析的应力状态，应力刚度矩阵[S]用于计算结构分析。

$\left[{\sigma }_0\right]\to \left[S\right]$ (5)

其次求解预应力模态分析，原来的模态分析方程包括了[S]阵。

$\left(\left[K+S\right]-{\omega }_i^2\left[M\right]\right)\left\{{\Phi }_i\right\}=0$ (6)

4.2. 机架的模态分析

用模态分析可以确定一个结构的固有频率和振型，固有频率和振型是承受动态载荷结构设计中的重要参数。根据模态分析理论可知，机架的结构振动特性与其自身的刚度和质量有关，与外力无关，因此模态分析过程不考虑外载荷及边界条件。

机架结构容易受到低阶振动的影响，分析机架结构的前六阶模态。低阶固有频率比较低，低阶的模态刚度也比较低，在同样量级的激励作用下，前几阶低阶响应所占用的权值较大。所以，在对研究对象进行模态分析时，对其运动响应起主导作用的是前几阶。因此，对机架和螺旋送料机进行模态分析时只提取了其前六阶的固有频率和模态振型，见表2，和相应的振型云图，见图7。

Table 2. The first six natural frequencies and modal shapes of the frame

表2. 机架前六阶固有频率和模态振型

从图7可以看出，机架最小固有频率为12.926 Hz，最大固有频率为61.197 Hz，其中5阶模态当固有频率为49.186 Hz时，机架上底板变形达到最大值，变形值为1.7452 mm，4阶模态当固有频率为43.482 Hz时，机架上底板变形值最小，变形值为0.3133 mm。

(a) 1阶振型 (b) 2阶振型 (c) 3阶振型 (d) 4阶振型 (e) 5阶振型 (f) 6阶振型

Figure 7. Frame first 6 order modal shape figure

图7. 机架前6阶模态振型图

4.3. 螺旋送料机的模态分析

螺旋送料机的材料选择Q235，弹性模量为2.06 × 10⁵ MPa，泊松比为0.25。选取螺旋送料机的前6阶模态，并对其进行分析。前六阶的固有频率和模态振型，分别见表3和图8。

分析表3可以知道，螺旋送料机主要的振型是弯曲、摆动和扭转。前6阶频率最大为131.11 Hz，最小为40.14 Hz。频率随阶数的增加而增加，这符合模态分析无阻尼振动的随机性。

(a) 1阶振型 (b) 2阶振型 (c) 3阶振型 (d) 4阶振型 (e) 5阶振型 (f) 6阶振型

Figure 8. The first 6 order modal shape diagram of screw feeder

图8. 螺旋送料机前6阶模态振型图

Table 3. The first six natural frequencies and modal shapes of screw feeder

表3. 螺旋送料机前六阶固有频率和模态振型

分析图8可知，螺旋送料机的1阶振型主要是螺旋轴中间部位沿z轴上下弯曲振动，最大变形为2.3817 mm；2阶振型主要是螺旋轴中间部位沿z轴上下弯曲振动，最大变形量为2.3845 mm；3阶振型主要是螺旋轴整体沿z轴上下震荡弯曲变形，最大变形量为2.2791 mm；4阶振型主要是螺旋轴沿着x和z轴的合方向弯曲变形，最大变形量为2.3308 mm；5阶振型主要是螺旋轴沿y轴扭转变形，最大变形量为6.4674 mm；6阶振型主要是螺旋轴沿y轴扭转变形，最大变形量为8.934 mm。

分析可得，第6阶振型变形量最大为8.934 mm，固有频率为131.11 Hz。

5. 结论

通过Ansys Workbench静力学分析可知，机架的最大应力为15.321 MPa，远远小于结构钢的屈服强度；螺旋送料机的最大应力为12.927 MPa，也远远小于材料Q235的屈服强度，满足材料使用特性。通过模态分析可知，机架的第5阶振型变形量最大为1.7452 mm，固有频率为49.186 Hz；螺旋送料机的第6阶振型变形量最大为8.934 mm，固有频率为131.11 Hz。从仿真结果来看，两者没有相同频率，不会发生结构共振。在实际工作当中，可以通过调整电机的功率来控制激励频率，规避机架和螺旋送料机的固有频率。