1. 引言
随着通信技术的发展,通信的传输内容不再局限于单一的文本和语音消息,更多的是内容丰富、信息量大的图像信息 [1] 。由于图像数据量大、冗余度高,在图像的传输过程中,极易受到攻击和窃取,传统图像加密算法的安全性已经不能满足现今的传输需求。
由于混沌系统具有遍历性、伪随机性、初值敏感性等 [2] ,能产生随机性强且难以预测的混沌序列,因此在图像加密方面具有独特的优势。2016年Zhou [3] 等人提出了一种基于超混沌系统和二维压缩感知的图像压缩加密方案,但由于采用的是低维的混沌系统,导致其密钥空间较小仅为2149,容易被暴力破解。
2021年,张雷 [4] 等人提出了一种结合 S 盒与混沌映射的图像加密算法,但仍采用经典的Logistic 混沌映射和超混沌chen映射,并未使用新的混沌系统。现在,越来越多的学者结合DNA编码,提出新的图像加密算法。2017年Wang [5] 等人通过扫描平面图像,对图像中的特定行采用混沌映射控制的DNA编码,最终生成密钥图像。但现有DNA图像加密算法,多数借助混沌系统打乱DNA编码,然后通过对行、列或像素点进行置换,从而实现图像加密。然而Wei [6] 等人指出,仅通过置换算法和DNA编码实现图像加密的安全性较低。
自忆阻器被发现以来 [7] [8] ,由于其具有良好的非线性特性和记忆性,在混沌电路、神经网络、类脑计算等方面得到应用。包伯成 [9] 等人通过将蔡氏电路中的非线性电阻替换成理想的忆阻器模型,发现了具有极端多稳定性的忆阻电路。Ding [10] 等人用通量控制忆阻器来模拟电磁感应效应,并结合PWL函数模拟双曲正切函数的特性,建立了一个双神经元的忆阻PWL-HNN模型。文献 [11] [12] [13] 通过添加或替换电路中的非线性器件构造了许多具有丰富动力学行为的混沌系统。虽然忆阻器具有广泛的应用前景,但在图像加密领域,使用含忆阻混沌系统的加密算法并不多见。
针对低维混沌系统密钥空间小,传统加密算法安全性低等缺点,本文在lv混沌系统的基础上,将磁控忆阻器作为负反馈项添加到原系统,构建了一个含忆阻的新四维混沌系统。分析了系统的耗散性、Lyapunov指数和维数、分岔图等,并通过电路仿真软件,对系统电路进行仿真。最后借助该混沌系统生成伪随机序列,对明文图像进行两次扩散和一次置乱,实现对图像的加密。结果表明,使用本文混沌系统构建的图像加密算法密钥空间比低维混沌系统有较大的提升,并且加密效率高,有较高的安全性。
2. 四维忆阻混沌系统构建
吕金虎 [14] 等人提出了一个新的三维混沌系统,式(1)是lv混沌系统的数学模型:
(1)
在lv系统的基础上,通过添加式(2)的磁控忆阻器作为负反馈项到式(1)中,从而构建新的四维混沌系统,其中m和n为忆阻器状态参数。
(2)
式(3)为新系统的数学模型,式中x,y,z,w是系统的四个状态变量。a、b、c、e为系统参数。
(3)
使用龙格–库塔方法 [10] 对式(3)进行仿真,设置系统参数
,
,
,
,
,
仿真步长为0.01,仿真时间为4000秒,状态变量的初值
,系统的相图如图1所示。从相图中可以看出,新系统呈现双涡卷吸引子。
 (a)
(a) 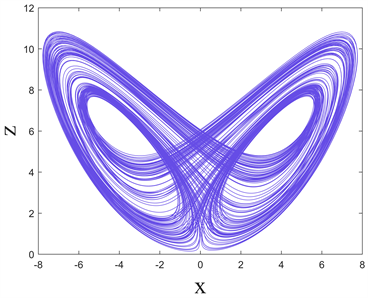 (b)
(b)  (c)
(c)  (d)
(d)
Figure 1. Phase portraits of chaotic attractor (a) x-y plane; (b) x-z plane; (c) y-z plane; (d) x-w plane
图1. 混沌吸引子各平面相图(a) x-y平面;(b) x-z平面;(c) y-z平面;(d) x-w平面
3. 系统非线性特性分析
3.1. 耗散性分析
对新的系统(3)进行耗散性分析
(4)
无论w取何值,
,因此系统(2)是耗散的,且以指数
的速率收敛,当
时,系统中的任一体积元将收敛到0。
3.2. 平衡点及稳定性分析
固定系统参数不变,令新系统的左边等于0,即式(5):
(5)
通过求解,可得该混沌系统共有4个平衡点:
,
,
,
。
其中α为任意实数,因此
为线平衡点,在平衡点处对系统(2)线性化,得到系统的Jacobi矩阵如下:
(6)
对于线平衡点
,其特征方程如式(7)所示:
(7)
四个特征根分别为
,
,
,
,带入参数后求得
,
,
,
,
的值与
有关,当
时,
,此时稳定点的类型为指标1的鞍点。当
或
时,此时稳定点的类型为稳定结点。
平衡点S1~S4的特征根如表1所示:

Table 1. Characteristic roots and types of equilibrium points
表1. 各平衡点的特征根与平衡点类型
3.3. 动力学分析
3.3.1. 初值敏感性
对于系统(3),为分析系统对初值的敏感性,对初值
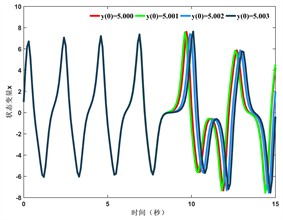
添加微小扰动,并观察新初值下状态变量的动态轨迹。从图2中可以看出,状态变量在7秒后动态轨迹不再重合,随着时间推移,不同初值下的轨迹差异逐渐变大,说明系统的初值敏感性较好。
 (a)
(a)  (b)
(b) 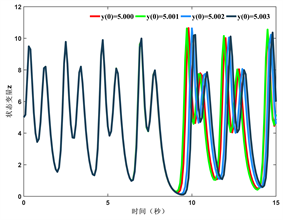 (c)
(c) 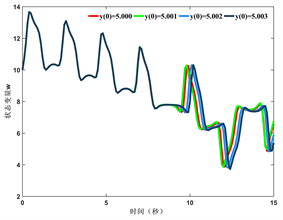 (d)
(d)
Figure 2. Dynamic trajectory of state variable when initial value changes slightly (a) Variable x; (b) Variable y; (c) Variable z; (d) Variable w
图2. 初值微小变化时状态变量动态轨迹 (a) 变量x;(b) 变量y;(c) 变量z;(d) 变量w
3.3.2. 李雅普诺夫指数和维数
固定系统参数和系统初值不变,利用Wolf [10] 算法求得系统的4个李雅普诺夫(Lyapunov Exponent, LE)指数分别为:
,
,
,
。系统具有两个大于0的Lyapunov指数
和
,系统表现出超混沌状态。系统的分数维如式(8)所示:
(8)
3.3.3. 随参数e分岔图
为分析系统随参数e变化的系统特征,设置系统(2)初值
,固定其他参数不变,通过仿真得到系统在参数e变化下的分岔图以及Lyapunov指数图。可以观察到随参数e的变化,系统由周期进入混沌的路径。当
时,最大的LE指数大于0,说明系统处于混沌状态。其中
时,
和
均大于0,此时系统处于超混沌状态,当
和
时,4个LE指数均小于0,混沌状态消失。
下面在固定参数
条件下,讨论系统(2)随参数e变化的系统特征。
 (a)
(a) (b)
(b)
Figure 3. Chaotic dynamics varying with parameterse (a) Bifurcation diagram; (b) Lyapunov exponential spectra
图3. 随参数e变化的混沌动力学 (a) 分岔图;(b) Lyapunov指数图
固定其他系统参数不变,取参数
时,通过观察图3的分岔图及Lyapunov指数图并结合图4(a)和图4(b)可知,在此参数下,系统为周期一状态。取参数
。从图3以及图4(c)和图4(d)可知,在此参数下,系统处于周期二状态。取参数
,从图3以及图4(e)和图4(f)可知,在此参数下,系统处于混沌态。取参数
,从图3以及图4(g)和图4(h)可知,在此参数下,系统为拟周期态。取参数
,从图3以及图4(i)和图4(j)可知,系统为超混沌态。
4. 电路实现与仿真
为验证所设计混沌系统的电路可行性,选用电阻、电容、乘法器和TL082CP运算放大器等电路元件,在版本为14.0的Multisim软件中进行仿真。对原系统进行压缩变换,令
,
,
,
,将系统转化为式(9):
(9)
对系统进行时间尺度变换,使电路参数能更好的与系统匹配,令
,其中尺度变换因子
,则系统经过时间尺度变换可转化为式(10):
(10)
根据基尔霍夫定律得到式(10)的电路方程为:
(11)
其中
,均为10 nF,
,选择系统参数
,
,
,
,
,
时,可求得
,
,
,
,
,
,
。
系统的电路模型如图5所示:
通过模块化设计并在Multisim软件上进行仿真验证,从示波器观察到的相图如图6所示。电路仿真结果与Matlab数值仿真结果相一致,从而证明系统的物理可实现性。
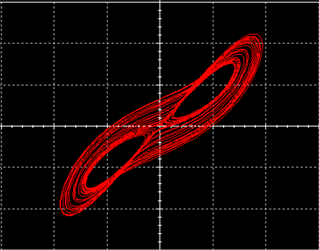 (a)
(a)  (b)
(b)  (c)
(c)  (d)
(d)
Figure 6. Circuit Simulation result (a) x-y plane; (b) x-z plane; (c) y-z plane; (d) x-w plane
图6. 电路仿真结果(a) x-y相图;(b) x-z相图;(c) y-z相图;(d) x-w相图
5. 新混沌系统在图像加密中的应用
采用明文关联的置乱加密算法 [15] ,将所设计的混沌系统应用到图像加密中,加密过程如图7所示。
明文图像经过混沌密码发生器与密钥结合,最终生成密文图像。在混沌密码发生器中,明文图像经过两次扩散和一次置乱,其中置乱算法与明文相关联。
5.1. 混沌密码发生器
通过本文设计的混沌系统来生成6个大小为
的伪随机矩阵X、Y、Z、W、U和V。密钥
,其中
、
、
、
是混沌系统的状态初值,
,
是随机数。设置混沌系统的状态初值为密钥K中的
、
、
、
,经过
次迭代,从而跳过混沌系统的过渡态,然后继续迭代MN次,得到
、
、
、
4个伪随机矩阵,最后通过式(12)生成X、Y、Z、W、U和V共6个矩阵。式中
,
。
(12)
5.2. 加密算法
明文图像P的大小为
,借助密码发生器生成的伪随机矩阵
,将明文图像转换为新的矩阵
(13)
其中
,
,
是密码发生器中用来跳过混沌系统过渡态的随机数。
步骤一:令
(14)
将
转换为
,若
,则重复步骤一,否则令
,
,当
时
(15)
直到
时,完成明文图像的第一次扩散得到新的图像A。
为了抹除图像中相邻像素点的相关性,对扩散后的图像A进行置乱,得到置乱后的图像B。置乱过程如下:
(16)
(17)
如果
或
,
或
,
,
时原像素点位置不变。否则
与
互换位置。对图像A中的像素点,按从左到右、从上到下的顺序遍历置乱步骤,最终得到新的置乱图像B。
步骤三:借助矩阵Y对置乱图像B中的像素点进行扩散,其扩散过程为从最后一个像素点向前进行扩散,从而将图像B转换为矩阵C,扩散过程如下:
Step1:令
,
,将
转换为
。
(18)
Step2:令
,将
转换为
(19)
若
,重复Step2。否则
,
。如果
(20)
并重复Step2。当
时,完成对图像B的扩散,此时的矩阵
即为密文图像。
6. 图像加解密仿真及安全性能分析
6.1. 图像加解密仿真结果
使用分辨率为512 × 512的Lena和Baboon图像进行图像加解密仿真实验,混沌系统为与电路仿真系统一致的系统(2)。为不失一般性,设置密钥K = [13 48.58 −15.11 22 98 456]对图像进行加密,算法仿真结果如图8所示。
6.2. 直方图分析
像灰度级像素的数目通常用直方图来描述 [16] 。如果攻击者窃取了密文图像,就有可能通过分析密文图像的直方图来提取密文图像中的信息。因此,良好的加密算法,密文的直方图应均匀分布。图9显示了原图像与密文的分布直方图,从图中可以看出,与原图像直方图相比较,加密图像的直方图分布均匀,绝大部分统计信息被抹除,从而使得加密图像能有效地抵抗统计攻击。
 (a)
(a)  (b)
(b)  (c)
(c)  (d)
(d)
Figure 9. Original image and Ciphertext histogram (a) Lena original image; (b) Ciphertext histogram; (c) Baboonoriginal image; (d) Ciphertext histogram
图9. 原图与密文直方图(a) Lena;(b) 密文直方图;(c) Baboon;(d) 密文直方图
6.3. 信息熵分析
信息熵 [17] 反映了图像信息的不确定性,信息熵越大,图像的信息量越大,所含的可获得信息越少,计算公式如式(21)所示。
(21)
其中
表示灰度值i出现的概率,L表示图像的灰度等级,对于灰度等级为256的灰度随机图像,信息熵的理论值为8,越接近理论值,图像的可视信息越少,表2给出了不同算法的信息熵。

Table 2. Information entropy of different algorithms
表2. 不同算法的信息熵
从表2中可以看出,本文算法的信息熵接近于理论值,优于超混沌Lorenz加密算法,且优于文献 [15] 所使用的DNA加密算法。
6.4. 密钥空间分析
通常密钥空间越大,抵御穷举攻击的能力越强,加密图像的安全性越好 [20] 。本文的密钥K = [13 48.58 −15.11 22 98 456],
、
、
、
是混沌系统的初值,精度均可达到10−15,
,
是跳过混沌过渡态的迭代次数,值为0到2048,步长为1的整数。因此密钥空间的容量可达到2147远大于2100,能有效抵御穷举攻击。表3给出了不同算法的密钥空间。

Table 3. Key Spaces for different algorithms
表3. 不同算法的密钥空间
从表3中可以看出,本文的密钥空间比传统超混沌Lorenz算法提升了234,优于文献18中的神经网络算法。
6.5. 相关系数分析
明文图像相邻的像素点通常具有很强的相关性,而加密图像水平、垂直、对角方向上相邻像素点间的相关性理论上为0,也即各像素点间不具有相关性。统计本文与其他文献中Lena图像与加密图像在不同方向上的相关性,结果如表4所示。

Table 4. Plaintext and ciphertext pixel correlation
表4. 明文与密文像素相关性
从表4中可以看出,本文相邻系数相关性的表现比传统超混沌Lorenz算法有较大的提升。
6.6. 差分攻击分析
差分攻击是一种选择明文攻击,通过分析明文图像差对密文图像差的影响,从而获取加密密钥的一种攻击方式。往往通过定量分析像素改变率(NPCR) [22] 和归一化像素平均变化强度(UACI) [22] 来度量图像加密算法对差分攻击的抵抗能力。
对于两幅随机图像,同一位置像素点不相同的概率为99.61%,由于像素点位置的任意性,NPCR的理论值为99.61%。由于NPCR衡量图像差异性时较为片面,通常还需结合UACI共同分析,UACI通过计算相应位置的像素变化强度来评价图像的差异性,其理论值约为33.46%。公式如下:
(22)
(23)
式中,P1,P2是两幅大小为
的图像,当
时,
,否则
。本文通过加密Lena图和改变任一像素点后的Lena图,得到两幅加密图像。重复一百次实验,并计算NPCR和UACI的平均值,如表5所示。

Table 5. Average NPCR and UACI of ciphertext images with different algorithms
表5. 不同算法密文图像平均NPCR和UACI
可以看出,本文算法的NPCR值和UACI值十分接近理论值,能有效抵御攻击。
7. 结论
本文通过添加忆阻器构建超混沌系统的方式,将磁控忆阻器添加到lv系统中,构建了一个新的具有丰富动力学行为和稳定平衡点的四维忆阻超混沌系统。此外,针对图像安全问题,将该系统与明文关联的图像加密算法结合,对明文像素点进行扩散,置乱再扩散,最终实现图像加密。最后,通过计算密钥空间大小,发现与传统超混沌Lorenz系统相比,密钥空间提高了234,像素点的相关系数有数量级的降低,安全性得到提高,可广泛应用于图像加密领域。
基金项目
贵州省自然科学基金项目(黔科合基础-ZK [2023]一般055);贵州大学人才基金(贵大人基合201615号)。
参考文献
NOTES
*通讯作者。