1. 引言
神经元和心肌细胞正常的电活动对人和动物来说很重要,当神经系统受到入侵和伤害时,大脑和心脏的崩溃会导致严重的疾病甚至死亡 [1] 。神经元作为神经系统的基本功能单位,能感受刺激和传导兴奋。神经元的电活动行为依赖于复杂的电生理活动,在不同的Ca2+、Na+、k+离子浓度以及外界电磁辐射下,神经元能表现出丰富的放电模式。近年来,大量学者 [2] [3] [4] [5] 已经研究了神经元的放电状态,例如,Hindmarsh-Rose神经元模型有效的表述神经元活动的主要特征,而且有更为可观的分岔参数;Lv等人 [6] 指出神经元中应考虑电磁感应的影响,因此在HR神经元模型中引入磁通量,用来描述神经元的记忆效应,用忆阻器实现磁通量和膜电位之间的耦合。
基于神经元模型,通过选取适当的噪声强度来刻画外界电磁辐射的强度,可以发生随机和相干共振有趣的现象 [7] [8] [9] [10] ,外界刺激电流强度可以诱发有节律的放电模式。此外,可以将不同类型的噪声引入到神经元模型中,例如文献 [11] 呈现的结果证实了HR模型存在噪声效应以及考虑离子通道效应。除此之外,还有文献 [12] 中,利用Levy噪声,研究了相噪声驱使改进的生物神经元模型相关问题。本文在Hindmarsh-Rose神经元模型中引入磁通,提出了一种新的模型,可以合理地讨论电磁感应和辐射对心肌细胞或神经元的影响。在此基础上,对改进后的模型又引入了外加电磁辐射,研究了神经元在电活动中的动力响应和模态跃迁。
2. 模型描述及其平衡点稳定性分析
加入磁通和外界电磁辐射的电磁场神经元模型描述如下:
(1)
变量
分别表示膜电位、恢复变量的慢电流、自适应电流、通过神经元的细胞膜的磁通和电流通过忆阻的电荷量。
表示神经元的外部交变刺激电流,其表达式描述为
。
表示反馈增益,忆阻器描述了电荷对磁通量的依赖性,其表示形式为:
基于法拉第电磁感应定律,
定义为当磁通量改变时膜电位上的反馈电流,其表示如下:
其中
是确定的参数。同时神经元由于忆阻器的引入而具有记忆效应,与生物实验中的磁性蛋白作用相对应,用来刻画外界刺激断开后反向电流产生的磁场。
定义为当外界变化电流刺激时磁通量的变化,
为荷控型忆阻器,其表达形式为:
的物理意义可以描述为如下形式:
其中
是确定的参数,此外,系统的参数
也是确定的参数,其值为:
。
为膜电位感应磁通量的变化。
是外加磁场,为简单起见,将其定义为类如
的周期性外加电磁辐射。此外,可以用高斯白噪声来刻画外部磁场的影响。
对于电磁场神经元模型(1)的平衡点
满足以下方程组:
(2)
将给定的参数代入方程组(2)可得该方程组的解为:
。
因此,系统的平衡点有如下四种情况:
取
,得到系统的一个平衡点
,系统(1)在该平衡点
处所对应雅克比矩阵的特征值为:
由特征值的正负性可得平衡点
是稳定的焦结点。类似的,令
,可得系统的另一个平衡点
,系统(1)在该平衡点
处所对应雅克比矩阵的特征值为:
同理可得平衡点
是鞍结点。在该系统中,平衡点的稳定性对应于神经元的放电模式,即在稳定的平衡点处神经元处于静息态,在不稳定的平衡点处神经元处于非静息放电模式。
下面讨论系统(1)的稳定性,经计算,系统(1)在平衡点
处的雅克比矩阵为:
其中
。其相对应的特征方程为:
(3)
其中
由Routh-Hurwitz判据可知
时,方程(3)的所以特征值都有负实部,所以系统(1)在平衡点
处是渐进稳定的。
3. 数值仿真
在数值仿真中,给定初值
,采用四阶Runge-Kutta方法,改进后的模型具有更多的分岔参数。通过选取不同的参数值,神经元产生不同的放电模式。当选择合适的外部电磁辐射强度时,给定反馈增益的值为
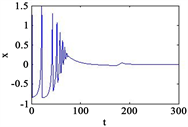
,电磁感应存在的情况下,通过增加跨膜电流可以得到电活动的多种放电模式。此外,考虑了跨膜电流角频率的影响,结果如图1所示。
 (a)
(a) 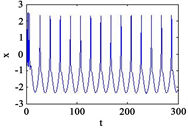 (b)
(b) 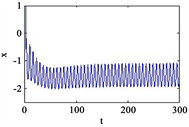 (c)
(c)  (d)
(d)
Figure 1. Time series of neuronal membrane potential under different intensities of stimulation current, external magnetic field
, external stimulation current
(a) A = 5, B = 0.004; (b) A = 5, B = 0.3; (c) A = 5, B = 0.8; (d) A = 5, B = 10
图1. 不同强度的刺激电流下神经元膜电位的时间序列,外界磁场
,外界刺激电流
(a) A = 5,B = 0.004;(b) A = 5,B = 0.3;(c) A = 5,B = 0.8;(d) A = 5,B = 10
由图1可知,随着角频率的增加,神经元的电活动可以呈现出多种放电模式,甚至在膜电位的时间序列中可以观察到混沌行为。广泛的数值结果表明通过设置改变角频率可以产生周期放电行为和尖峰放电行为。此外,通过改变角频率,从膜电位的时间序列中计算出ISIs,如图2所示。
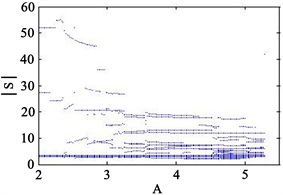
Figure 2. Bifurcation diagram of peak to peak interval (ISI) in membrane potential sequence with transmembrane current at
, where ISI represents the peak to peak interval in membrane potential sequence
图2. 在
时膜电位序列中的峰峰间隔(ISI)随跨膜电流变化的分岔图,ISI表示膜电位中的尖峰间隔
为了解电磁辐射的影响,采用周期性辐射来改变磁场分布和磁通量,因此外界电磁辐射描述为
,其中C和D分别表示振幅和频率。模型的参数为
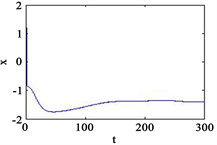
时,可以通过选取不同的参数值来去除神经元的静息态,此外,也可以通过外加周期信号来改变神经元的膜电位,其随时间变化的时间响应图如图3和图4所示。
 (a)
(a) 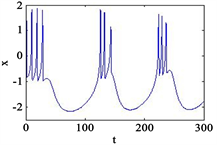 (b)
(b) 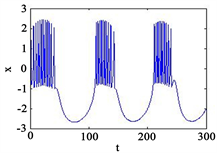 (c)
(c)  (d)
(d)
Figure 3. Time series of neuronal membrane potential under different intensities of stimulation current, external magnetic field
, External stimulation current
B = 0.02, (a) A = 0.02; (b) A = 1.2; (c) A = 5; (d) A = 40
图3. 不同强度的刺激电流下神经元膜电位的时间序列,外界磁场
,外界刺激电流
其中B = 0.02,(a) A = 0.02;(b) A = 1.2;(c) A = 5;(d) A = 40
对比图3和图4可得当外界周期信号的振幅大而频率较小时,神经元出现簇放电行为,当外界刺激电流的振幅较小时,神经元膜电位的时间序列主要由角频率决定,当外界刺激电流的振幅较大时更容易产生簇放电模式。
 (a)
(a)  (b)
(b)  (c)
(c)  (d)
(d)
Figure 4. Time series of neuronal membrane potential under different intensities of stimulation current, external magnetic field
, External stimulation current
A = 5, (a) B = 0; (b) B = 0.02; (c) B = 0.1; (d) B = 1
图4. 不同强度的刺激电流下神经元膜电位的时间序列,外界磁场
,外界刺激电流
其中A = 5,(a) B = 0;(b) B = 0.02;(c) B = 0.1;(d) B = 1
由外界磁场的不确定性,因此可以在系统(1)中通过引入电流产生外界磁场,即用高斯白噪音描述外界磁场的影响,其描述为
。在数值模拟中参数设置如下:
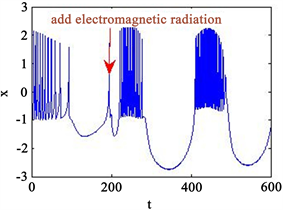
。实际上,选择适当的外界强度时,神经元可以产生类似簇放电以尖峰放电的放电行为。以上结果证明改进后的模型可以对外界刺激产生多种响应模式。图5说明了当神经元暴露在外界电磁辐射下时,神经元电活动可以由尖峰放电转化为多种放电行为。
总之,改进后的电磁场神经元模型由于拥有更多的分岔参数并且考虑了电磁感应以及电磁辐射的影响。电磁场神经元模型中用磁通来描述第四个变量,穿过细胞的磁通量是随外界磁场的变化而变化,因此电磁场可以通过周期函数以及高斯白噪音来刻画。广泛的数值模拟结果表明,在外界磁场作用下,通过调节参数可以观察到神经元的多种放电模式。
4. 总结
基于电磁感应定律,为了检测电磁辐射的影响,在三变量的HR模型的基础上引入磁通项,建立一个新的神经元模型。由于更多参数的引入,使得神经元的动力学行为更加复杂和有趣。讨论了周期性电磁辐射以及高斯白噪音下的神经元细胞不同模式的响应。结果表明当外界刺激振幅较大时更容易产生
 (a)
(a) 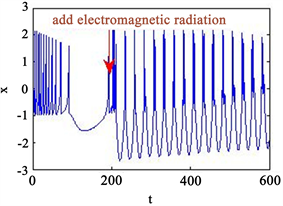 (b)
(b)
Figure 5. Time series of neuronal membrane potential under different intensities of electromagnetic radiation, external magnetic field
, External stimulation current
, A = 6, B = 0.01 (a) v = 0.001; (b) A = 0.01
图5. 不同强度电磁辐射下神经元膜电位的时间序列,外界磁场
,外界刺激电流
其中A = 6,B = 0.01 (a) v = 0.001;(b) A = 0.01
簇放电模式,也证实了神经元对外界刺激电流有一定的自适应性。这个模型有助于我们理解在电磁辐射作用下神经元对电活动模式的选择和转换,也有助于对噪声和电磁辐射下神经网络集体行为的进一步研究。
基金项目
2021年广东理工学院科技项目(自然科学) (2021GKJZK013)。
参考文献
NOTES
*通讯作者。