基于离散元理论的筒辊磨粉磨特性仿真分析

Simulation Analysis of Grinding Characteristics of Horomill Based on Discrete Element Theory

摘要: 随着粉磨设备呈现大型化、高效化、节能化的新趋势，利用数值模拟软件对磨机工况进行仿真分析，成为提高设计效率、降低设计成本和设计周期的常用方法。本文基于离散元软件EDEM采用控制变量法对φ2600筒辊磨的筒体转速、最小料层厚度、喂料量设置试验组进行仿真，从破碎率和能耗的角度分析磨机的粉磨特性，为磨机设计和运行参数选择提供参考。结果表明：转速越高，破碎率越高，转速高于42 rpm时粉磨单位能耗快速增加；最小料层厚度与破碎率呈负相关关系，单位能耗随之先降后升，合理取值范围为18~24 mm；喂料量在22~37 tph范围内，破碎率存在峰值，单位能耗存在谷值，能达到较为理想的粉磨效果。

Abstract: With the new trend of large-scale, high-efficiency, and energy-saving grinding equipment, using numerical simulation software to simulate and analyze the working conditions of the mill has be-come a commonly used method to improve design efficiency, reduce design costs, and design cycles. This article is based on the discrete element software EDEM and uses the control variable method to simulate the experimental group for setting the cylinder speed, minimum material layer thickness, and feeding rate of the φ2600 Horomill. The grinding characteristics of the mill were analyzed from the perspectives of crushing rate and energy consumption, providing reference for the design and operation parameter selection of the mill. The results show that the higher the rotational speed, the higher the crushing rate. When the rotational speed is higher than 42 rpm, the unit energy con-sumption of grinding increases rapidly; The minimum material layer thickness is negatively corre-lated with the crushing rate, and the unit energy consumption decreases first and then increases, with a reasonable range of 18~24 mm; The feeding rate ranges from 22 tph to 37 tph, and there is a peak in crushing rate and a valley in unit energy consumption, which can achieve an ideal grinding effect.

1. 引言

筒辊磨是法国FCB公司与意大利Buzzi水泥公司共同研发的一种节能高效的粉磨设备 [1] ，与立磨、辊压机同属于料层粉磨技术类磨机，其结合了立磨的结构紧凑性、辊压机的高效节能性以及球磨机的可靠性，在矿山、水泥、冶炼等行业具有广泛的应用前景。就水泥行业而言，我国水泥年产量达22~24亿吨 [2] ，而粉磨系统电耗占全部生产用电的60%~70% [3] ，结合我国绿色可持续的发展理念，“提产、节能、降耗”成为粉磨设备设计的新理念 [4] 。

离散单元法是为了研究物料非连续力学问题而提出的，已逐渐成为解决散体物料颗粒破碎问题的一种有效的仿真模拟方法，广泛应用于矿山破碎、粉磨设备的仿真优化 [5] 。颗粒粘结模型BPM (Bonded Praticle Model)通过众多小颗粒粘结组合起来，能够较为贴切地描述岩石材料的力学性质，因而众多学者针对不同矿石类型的多颗粒粘结模型及破碎机破碎过程展开了大量研究。鲁艳鹏 [6] 等标定了煤的多颗粒粘结参数，与有限元耦合校核了双齿破碎机滚齿的强度。毕秋实 [7] 等建立了赤铁矿石的多颗粒粘结模型，对旋回破碎机型腔进行了参数优化验证。刘钢湘 [8] 通过矿石的多颗粒粘结模型对鄂式破碎机进行了破碎特性仿真。胡名亮 [9] 等通过建立矿石的多颗粒粘结模型对反击式破碎机进行了参数及结构优化。Liu C [10] 等通过建立非规则石灰石多颗粒粘结模型对立磨的粉磨特性展开研究，分析了立磨的结构、运行参数对粉磨效果的影响。

由于立磨、辊压机对筒辊磨的工业冲击，以及筒辊磨大型化过程中存在着筒体变形量大、磨辊两端振动不同步等问题未取得突破性进展，使得国内对筒辊磨的研究相对较少。刘付志标等基于EDEM-Patran/Nastran耦合对φ300筒辊磨进行了层压力学特性分析，分析了喂料量和粉磨压力两个工艺参数对筒辊磨粉碎系统比能耗、比表面积和粒度分布的影响规律 [11] ，但磨机为规格较小的实验机，参数变化范围较小。李晓旭等使用离散元软件EDEM通过对比单颗粒的应力以及应力浮动大小，模拟研究了筒辊磨的筒辊比、喂料量、筒体转速对粉碎效率的影响 [12] 。

本文基于离散元理论建立了多颗粒破碎模型，采用控制变量法对φ2600筒辊磨关键工艺参数筒体转速、最小料层厚度、喂料量进行了对照组仿真分析，从破碎率、单位能耗的角度揭示了关键参数的影响规律，对相关研究进行了补充。

2. 建立模型

2.1. 三维建模

筒辊磨主要由旋转筒体、内衬、耐磨衬板、压辊、滑履等组成，筒辊磨结构示意图如图1所示。利用三维软件Inventor对φ2600筒辊磨主要零部件进行了参数化建模，三维模型如图2所示。

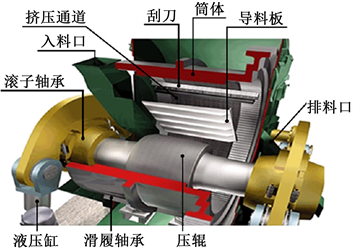
Figure 1. Structural diagram of Horomill

图1. 筒辊磨结构示意图

Figure 2. 3D modeling diagram of Horomill

图2. 筒辊磨三维模型

筒辊磨的工作原理如图3所示，磨机工作时，传动装置带动筒体以超临界速度旋转，物料通过进料口进入筒体，经扬料板进入粉磨区，物料在离心力作用下贴附在耐磨衬板上，运动至刮板装置处被刮刀刮下并在导料板作用下向出料口移动一段距离，落入挤压通道后形成料床；挤压通道由耐磨衬板和压辊组成；耐磨衬板带动物料啮入挤压通道，物料依靠摩擦力带动压辊旋转；在压辊自重及液压系统提供的挤压力作用下，物料被压紧，大颗粒破碎成小颗粒，小颗粒流向颗粒间隙重新排列，料层的密实度增大，颗粒间的挤压力增大，最终颗粒因达到应力极限而破碎成尺寸更小的颗粒排出挤压通道，至此完成一次粉碎；在刮刀、物料推进装置的作用下，物料不断被打散、压紧、破碎，并沿着出料口方向位移，实现可控式循环粉磨，料流轨迹呈螺旋线形式。最后，物料通过出料口的出料罩排出磨外，进入下级系统分选 [13] 。

Figure 3. Schematic diagram of working principle

图3. 工作原理示意图

2.2. 颗粒建模

2.2.1. Hertz-Mindlin with Bonding接触模型

离散元颗粒之间的力学作用是根据Hertz-Mindlin with Bonding接触模型进行的，以EDEM自带的软球模型为基础颗粒模型，两个颗粒之间可发生重叠，能够通过圆柱形粘结键结合在一起，以粘结键代替矿物颗粒中具有凝合力的化学键等作用形式，同时将矿物内部的各部分简化为离散元模型中的球形颗粒，最终形成多颗粒粘结模型 [14] 。颗粒粘结模型如图4所示，合力( ${\stackrel{\to }{F}}_{i,b}$ )、法向扭矩( $M_b^n$ )及剪切扭矩( $M_b^s$ )随着时间步按照公式(1)从零开始增加。

Figure 4. Particle bonding model

图4. 颗粒粘结模型

$\{\begin{array}{c}\Delta {\stackrel{\to }{F}}_b^n=-k_b^n\cdot A_b\cdot v_n\cdot {\Delta }_t\\ \Delta {\stackrel{\to }{F}}_b^s=-k_b^s\cdot A_b\cdot v_t\cdot {\Delta }_t\\ \Delta M_b^n=-k_b^s\cdot J\cdot {\omega }_n\cdot {\Delta }_t\\ \Delta M_b^n=-k_b^n\cdot \frac{J}{2}\cdot {\omega }_t\cdot {\Delta }_t\end{array}$ (1)

其中，

$\{\begin{array}{c}{A}_b=\text{π}\cdot R_b^2\\ J=\frac{1}{2}\text{π}\cdot R_b^4\end{array}$ (2)

式中， $k_b^n$ 、 $k_b^s$ 分别代表法向、切向刚度，v_n、v_t、ω_n、ω_t分别表示法向速度、切向速度、法向角速度和切向角速度。键的横截面积和极惯性矩由A_b、J表示。R_b是粘结键半径，取决于接触的最小球体的直径。

在接触半径内的颗粒通过粘结键相连，当法向力作用大于法向强度或切向力作用大于切向强度时，作用在两个颗粒之间的粘结键断裂，即颗粒发生破碎，如公式(3)所示。

$\{\begin{array}{c}\sigma =\frac{{\stackrel{\to }{F}}_b^{n,total}}{A_b}+\frac{2M_b^n}{J}{R}_b<{\sigma }_c\\ \tau =\frac{{\stackrel{\to }{F}}_b^{s,total}}{A_b}+\frac{2M_b^s}{J}{R}_b<{\tau }_c\end{array}$ (3)

2.2.2. 参数标定

为了更加真实的模拟物料内部之间的凝聚力，需要根据物料的强度特性对物料进行粘结参数标定 [9] 。考虑到筒辊磨的挤压粉磨机理，选择EDEM单轴压缩仿真试验的方法标定物料的粘结参数，单轴压缩试验是获取材料力学参数最直接有效的手段之一。本文选择烧成水泥的原料石灰石为粉磨对象，邢大伟等通过单轴压缩实验等物理实验获取了石灰石的物性参数和接触参数 [15] ，并进行了仿真验证，本文基于其物性参数和接触参数进行EDEM单轴压缩仿真试验以标定与石灰石断裂行为类似的粘结模型参数，其基本物性参数如表1所示，接触参数如表2所示。

Table 1. Physical parameters

表1. 物性参数

Table 2. Interaction parameters of materials

表2. 接触参数

本次标定试验的圆柱形仿真试样与物理试样尺寸一致，高度为70 mm，直径为35 mm，上下承压板以0.1 m/s的速度相向运动 [16] ，时间步为1.097e−6 s，仿真模型如图5所示。根据后处理中的上压板受力及试样的轴向压缩量绘制试样的应力–应变曲线，应力–应变曲线如图6所示，仿真得到的试样极限抗压强度为42.5 MPa，同尺寸下的石灰石极限抗压极限为44.3 MPa，实验与仿真的误差为4.06%，两者的断裂力学特性接近，标定的粘结参数可以用来模拟粉磨石灰石，粘结参数如表3所示。

2.2.3. 建立颗粒粘结模型

本文基于EDEM颗粒替换API插件以及Hertz-Mindlin with Bonding模型建立多颗粒粘结模型，首先利用API将生成的大颗粒从坐标系中移除，再根据组成多颗粒粘结模型的小颗粒的相对位置、数量信息在原大颗粒的位置生成小颗粒以及粘结键 [17] 。

Figure 5. Uniaxial compression model

图5. 单轴压缩模型

Figure 6. Uniaxial compression model

图6. 单轴压缩模型

Table 3. Bonding parameters

表3. 粘结参数

根据理论分析可知筒辊磨的最大入磨粒径一般为压辊半径的0.03倍~0.05倍 [18] ，过大的入磨粒径将导致磨机运行的平稳性变差。本文采用粒颗直径为6 mm球形颗粒通过粘结键与相邻颗粒相连形成粒径为35 mm的多颗粒粘结模型，采用的填充模型如图7所示，小颗粒在模型内部生成后，上、下半球体相向运动至闭合，最终形成规则球形的多颗粒粘结模型，建立的颗粒粘结模型如图8所示，小颗粒数量 [6] 通过以下公式(4)计算得到：

$\xi V_{\text{Real}}=N_{\text{F}}{V}_{\text{Fraction}}$ (4)

其中， $\xi$ 为为体积系数，一般取为0.56；V_Real、V_Fraction分别为大颗粒、小颗粒的体积；N_F为填充大颗粒所需要的小颗粒数目。

Figure 7. Fill model

图7. 填充模型

Figure 8. Multi particle bonding model

图8. 多颗粒粘结模型

3. 离散元仿真

EDEM仿真占用的计算资源与颗粒数量直接相关，考虑到筒辊磨粉磨物料的过程是循环多次的，因而截取喂料粉磨一次的筒体长度进行仿真，且排除衬板形状、压辊安装角等因素的影响，设置筒体、压辊的轴向长度都略大于计算域的长度，同时设置计算域两端为周期边界，粉磨仿真的时间设定为颗粒从颗粒工厂落入挤压通道的时间，以此保证模型的拟实性，离散元仿真模型如图9所示。

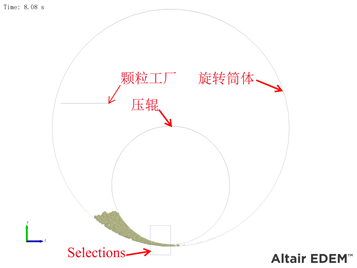
Figure 9. Discrete element simulation model

图9. 离散元仿真模型

大颗粒通过颗粒工厂生成落入挤压通道后，颗粒替换API将其替换成多颗粒粘结模型，随后筒体、压辊以相同的线速度开始旋转，颗粒开始被粉磨，仿真时间步设定为3%瑞利时间，对筒体转速、最小料层厚度及喂料量分别设定单一变量仿真组，每个变量值进行3次仿真并取平均值。

粉磨机械工作的基本技术经济指标是单位电耗(即粉磨单位质量物料的能量消耗)和破碎比(粉碎前后粒径比)。本文以颗粒碰撞总能耗与断裂粘结键数的比值(单位能耗)、断裂粘结键数与总粘结键数的比值(破碎率)来衡量筒辊磨的粉磨特性。在后处理模块，经数学模型分析可知粒径为35 mm的颗粒临界啮入挤压通道的压力角为18˚，以此设定自定义数据处理区Selections的位置和大小，最后通过设置Grid Bin Group的方法来统计粉磨区内的能耗及破碎数据。

3.1. 转速对粉磨效果的影响

筒辊磨以超临界速度旋转，物料紧贴在衬板上形成运动受限的料层。理论上，筒体旋转速度越快，物料通过量越高，破碎效率越高。但是高转速也会导致能耗过高、冲击磨损等问题。因此有必要从颗粒破碎的角度，分析转速对筒辊磨粉磨特性的影响规律。

转速的变化范围设定在1.1倍~2.3倍临界转速之间，不同转速下的破碎率及单位能耗曲线如图10所示，随着转速的提高，破碎率、单位能耗随之升高，破碎率与转速近似呈线性关系。单位能耗曲线在42 rpm (1.6倍临界转速)之前增长缓慢，但在42 rpm之后的增长幅度明显上升，说明超过在某一临界转速，破碎能耗迅速增加，因而转速的选择主要受限于粉磨所需要的能耗。

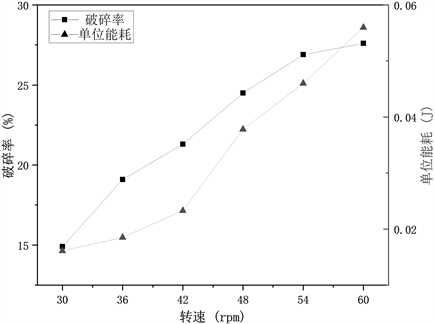
Figure 10. Crushing rate and energy consumption curve at different rotational speeds

图10. 不同转速下的破碎率及能耗曲线

3.2. 最小料层厚度对粉磨效果的影响

衬板内圆柱面与压辊外圆柱面形成了粉磨物料的挤压通道，随着通道收缩，料层厚度越小，在衬板与压辊内外圆柱面最小间隙处存在一个最小料层厚度，一般为压辊半径的0.02倍~0.06倍 [11] 。

不同最小料层厚度下的破碎率及单位能耗曲线如图11所示，颗粒破碎率与最小料层厚度呈负相关，过厚的料层在一定程度上提高了孔隙率，在料层厚度方向上有充分可压缩的空间，颗粒受挤压向四周的孔隙移动，在旋转筒体的带动下，部分颗粒受到来自颗粒、压辊、衬板的压力未达到破碎临界值就已被带出粉磨通道从而破碎的概率降低。

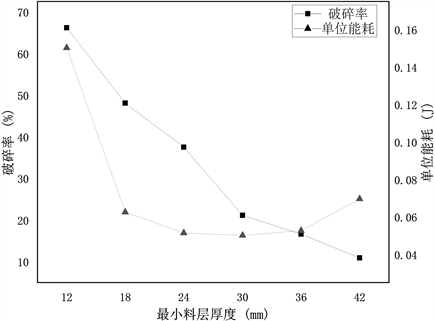
Figure 11. Crushing rate and energy consumption curve for different material layer thicknesses

图11. 不同料层厚度下的破碎率及能耗曲线

观察能耗曲线可知，单位能耗随最小料层厚度先大幅下降后缓慢上升。在最小料层厚度值较小的情况下，单位能耗受料层厚度的影响较大，在最小料层厚度为12 mm的情况下，单位能耗最高为0.11 J，近似于工况为18 mm的3倍。随着最小料层厚度的增加，单位能耗先降后升。

当最小料层厚度过小时，最小料层厚度越小，颗粒的变形量增大，受到来自几何体及周围颗粒的压力越大，当所受压力超过发生破碎的临界压力，则会造成能量损失。从颗粒运动角度来看，最小料层厚度越小，颗粒从刚进入粉磨区至最小料层厚度处的变形量越大，颗粒受力的加载速度增大，要使颗粒发生破碎，快加载施加的力相比慢加载要大，因而提供的破碎总能量溢出，粉磨能耗上升。从孔隙率角度来看，最小料层厚度越小，粉磨区的料层密实度越大，当密实度达到饱和，再降低最小料层厚度也无法提高破碎率，这符合实际生产中挤压“料饼”的情况，施加更多的能量只会造成浪费。

然而最小料层厚度过大时，将导致料层的孔隙率偏大，颗粒间力的传递效率较低，同时压辊、筒体传递的压力在减小，达不到破碎压应力的临界值，所以破碎率降低的同时破碎无用功的比例也相应提高。

综合破碎率和能耗分析，最小料层厚度在18~24 mm范围内的筒辊磨粉磨特性较为理想，保持较低的粉磨能耗的同时破碎率也较高。

3.3. 喂料量对粉磨效果的影响

喂料量较低时，物料没有在磨内形成稳定料层，颗粒间的挤压作用不强，颗粒的破碎量较少，同时单颗粒破碎的能耗也高于料层粉磨，造成了低破碎、高能耗的情况，并且由于没有厚料层的缓冲，磨辊直接冲击衬板，会出现振动较大、耐磨层磨损严重的现象。喂料量过多，大量的物料推挤在挤压通道处，随着筒体转动料层不能顺利通过会出现卡料，料流间断不连续，降低了粉磨效率。

不同喂料量下的破碎率及单位能耗曲线如图12所示，喂料量在15~45 tph范围内，破碎率随着喂料量的增加先升后降，在限定空间大小的挤压通道内，颗粒数越多，料层的孔隙率越低，力在颗粒间传递效率越高，密实的料层限定了颗粒的运动，转动能、能量耗散等形式的能量占比降低，用于粉磨的能量增加，提高了粉磨能量利用率。在45 tph之后的破碎率又出现上升的趋势，原因是粉磨仿真是在静态堆积后进行的，初始孔隙率较高，同时在粉磨区前的挤压区内以冲击碰撞形式破碎的破碎量增加。单位能耗与破碎率呈现出相反的变化趋势，在22~37 tph范围内，料层的破碎率、破碎能利用率较为理想，最佳喂料量取值应在30 tph左右。

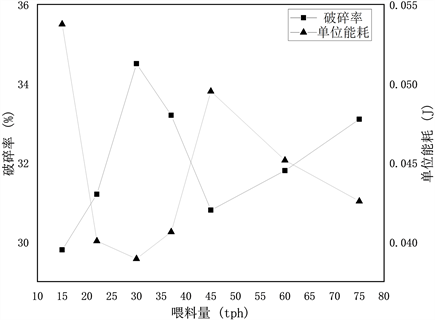
Figure 12. Crushing rate and energy consumption curves for different feed rates

图12. 不同喂料量下的破碎率及能耗曲线

4. 总结

本文基于单轴压缩仿真试验标定了石灰石多颗粒粘结模型的粘结参数，通过颗粒替换API将特定数量的φ6 mm颗粒替换φ35 mm颗粒建立了多颗粒粘结模型，为筒辊磨粉磨仿真提供了条件。根据筒辊磨的粉磨理论对关键参数设置单一变量仿真组，揭示了筒体转速、最小料层厚度及喂料量对颗粒破碎率和单位能耗的影响规律，反映了设备性能，为磨机招标、运行调试提供了技术支持，同时为后续的研究打下了基础。

研究发现：随着转速提高，破碎率、单位能耗逐渐升高，超过一临界值后粉磨能耗急剧上升。最小料层厚度与破碎率呈负相关，单位能耗先降后升，存在能耗“低谷”段。不同喂料量下的破碎率与能耗呈现相反的变化趋势，存在最佳值使得破碎率最高、能耗最低。对于平均入磨粒径在35 mm左右的石灰石生料，φ2600筒辊磨的工作转速不宜超过42 rpm，最小料层厚度取值范围宜为18~24 mm，喂料量取值范围宜为22~37 tph。

参考文献

NOTES

^*通讯作者。