基于梯度的三种优化方法及比较

Three Gradient-Based Optimization Methods and Their Comparison

摘要: 近年来，高速发展的科学技术将人工智能带入大众的视野。机器学习和深度学习作为人工智能的核心技术，引起了众多学者的关注。在机器学习领域，由于目标模型损失函数的复杂性，使得无法快速有效地得到参数估计的表达式，因此，运用基于梯度的优化方法求解该类优化问题很受欢迎，到目前为止最主流的一个算法就是梯度下降法，但在实际应用中，随着数据规模越来越大，传统的梯度下降法训练的过程及其缓慢，已不能够快速有效的解决大规模机器学习问题。所以，在梯度下降方法的基础上进行了改进，提出了随机梯度下降算法。随机方法因其良好的标度特性在大规模应用问题中受到青睐，本文首先详细介绍了梯度下降法、随机梯度下降法及小批量随机梯度下降法三个方法基本思想及其求解最优化问题的具体过程，然后设计数值例子进行模拟实验，并比较三种方法的优劣性，最后通过实验结果得出结论：梯度下降法收敛性较好，但计算效率低，随机梯度下降法计算效率高，而小批量梯度下降法则是介于二者之间。因此在计算大规模的问题时，随机梯度下降法相较于另外两种方法更为有效。

Abstract: In recent years, the rapid development of science and technology has brought artificial intelligence into the public eye. Machine learning and deep learning, as the core technologies of artificial intel-ligence, have attracted considerable attention from numerous scholars. In the field of machine learning, the complexity of the loss function for target models makes it challenging to obtain a rapid and effective expression for parameter estimation. Therefore, the application of gradient-based op-timization methods to solve such optimization problems has become popular. Up to now, the most mainstream algorithm is the gradient descent method. However, in practical applications, as data scales increase, the traditional gradient descent method and its slow training process become inef-ficient in addressing large-scale machine learning problems. Therefore, improvements have been made based on the gradient descent method, leading to the introduction of the stochastic gradient descent algorithm. Stochastic methods, due to their favorable scaling characteristics, have gained popularity in large-scale application problems. This paper first provides a detailed introduction to the basic ideas and specific processes of three methods: gradient descent, stochastic gradient de-scent, and mini-batch stochastic gradient descent, for solving optimization problems. Subsequently, numerical examples are designed for simulation experiments, comparing the strengths and weak-nesses of the three methods. The conclusions drawn from the experimental results are as follows: gradient descent exhibits good convergence but low computational efficiency, stochastic gradient descent has high computational efficiency, and mini-batch gradient descent falls between the two. Therefore, when dealing with large-scale computational problems, stochastic gradient descent is more effective compared to the other two methods.

1. 引言

基于梯度的优化方法，目前国内外已有了较为丰富的研究成果，理论研究也受到了越来越多学者的关注。梯度下降法作为一种反向传播算法最早在上世纪由Rumelhart等人 [1] 提出并被广泛接受，这为后面各种改进算法的出现和21世纪深度学习的大爆发奠定了重要基础。1951年Herbert Robbins和Sutton Monro [2] 首次提出了随机逼近方法，并将其用于一般的回归问题中，1967年Amari S [3] 将其应用到模式识别中，1998年Bottou L [4] 将其应用到神经网络中。在1958年Rosenblatt等人 [5] 将随机梯度下降的思想用于研制的感知机中，1978年Nemirovski和Yudin [6] 叙述了凸凹函数鞍点逼近梯度法。2007年，Shalev-Shawartz等人 [7] 第一次在大规模数据上取得了实质性的成功并提出了投影次梯度算法Pegasos，Arkadi Nemirovski等人 [8] 在2009年比较了随机近似和样本平均近似方法，著名学者Langford [9] 指出，随机梯度下降法在实际使用过程中并不具有稀疏性。2016年Moritz Hardt在 [10] 中将随机梯度下降法用于训练大型深度模型。目前，随机梯度下降法在各领域中得到了广泛应用，在传统的监督机器学习方面，可以应用于求解逻辑回归、支持向量机 [11] 和神经网络 [12] 等，在其他机器学习方面，比如深度神经网络 [13] [14] 、主成分分析 [15] [16] 、奇异值分解 [17] 、典型相关分析 [18] 、手写数字识别 [19] 等应用也是非常成功的。现如今，许多的学者关注到优化算法这个领域，并在传统随机梯度下降算法的基础上进行了深入研究和扩充，不断地形成了各种改进的新算法。这些新算法在不同方面很大程度地提升了算法性能 [20] 。

本文主要介绍梯度下降法、随机梯度下降法和小批量随机梯度下降算法的基本思想和理论框架，并用实际例子来进行数值模拟并进行比较，得出三种方法的特性。

2. 预备知识

我们考虑无约束优化问题

$\min L\left(x\right)$ (2.1)

这里 $x\in R^n$ ， $L\left(x\right)$ 是一光滑的目标函数。

如果有 $x^{*}\in R^n$ 使得

$L\left(x^{*}\right)\le L\left(x\right)$ ， $\forall x\in R^n$

成立，那么我们称 $x^{*}$ 是问题(2.1)的全局最优解。

如果有 $x^{*}\in R^n$ 使得

$L\left(x^{*}\right)\le L\left(x\right)$ ， $\forall x\in N$

成立(这里N是 $x^{*}$ 的一个邻域)，那么我们称 $x^{*}$ 是问题(2.1)的局部最优解。

如果有 $x^{*}\in R^n$ 使得

$L\left(x^{*}\right)<L\left(x\right)$ ， $\forall x\in N$

成立(这里N是 $x^{*}$ 的一个邻域)，那么我们称 $x^{*}$ 是问题(2.1)的严格局部最优解。

定理1：如果问题(2.1)的局部最优解是 $x^{*}$ ， $L\left(x\right)$ 在 $x^{*}$ 的一个开邻域N上是一连续可微函数，那么我们有

$\nabla L\left(x^{*}\right)=0$

定理2： $L\left(x\right)$ 是一凸函数，如果问题(2.1)的局部最优解是 $x^{*}$ ，那么 $x^{*}$ 一定是问题(2.1)的全局最优解。

3. 模型

在机器学习、统计学中，常常需要解决以下类型的无约束优化问题：

$x^{*}=\arg \left(\underset{x\in R^D}{\min }L\left(x\right)=\frac{1}{N}{\displaystyle \underset{n=1}{\overset{N}{\sum }}{L}_n\left(x\right)}\right)$ (3.1)

其中，D，N为已知的正整数， $L\left(x\right)$ ， $L_n\left(x\right)$ 已知， $L\left(x\right)$ 表示N个函数 $L_n\left(x\right):R^D\to R$ 的均值， $L_n\left(x\right)$ 表示N个数据点集合中第n个数据点的损失，x表示参数。

上述类型的优化问题常常应用于神经网络中。而在求解人工神经网络时，可以通过梯度下降算法计算损失函数的值，找出适当的权重与偏置使所求值达到尽可能最小。在实际中，较少使用梯度下降算法，更多的是采用随机梯度下降算法。

4. 方法介绍

(一) 梯度下降法(GD)

梯度下降法(Gradient Descent, GD)在机器学习和深度学习中，广泛应用于求解损失函数或目标函数的最小值。其基本思想是通过迭代不断调整参数的值，以找到能够最小化损失函数的参数值。梯度下降法基于函数的全梯度来进行参数的更新，它告诉我们在当前参数值下，如果增加或减小参数，损失函数会如何变化。梯度下降法的性能和效率受到学习率的选择、初始参数值、损失函数的性质等因素的影响。因此，在实际应用中，需要谨慎选择这些参数以获得最佳的优化结果。

传统的梯度下降法进行梯度更新时使用全梯度，定义如下：

$\nabla L\left(x\right)=\frac{1}{N}{\displaystyle \underset{n=1}{\overset{N}{\sum }}\nabla L_n}\left(x\right)$ (4.1)

算法框架：

梯度下降法在每一次迭代时使用所有样本的梯度来进行参数更新，能够快速准确的确定更新方向，朝着目标所在方向前进，而当样本数目很大时，对所有样本进行梯度计算需要耗费过长时间，训练过程会十分缓慢，所以在大规模机器学习中的适用性相当有限，更适合小规模问题。

(二) 随机梯度下降法(SGD)

随机梯度下降法(Stochastic Gradient Descent, SGD)通常被用于机器学习和深度学习的大规模数据集。它与传统的梯度下降法不同，核心思想是在每次迭代中仅使用一个样本的梯度而不是使用整个数据集的梯度来估计损失函数的梯度，从而使得在迭代中具有更快的收敛速度。这便引入了随机性，因此随机梯度下降法有时会在优化中引入噪声，因此需要仔细选择学习率，以确保稳定的优化结果。

对于随机梯度下降法，不计算完整的梯度 $\nabla L\left(x_k\right)$ ，而是均匀随机的选择一个梯度 $\nabla L_n\left(x_k\right)$ 来代替整体梯度进行梯度的更新，尽管这可能会偏离最小值，但它在预期中是有效的，因为

$E\left[\nabla L_n\left(x_k\right)\right]=\nabla L\left(x_k\right)$ (4.2)

算法框架：

随机梯度下降算法中的每次迭代都与N无关，使用简单、收敛速度快，所以在大规模机器学习算法中非常具有吸引力，得到了普遍的应用，然而，由于每次算法迭代只选择其中一个样本梯度进行参数更新，每次更新后的参数不一定都会按照预期的正确方向移动，这将导致损失函数出现剧烈波动，可能困在局部极小值中。

(三) 小批量随机梯度下降法(MB-SGD)

小批量随机梯度下降法(Mini-Batch Stochastic Gradient Descent, MB-SGD)与传统的梯度下降法和随机梯度下降法都不同，小批量随机梯度下降法的核心思想是在每次迭代中不仅不使用单个样本，也不使用整个数据集，而是使用一个小批量(mini-batch)样本来估计损失函数的梯度，这样既获得了一定的随机性，又提高了计算效率。

对于小批量随机梯度下降法的梯度，我们选取M，一般地， $M\in \left[10,100\right]$ ，此时选择 $\nabla L_{n_1},\nabla L_{n_2},\cdots ,\nabla L_{n_M}$ 来进行梯度的更新，定义如下：

$\nabla L_B\left(x_k\right)=\frac{1}{M}{\displaystyle \underset{m=1}{\overset{M}{\sum }}\nabla L_{n_m}\left(x_k\right)}$ (4.3)

算法框架：

小批量随机梯度下降法利用小批量样本估计梯度，结合随机梯度下降法的收敛性和梯度下降法的稳定性，从而在一定程度上平衡了收敛速度和稳定性，该算法在训练数据集上不断迭代，每次更新朝着预期按照正确的方向进行，在实际应用中，选择合适的小批量大小和学习率很重要，以便获得最佳的优化结果。

5. 算例

例1 求解以下无约束优化问题的最优解：

$\min f\left(x\right)=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left[{\left(1-x_{2i-1}\right)}^2+10{\left(x_{2i}-x_{2i-1}^2\right)}^2\right]}$ (5.1)

图1是当 $x\in R^2$ 时(5.1)的图像，由图可知，该函数没有其他局部极大值和局部极小值，且无论自变量x是趋向于正无穷或负无穷，其函数值都趋向于正无穷，所以该函数有且只有一个全局最小值。

Figure 1. Image when $x\in R^2$

图1. 当 $x\in R^2$ 时的图像

求解无约束最优化问题(5.1)，(5.1)形如(3.1)，我们用本文提到的三者优化方法来进行求解，目标函数的梯度如下：

$\nabla f\left(x\right)=\frac{1}{n}{\left[\frac{\partial f\left(x\right)}{\partial x_1},\frac{\partial f\left(x\right)}{\partial x_2},\cdots ,\frac{\partial f\left(x\right)}{\partial x_n}\right]}^{\text{T}}$ (5.2)

其中，

$\frac{\partial f\left(x\right)}{\partial x_1}=-2\left(1-x_1\right)-40x_1\left(x_2-x_1^2\right)$ (5.3)

$\frac{\partial f\left(x\right)}{\partial x_2}=20\left(x_2-x_1^2\right)$ (5.4)

$\frac{\partial f\left(x\right)}{\partial x_3}=-2\left(1-x_3\right)-40x_3\left(x_4-x_3^2\right)$ (5.5)

$\frac{\partial f\left(x\right)}{\partial x_4}=20\left(x_4-x_3^2\right)$ (5.6)

我们发现，该式子的梯度向量有如下特点，当j为奇数时，形如：

$\frac{\partial f\left(x\right)}{\partial x_j}=-2\left(1-x_j\right)-40x_j\left(x_{j+1}-x_j^2\right)$ (5.7)

当j为偶数时，形如：

$\frac{\partial f\left(x\right)}{\partial x_j}=20\left(x_j-x_{j-1}^2\right)$ (5.8)

求解出目标函数的梯度，用前文所提到的三种基于梯度的方法找出最优解。实验结果如下表1。

Table 1.Experimental results

表1. 实验结果

例2 求解以下Rastrigin函数的最优解：

$\min f\left(x\right)=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left[{\left(x_i-B\right)}^2+10\cos \left(2\pi \left(x_i-B\right)\right)+10\right]}+C$ (5.9)

其中， $B=\arg \left(\min f\left(x\right)\right)$ ， $C=\min f\left(x\right)$ 。

图2是当 $x\in R^1$ ， $B=0$ ， $C=0$ 时(5.9)的图像，从图中可以看出，该函数存在许多非常接近全局最小值的局部极小值。

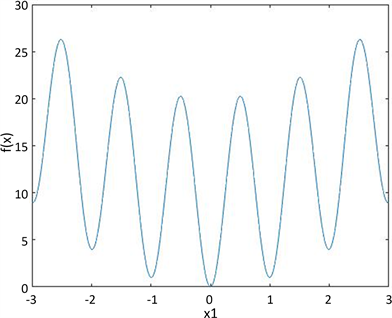
Figure 2. Image when $x\in R^1$ ， $B=0$ ， $C=0$

图2. 当 $x\in R^1$ ， $B=0$ ， $C=0$ 时的图像

由 [21] 可知，随着n取值越大，局部极小值的数量呈指数增长，当 $n=1000$ 时，(5.9)的局部极小值数量达到了5¹⁰⁰⁰。如下表2。

Table 2. The number of local minima changes with the value of n

表2. 局部极小值数量随n取值变化

尝试使用随机梯度下降法求解无约束最优化问题(5.9)，目标函数的梯度如下：

其中，

$\frac{\partial f\left(x\right)}{\partial x_1}=2\left(x_1-B\right)+20\pi \sin \left(2\pi \left(x_1-B\right)\right)$ (5.10)

$\frac{\partial f\left(x\right)}{\partial x_2}=2\left(x_2-B\right)+20\pi \sin \left(2\pi \left(x_2-B\right)\right)$ (5.11)

$⋮$

$\frac{\partial f\left(x\right)}{\partial x_n}=2\left(x_n-B\right)+20\pi \sin \left(2\pi \left(x_n-B\right)\right)$ (5.12)

在我们的数值实验中，假定实验的最终解 ${\bar{x}}_k^{*}$ 与全局最小值 $x^{*}$ 满足：

$\left|{\left({\bar{x}}_k^{*}\right)}_i-{\left(x^{*}\right)}_i\right|<0.25$ ， $\forall i$ (5.13)

则认为实验是成功的，分别对于不同的n进行了100次数值模拟实验，实验结果如下表3。

Table 3. Simulation experiment results

表3. 模拟实验结果

6. 总结与展望

在本文中我们首先简单介绍了在机器学习、统计学中，常常需要解决的无约束优化问题模型，然后介绍了基于梯度的三种优化方法：梯度下降法(GD)、随机梯度下降法(SGD)和小批量随机梯度下降法(Mini-batch SGD)的基本思想及算法步骤，最后在第五章中通过两个数值例子进行实验，并呈现跟我们预想一致的数值结果。通过例子1中实验结果分析得知，当n逐渐增大时，随机梯度下降算法的CPU时间相对于另外两种算法用时明显较短，小批量随机梯度下降算法的误差平均达到了10⁻¹⁰，略优于另外两种算法的平均误差。因此得出结论：梯度下降法在迭代时对所有样本的梯度进行计算，保证迭代时能够朝着极值所在的方向前进，所以当样本数目很大时，训练过程会很慢，此方法在求解小规模问题中是适用的；但在大规模的问题当中这种方法的可行性极低，在这种情况下，随机选择是必要的，并且随机梯度下降算法具有使用简单、收敛速度快的优势，所以较为普遍的应用于机器学习算法中，但是该算法每次参数更新只依赖于一个样本，因此更新方向可能存在较大的随机性，每次更新可能并不会按照正确的方向进行，没有拥有较高的精度，不过幸运的是，在大多数机器学习中是不要求这么高精度的；小批量随机梯度下降法结合了以上两种方法的优点，既可以在较快时间内获得解，又可以获得较高精度的解。最后，例子2中的实验结果表示随机梯度下降法能保证目标函数为凸函数时收敛到全局最优解，若局部极小值很多且与全局最小值非常接近时，则可能仅收敛到局部最优解。

接下来的工作我们会继续对随机梯度下降方法进行相关方面的研究，是否适用于处理一些带有约束的优化问题中，例如将其运用到求解玻色–爱因斯坦凝聚态基态解中。

参考文献