1. 前言
随着城市轨道交通系统的蓬勃发展,地铁交通在人们的日常生活起到了越来越大的作用。不断扩展的地铁网在给人们的生活带来便利的同时,也引发了振动污染问题[1] -[5] ——振动公害,即由交通、生产和建设引发的振动对人们的生活、建筑的安全和精密仪器的正常使用造成的影响,振动公害已成为现代城市建设与发展的关注重心之一。对振动水平进行客观科学的评价,是解决振动公害问题的前提和基础。传统的振动评价方法与其指标是基于受众需求而建立的,如考虑振动对人体舒适度感受的评价标准的振动加速度级(VAL)或振动速度级[6] -[8] 为评价指标,考虑振动对临近建筑物影响时的速度幅值[9] 为评价指标,考虑振动对精密仪器工作性能影响时则多以加速度、速度或位移幅值(峰值) [10] -[12] 为评价指标等等。地铁振动响应作为典型的环境振动信号,其信号特征介于稳态常幅值振动和瞬态冲击振动之间,一方面信号在整体持时过程中峰值包络的起伏不大,峰值或基于全时长的有效幅值评价指标适用;但另一方面,就信号的细节而言,其又是典型的瞬态冲击信号,此时采用峰值、有效值或是以某时间单位计权的振级作为评价均无法对信号的非平稳特性进行较为准确的描述。此外,振动响应的本质是能量的表征方式之一,无论是考虑人体舒适度,还是其对建筑或设备仪器的影响,输入能量的绝对大小是关键因素之一。对于定常幅值振动而言,持时越长,总能量越大,对环境的影响就越大,对于瞬态脉冲振动,峰度系数越大,则意味着能量越大,其影响亦越大。传统的振级或幅值有效值虽是能量的表征指标,但其均是平均能量(功率)的概念,这对于定常稳态振动响应是合理的,即总能量与功率是线性关系;但对于地铁振动响应信号,其整体持时是多个瞬态脉冲信号的序列集合,此时若仍以振级或幅值有效值进行评价,则总能量势必会被低估或高估。本文针对传统振动评价方法对地铁振动信号描述不够全面准确的问题,提出了基于信号时频分析[13] 和时频能量的评价方法,获得对信号时–频域特征及局部化能量、累积能量等指标的完备描述。
2. 信号时频能量分析
本文所采用的时频分布为二次型时频分布,能较好地描述信号的瞬时功率谱密度,是对信号能量的直观描述[13] 。具体的时频分布函数有多种,典型的二次型分布类型包括Cohen类双线性时频分布函数和Affine类双线性时频分布函数,这两类时频分布函数虽时频变换的数学表达式形式不同,但本质上都是对信号时频能量的表达。作为Rihaczek时频分布的实部的改进谱型,Margenau-Hill-Spectrogram时频分布较其他分布类型对能量等效处理的方式不同,其定义的本身即是对离散信号有限能量的直接表达,同时对交叉项、负能量消除、边缘效应优化问题等方面均具有明显优势[14] ,本文对信号时频能量的分析即是基于Margenau-Hill-Spectrogram时频分布进行的。
2.1. Margenau-Hill时频分布
Margenau-Hill类型的时频分布主要分为有两种基本形式,即基本型和谱图型,分别为Margenau-Hill时频分布和Margenau-Hill-Spectrogram时频分布[13] [14] ,其定义[15] 分别如下:
2.1.1. Margenau-Hill时频分布
Margenau-Hill时频分布的定义如下:
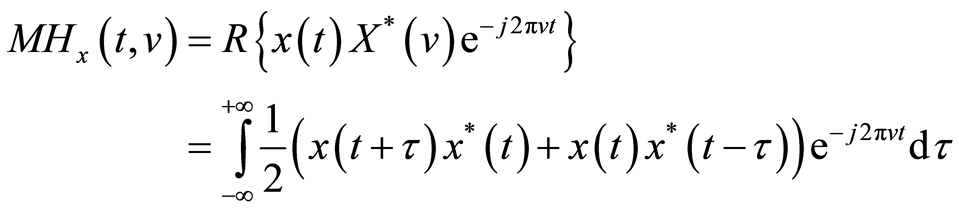 (1)
(1)
式中,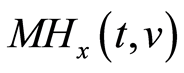 为时频分布系数,
为时频分布系数,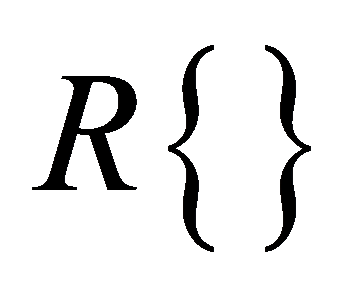 为取实部操作,
为取实部操作, 为虚数单位,
为虚数单位,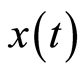 为目标信号,
为目标信号,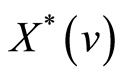 为信号
为信号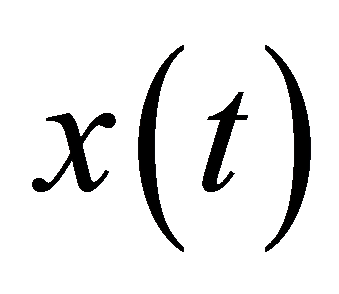 的傅里叶变换的共轭,
的傅里叶变换的共轭,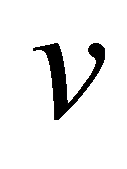 为信号频率,
为信号频率,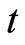 和
和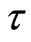 为时间积分变量。Margenau-Hill时频分布用于计算离散信号的Margenau-Hill时频分布系数,亦可计算两个信号的互Margenau-Hill时频分布系数。
为时间积分变量。Margenau-Hill时频分布用于计算离散信号的Margenau-Hill时频分布系数,亦可计算两个信号的互Margenau-Hill时频分布系数。
2.1.2. Margenau-Hill-Spectrogram时频分布
Margenau-Hill-Spectrogram时频分布的定义如下:
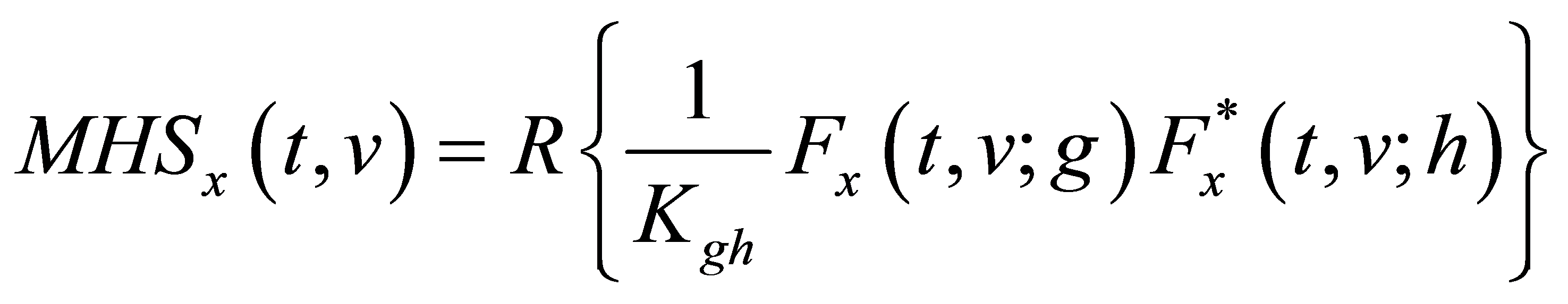 (2)
(2)
式中,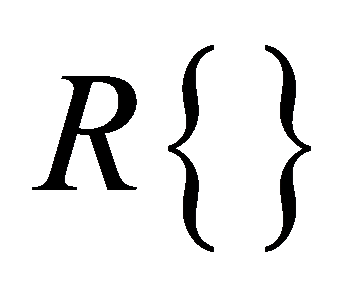 、
、 、
、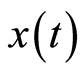 、
、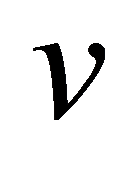 、
、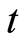 意义同上;
意义同上;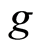 和
和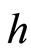 分别为对信号多加的时间窗和频率窗,
分别为对信号多加的时间窗和频率窗,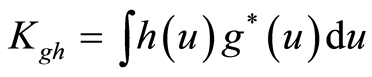 为窗函数的积分,用于调整因信号加窗引入的附加能量项;
为窗函数的积分,用于调整因信号加窗引入的附加能量项;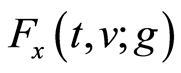 是信号加时间窗的Rihaczek分布,
是信号加时间窗的Rihaczek分布,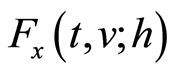 是信号加频率窗的Rihaczek分布。Margenau-Hill-Spectrogram时频分布用于计算离散信号的Margenau-Hill-Spectrogram时频分布谱图,亦可计算两个信号的互Margenau-Hill-Spectrogram时频分布谱图。
是信号加频率窗的Rihaczek分布。Margenau-Hill-Spectrogram时频分布用于计算离散信号的Margenau-Hill-Spectrogram时频分布谱图,亦可计算两个信号的互Margenau-Hill-Spectrogram时频分布谱图。
2.2. 信号时频分布优选
满足基本数学条件的时频分布类型多样[13] [14] [16] ,但并非所有类型的分布在应用于某一类信号的时频分析时均可以得到令人满意的物理意义特征,有时甚至会出现与信号实际物理意义相悖的表现。为此,时域联合分辨率、交叉项、负能量、边缘效应等指标常用来评价一个时频分布的优劣。
为此本文选用高斯线性调频信号作为基元构造一条简单的人工合成信号序列,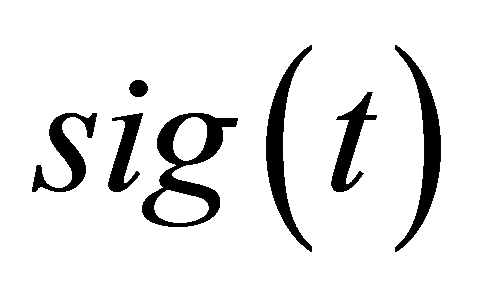 对比地铁引发的场地振动响应实测信号,采用分段衔接的高斯线性调频信号序列,与地铁振动信号的时域特征是相近的。高斯线性调频信号基元的数学表达式为
对比地铁引发的场地振动响应实测信号,采用分段衔接的高斯线性调频信号序列,与地铁振动信号的时域特征是相近的。高斯线性调频信号基元的数学表达式为
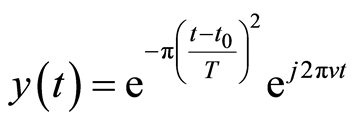 (3)
(3)
式中,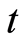 为时间变量;
为时间变量;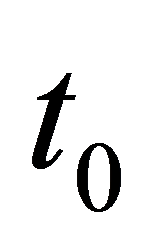 为起始相位时间参考点;
为起始相位时间参考点;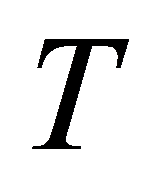 为信号持时;
为信号持时; 为虚数单位;
为虚数单位; 为信号频率。
为信号频率。
人工合成信号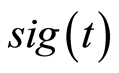 的表达式为:
的表达式为:
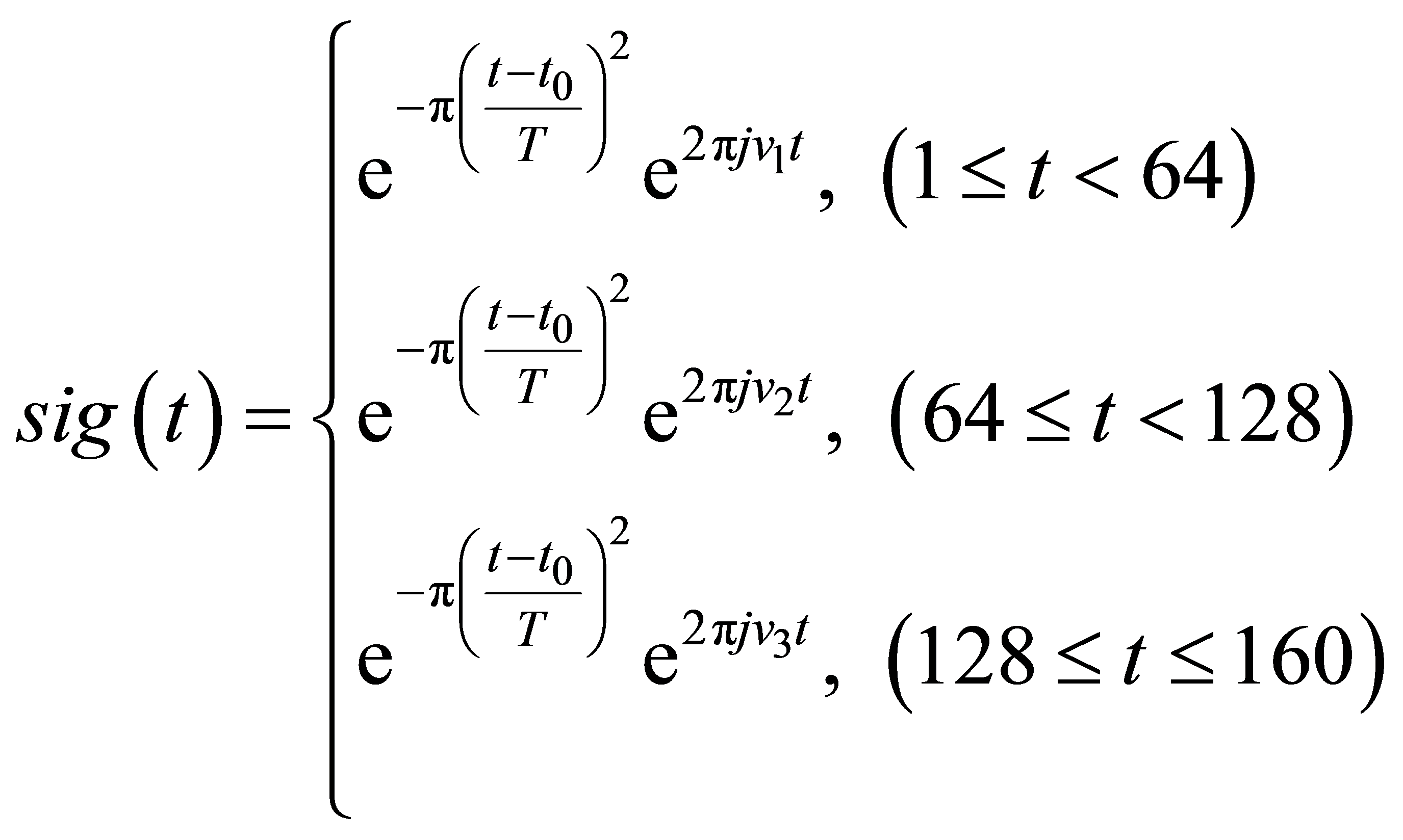 (4)
(4)
本文中,时间采样率取为1,相应的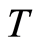 取为16 s,
取为16 s,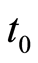 取为32 s,
取为32 s,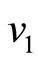 取0.2 Hz,
取0.2 Hz,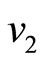 取0.3 Hz,
取0.3 Hz,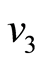 取0.1 Hz,信号时程图如图1(a)所示。
取0.1 Hz,信号时程图如图1(a)所示。
基于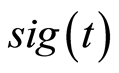 信号,本文采用包括Cohen类和Affine类的共23种二次型时频分布及复Morlet小波分析对信号进行了时频分析,限于篇幅所限,在此仅给出Margenau-Hill-Spectrogram时频分布、MargenauHill时频分布、伪Wigner-Ville时频分布和小波时频分布等分析的对比。如图1可见,在时–频联合分辨率方面,Margenau-Hill-Spectrogram时频分布与伪Wigner-Ville时频分布相近,均优于Margenau-Hill时频分布和小波时频谱,Margenau-Hill-Spectrogram时频分布谱图在获得较好的时域分辨率的同时,其中心频率与信号的真实频率吻合的很好,而小波谱图虽在时域内达到了相近的分辨率,但其频率存在明显的偏峰现象,Margenau-Hill时频分布在时–频分辨率方面表现最差,这主要是由于其引入了较大的交叉项而导致的(如图1(b)中虚线区域即为交叉项);在处理边缘效应方面,Margenau-Hill-Spectrogram时频分布同样表现出其他分布无法比拟的优异性能,Margenau-Hill时频分布、伪Wigner-Ville时频分布在信号末端因振动周期不足引入了明显的边缘项,从而大大降低了这一区域的分辨率。此外,由MargenauHill-Spectrogram时频分布的定义式(式(2))可见,其系数即是信号能量的直接表达(对于任一离散信号,通常将信号各点值的平方和定义为信号能量[14] ),而伪Wigner-Ville时频分布或复Morlet小波系数均是信号能量在某些数学运算条件下的等效或近似表达。基于各类时频分布对多脉冲序列衔接信号的时频分析可知,Margenau-Hill-Spectrogram时频分布对这类信号进行时频分析具有诸多优势,故下文的时频分析均是基于Margenau-Hill-Spectrogram时频分布而进行的。
信号,本文采用包括Cohen类和Affine类的共23种二次型时频分布及复Morlet小波分析对信号进行了时频分析,限于篇幅所限,在此仅给出Margenau-Hill-Spectrogram时频分布、MargenauHill时频分布、伪Wigner-Ville时频分布和小波时频分布等分析的对比。如图1可见,在时–频联合分辨率方面,Margenau-Hill-Spectrogram时频分布与伪Wigner-Ville时频分布相近,均优于Margenau-Hill时频分布和小波时频谱,Margenau-Hill-Spectrogram时频分布谱图在获得较好的时域分辨率的同时,其中心频率与信号的真实频率吻合的很好,而小波谱图虽在时域内达到了相近的分辨率,但其频率存在明显的偏峰现象,Margenau-Hill时频分布在时–频分辨率方面表现最差,这主要是由于其引入了较大的交叉项而导致的(如图1(b)中虚线区域即为交叉项);在处理边缘效应方面,Margenau-Hill-Spectrogram时频分布同样表现出其他分布无法比拟的优异性能,Margenau-Hill时频分布、伪Wigner-Ville时频分布在信号末端因振动周期不足引入了明显的边缘项,从而大大降低了这一区域的分辨率。此外,由MargenauHill-Spectrogram时频分布的定义式(式(2))可见,其系数即是信号能量的直接表达(对于任一离散信号,通常将信号各点值的平方和定义为信号能量[14] ),而伪Wigner-Ville时频分布或复Morlet小波系数均是信号能量在某些数学运算条件下的等效或近似表达。基于各类时频分布对多脉冲序列衔接信号的时频分析可知,Margenau-Hill-Spectrogram时频分布对这类信号进行时频分析具有诸多优势,故下文的时频分析均是基于Margenau-Hill-Spectrogram时频分布而进行的。
3. 地铁信号的时频特征分析
信号时频特性的评价指标主要包括瞬时频率估计、群延迟估计、有效持时、有效频段等特征量[13] 。其中瞬时频率用来表征信号在局部时间点上的瞬态频率特性,整个持时上的瞬时频率反映了信号频率的时变规律;群延迟描述相位变化随着频率变化的快慢程度,直观上就是信号波形包络的时延,单个频率是不存在群延迟,由于群延迟一般适用于强非平稳振动信号的时频特性表征,而本文所关注的地铁引发的场地振动实测响应可被视为弱非平稳信号,故本文对群延迟估计不做讨论;有效持时和有效频段分别用来表征信号主要贡献作用的(比如时频能量等)时段和频段,是分析信号局部化特性的基本量。上述3个特征量的表达式如下:
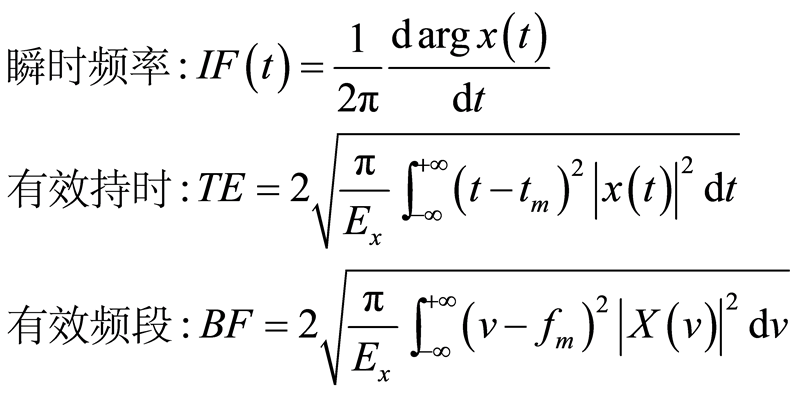 (5)
(5)
式中各字母变量所代表的含义同第2节时频分布定义中各式的字母变量,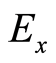 为信号总能量,
为信号总能量,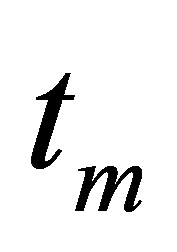 为中心时间,
为中心时间,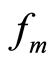 为中心频率。
为中心频率。
本文选取某场地地表某一固定测点的地铁振动响应信号样本共7条[17] -[19] ,信号来源于距离地铁运行中线17 m的测点(详细的测试方案及测试条件等可参见文献[19] ),7条目标样本的加速度时程曲线如图2所示。
我们将整个列车产生的振动信号定义为整体时程信号;将由前后节车厢相连部分的4对轮对产生的振动信号定义为单倍持时信号;将由一节车厢单边的2对轮对产生的振动信号定义为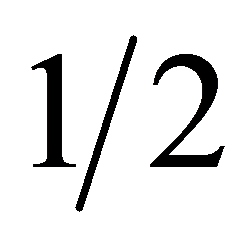 倍持时信号;将由一节车厢单边的1对轮对产生的振动信号定义为
倍持时信号;将由一节车厢单边的1对轮对产生的振动信号定义为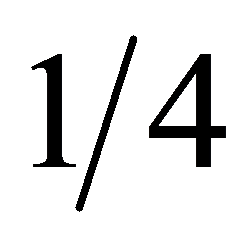 倍持时信号。我们从上述4种振动信号的对比入手,选择比较典型的实测地铁引发的场地振动信号,结合Margenau-Hill-Spectrogram时频分布,对不同持时的地铁引发的场地振动信号的瞬时频率估计(IF)、有效持时(TE)、有效频段(BF)等时频特性进行了分析。计算分析结果如表1所示。
倍持时信号。我们从上述4种振动信号的对比入手,选择比较典型的实测地铁引发的场地振动信号,结合Margenau-Hill-Spectrogram时频分布,对不同持时的地铁引发的场地振动信号的瞬时频率估计(IF)、有效持时(TE)、有效频段(BF)等时频特性进行了分析。计算分析结果如表1所示。
计算结果表明,不同持时的振动信号其振动时频特性有相同点但也存在差别。如图3中所示有效频段、有效持时和中心频率线。观察时频谱图中所框定的信号有效持时和有效频段我们可以看出,在整体时程振动的时频图中,信号的中心频带基本上是稳定在一条直线上(如图中心频率线所标示),随着信号有效持时的减小,出现两个中心频带,说明信号的时频分辨率随着有效持时变短和有效频段变窄在相应提高,在满足不确定性原理的条件下,时频分析可以获得足够高的信号时频分辨率,在表征信号的局部化特征方面具有较好的性能,这说明地铁信号具有较好的局部化时频特征。瞬时频率分析结果说明地铁信
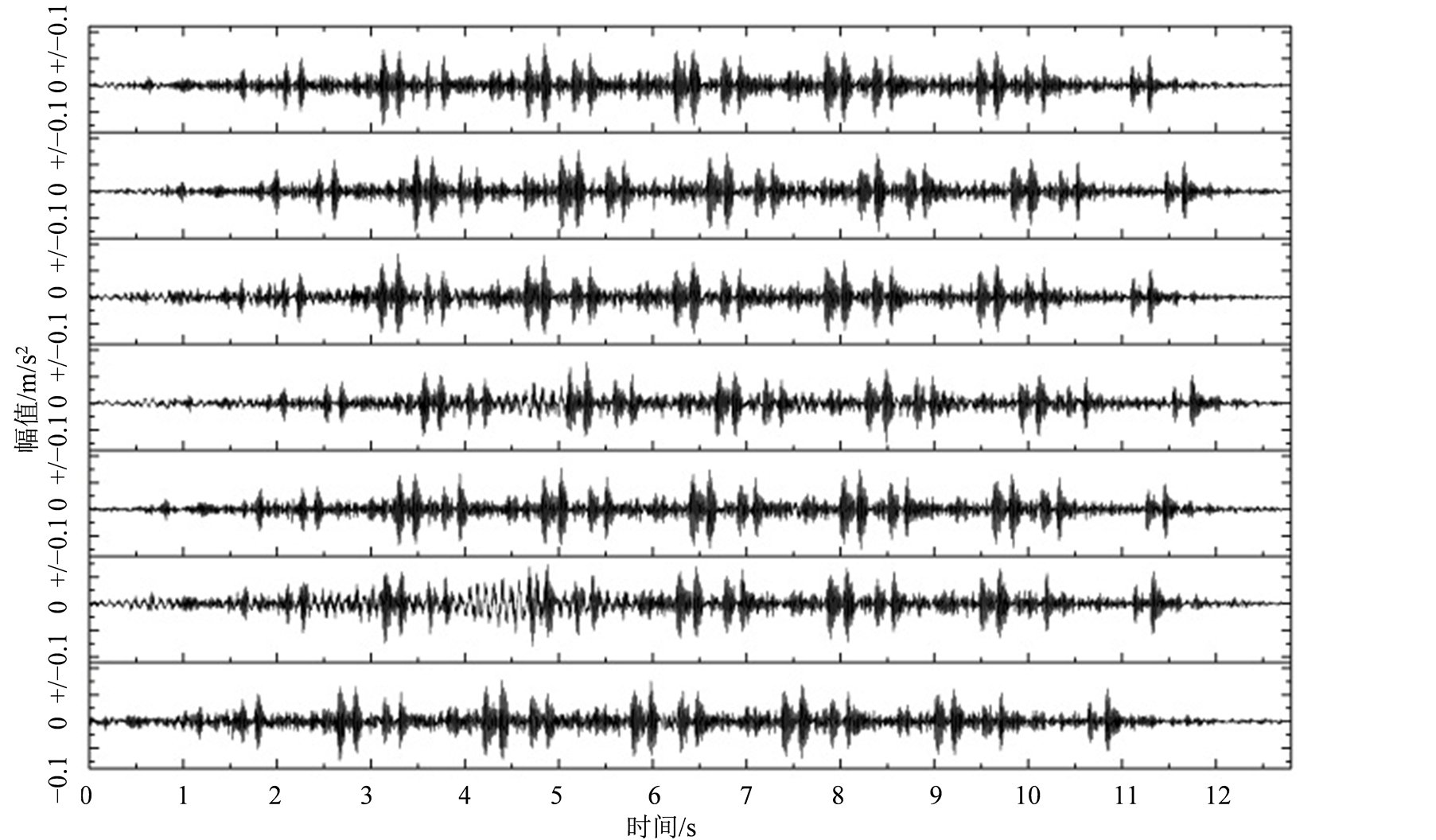
Figure 2. The acceleration time history curve of 7 target signal
图2. 7条目标样本的加速度时程曲线

Table 1. Calculated characteristics of 4 kinds of signals with different time duration
表1. 4种持时振动时程信号的计算特征量
号的振动频率维持在一个稳定的频段内,说明地铁信号的主要频段为55 Hz~64 Hz。综上所述,地铁引发的场地振动信号具有显著的局部化时频特征,采用时频分析方法可以较好的表征地铁信号的时频特征。图3为4种振动时程信号的加速度时程和时频能量谱图。
4. 地铁信号的时频能量分析
4.1. 地铁信号的局部时频能量分析
由第3节的分析可知,地铁引发的场地振动信号具有显著的局部化时频特征,而采用Margenau-HillSpectrogram时频分布能较好的描述其时频特性。考虑到振动响应是能量的表现形式之一,在此进一步定义时频能量指标,以对振动信号的局部化能量和累积能量作深入分析。
振动信号的时频局部化能量E可通过对选定的时频窗内时频分布系数的积分定义如下:
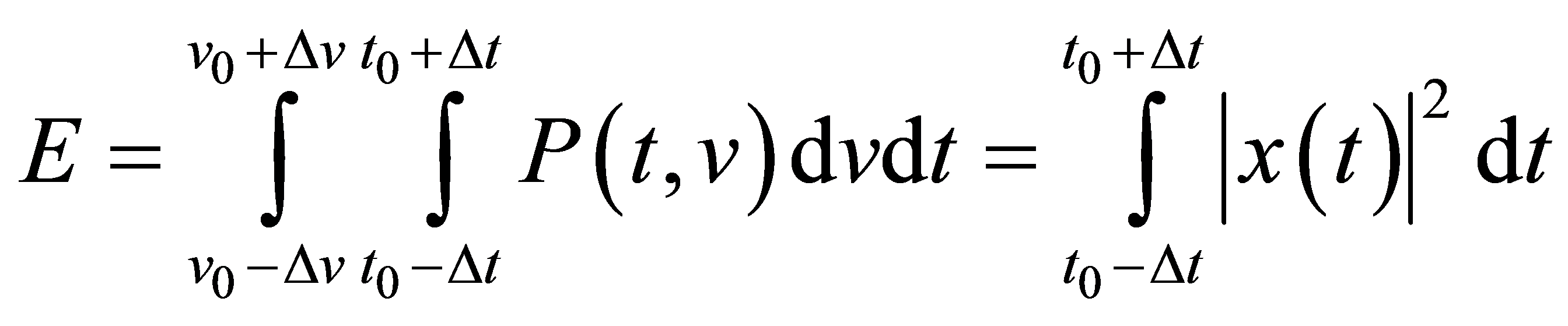 (6)
(6)
式(6)中,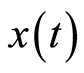 为目标信号,
为目标信号,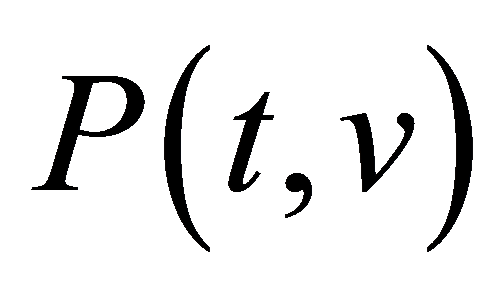 为时频分布系数,
为时频分布系数,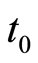 和
和 为分别为信号局部化区域有效持时及有效频段的中心,
为分别为信号局部化区域有效持时及有效频段的中心,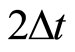 和
和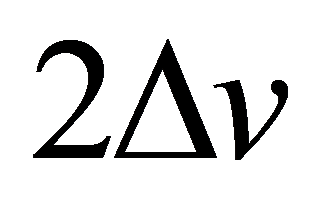 则为有效持时和有效频段,
则为有效持时和有效频段,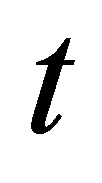 和
和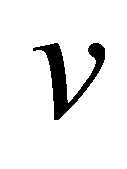 为分别为时间和频率。对于离散信号,则有:
为分别为时间和频率。对于离散信号,则有:
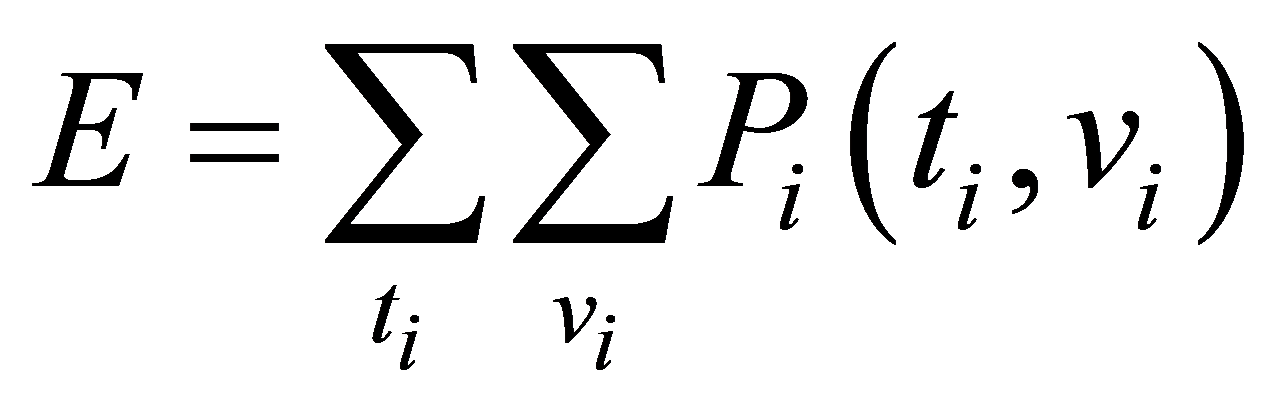 (7)
(7)
选用第3节所示7条信号样本,对样本时程的局部化振动信息进行时频能量分析。由样本时程的时频域特征分析结果可见,对于整列车通行的全部持时过程,可分解为以列车车厢编组方式为基础的车厢轮对造成的多能量振动响应元衔接序列,其基本能量响应元为如图4所示的4次主能量基元和1次次能量基元。本文中将图4中单独一个脉冲定义为能量基本单元,简称能量基元。
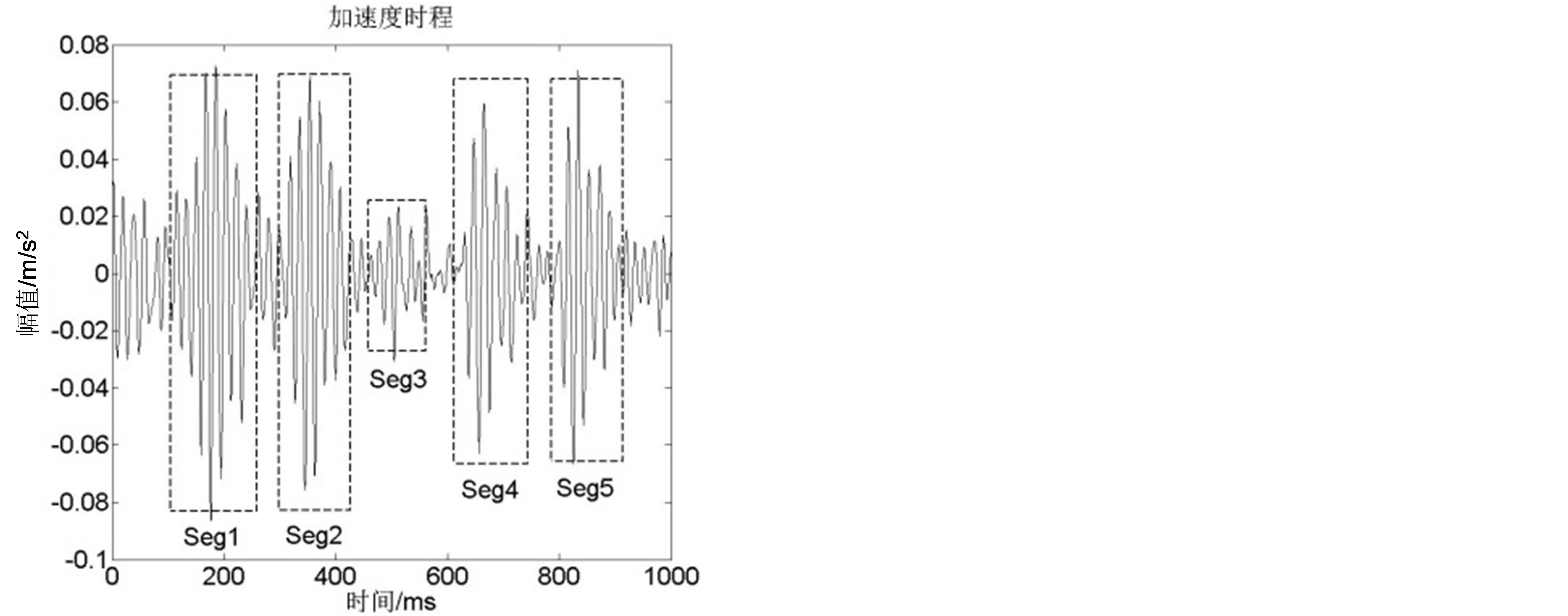
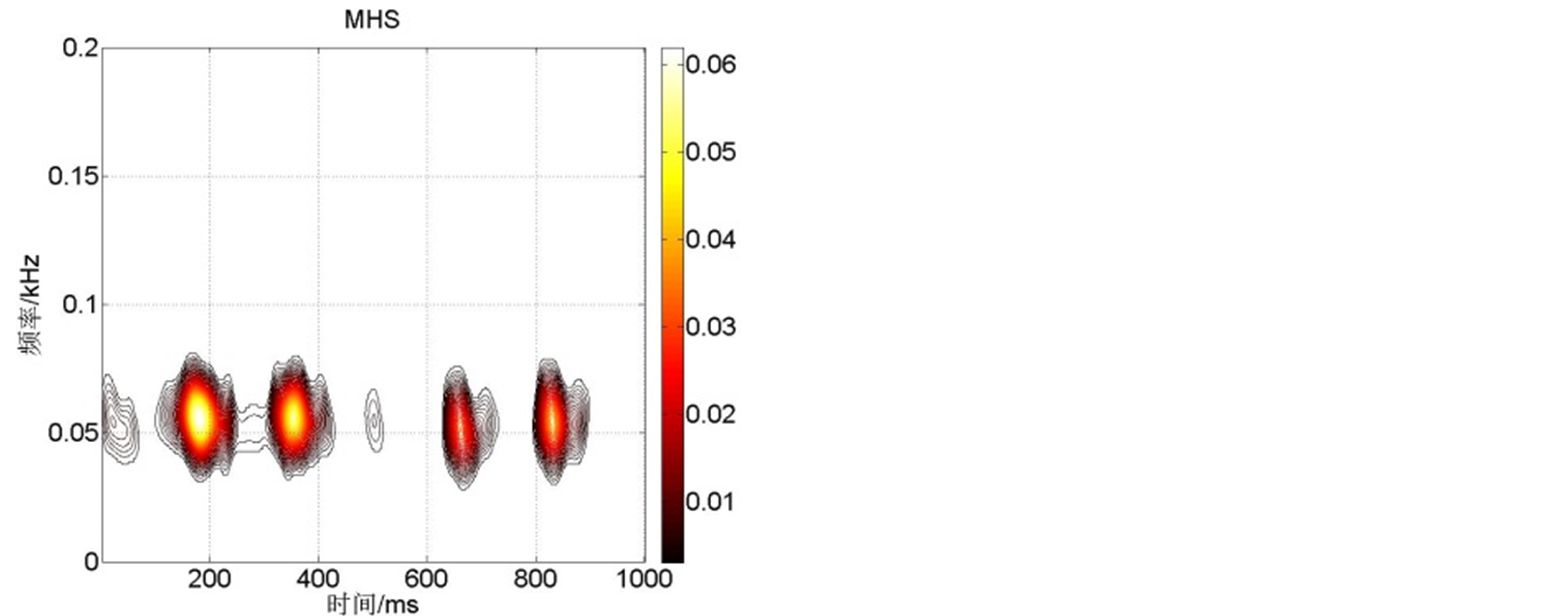
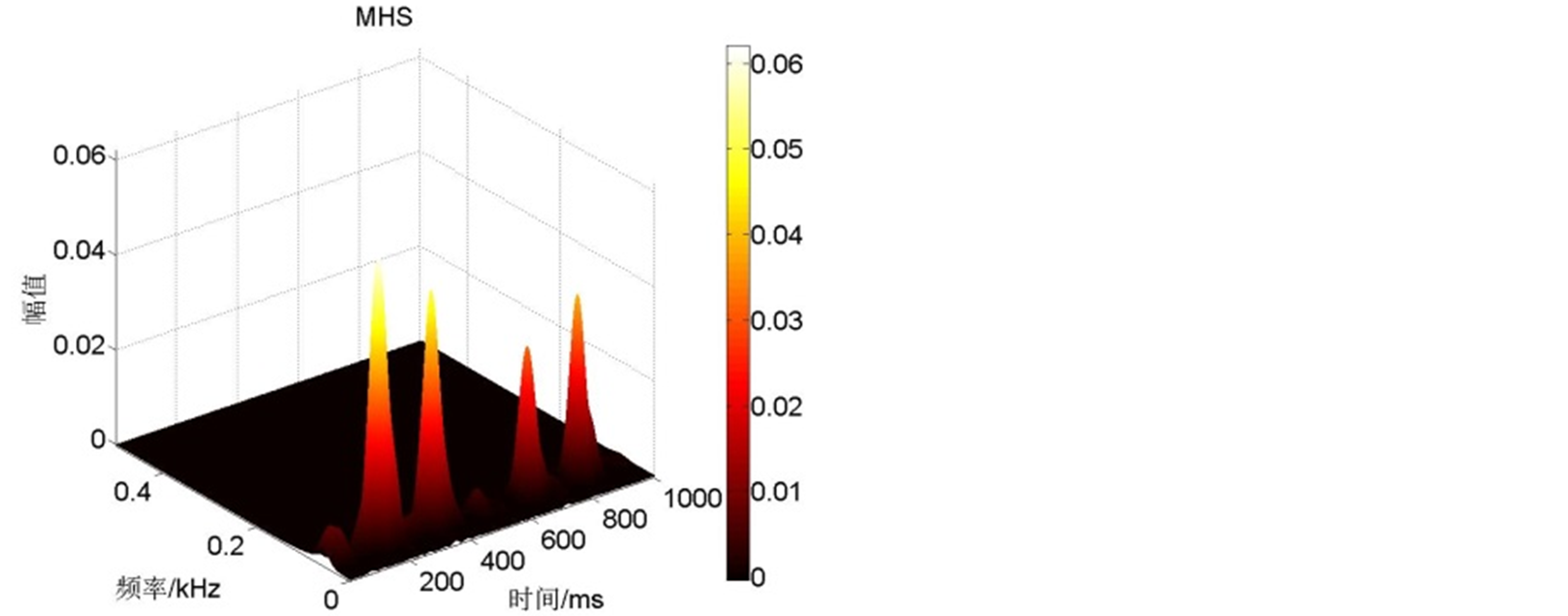
Figure 4. Acceleration time history curve of basic unit time history and the 2D, 3D time-frequency spectrogram
图4. 基本能量响应元加速度时程和2D、3D时频能量谱图
对图4中的基元信号作进一步细节分析,对各组成能量基元Seg1~Seg5分别进行时频能量分析,分析结果见表2所示,由表2可见,能量基元Seg1、Seg2的局部化时频能量接近,Seg4、Seg5比较接近,Seg3与前两类有差别但亦很接近,基于此,可以推断地铁运行引发的场地振动响应的完整持时的累积能量可通过局部化能量的简单数学叠加得到。
对于一条振动时程样本,其局部化能量可分解为3种基本类型,分别对应于Seg1、Seg4和Seg3的局部化能量,由表2给出的相应于7条实测地铁样本信号中Seg1、Seg4和Seg3的局部时频能量统计分析结果可见,对于同一测点地铁振动响应,上述3种基本局部化时频能量的统计结果稳定,变异系数均小于0.23,在获得基本局部化时频能量后,通过局部化能量的简单数学叠加即可得到完整持时的累积能量,基于此,本文进一步对整体持时内的累积能量进行了分析。
4.2. 地铁信号的累积时频能量分析
依然针对上述7个实测样本,沿用第2节对信号持时的定义,统计分析了不同持时的累积时频能量之间的关系,如表3所示,同时,基于表2的3类基本局部化时频能量结果,对信号的累积能量进行线性叠加,结果列于表3第8行,与表3相应的曲线图如图5所示。
各目标样本时频能量累积曲线图如图5所示。
从图5我们可以看出,地铁引发的场地振动时频能量具有明显累积过程,时频能量的统计结果稳定,

Table 2. Time-frequency energy statistics (units: m2/s3); (a) Time-frequency energy statistics of each energy segments; (b) Time-frequency energy statistics of each energy segments from different samples
表2. 时频能量统计(单位:m2/s3);(a) 各组成能量基元Seg1~Seg5时频能量统计;(b) 不同样本能量基元Seg1~Seg5时频能量统计
(a)
(b)
注:表中Avg为平均值;SD为标准差;CV为变异系数(下同)。Avg1、SD1和CV1为对应于每一列数据的计算值;Avg2、SD2和CV2为对应于Seg1和Seg2、Seg3、Seg4和Seg5的计算值。

Table 3. Time-frequency energy statistics of signals with different time duration (units: m2/s3)
表3. 不同持时信号对应的振动时频能量统计(时频能量单位:(m2/s3))
注:表中LS为时频能量基元估算值;Avg、SD和CV均同上。
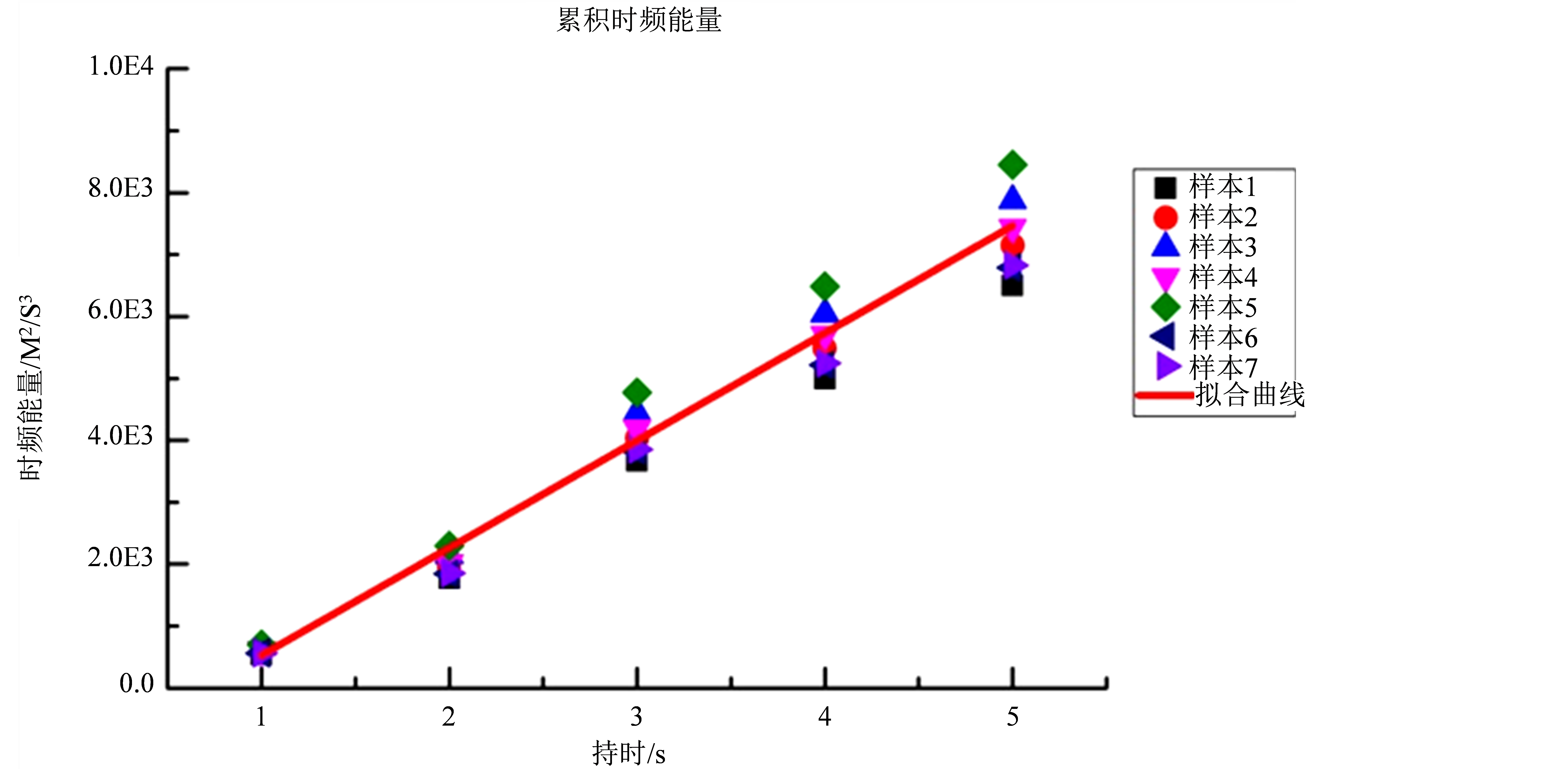
Figure 5. Accumulated time-frequency energy curve of the target signals
图5. 各目标样本信号对应的振动时频能量累积曲线图
同一持时不同样本的时频能量其变异系数均小于0.1;从统计平均值来看,单倍持时信号的时频能量为540.00 (m2/s3),三倍持时信号的时频能量为3494.40 (m2/s3),而五倍持时信号的时频能量为6523.60 (m2/s3),由此可见振动时频能量呈近似线性增加的趋势,拟合线性函数为:
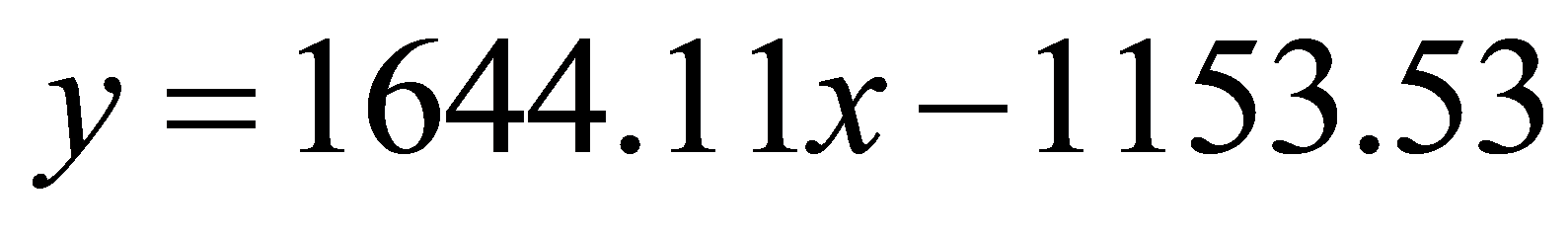 (8)
(8)
式中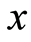 为信号持时倍数。
为信号持时倍数。
进一步我们以同一目标样本,针对不同持时的地铁振动信号的时频能量、振动加速度级和振动幅值做了统计分析对比。以1 s计权值对各统计值进行调幅,不同持时的地铁振动信号的时频能量、振动加速度级和振动幅值的平均化曲线和累积曲线如图6和图7所示。
图7中振级指以1 s为计权得到1~5 s总持时的代表振级(即最大值)计算得到的累积能量;能量指时频累积能量直接计算值;能量元估算值指采用本文定义的能量基元所计算得到的线性叠加值。由式(6)可见,对于1 s的信号能量采用各种方法的计算值应是恒等的,故各点在1 s持时的能量值重合。
从图6我们可以看出,以1 s为计权的平均时频能量、振级和振动幅值在全时长的变化趋势基本一致,时频能量在表征1 s持时信号的能量分布特征与传统方法达到相同的效果。从图7累积曲线图可以看出,采用局部化能量元线性累加的方法得到的总时频能量与直接计算得到的总时频能量偏差很小,可以控制在10%以内,而振动加速度级所得到的计算结果其相对值偏差高于时频能量的计算结果,最大偏差达到了25%,说明传统分析方法在分析地铁引发的场地振动信号时对振动能量存在明显的高估情况。
基于上述推论,我们可以看出振动时频能量兼具振动加速度级或振动幅值等传统环境振动评价方法对信号基本特点的表征作用,同时对信号局部脉冲效应引起的能量局部化特点、累积能量等指标的描述更加准确全面,时频能量适用于地铁引发振动的评价。
5. 结论
1) Margenau-Hill-Spectrogram分布表征多脉冲序列组成的有限持时振动信号时频域特征具有显著优势,同时其是信号能量的直接定义,可以更直观的得到振动信号的时频能量局部化特征及相应的能量表达。
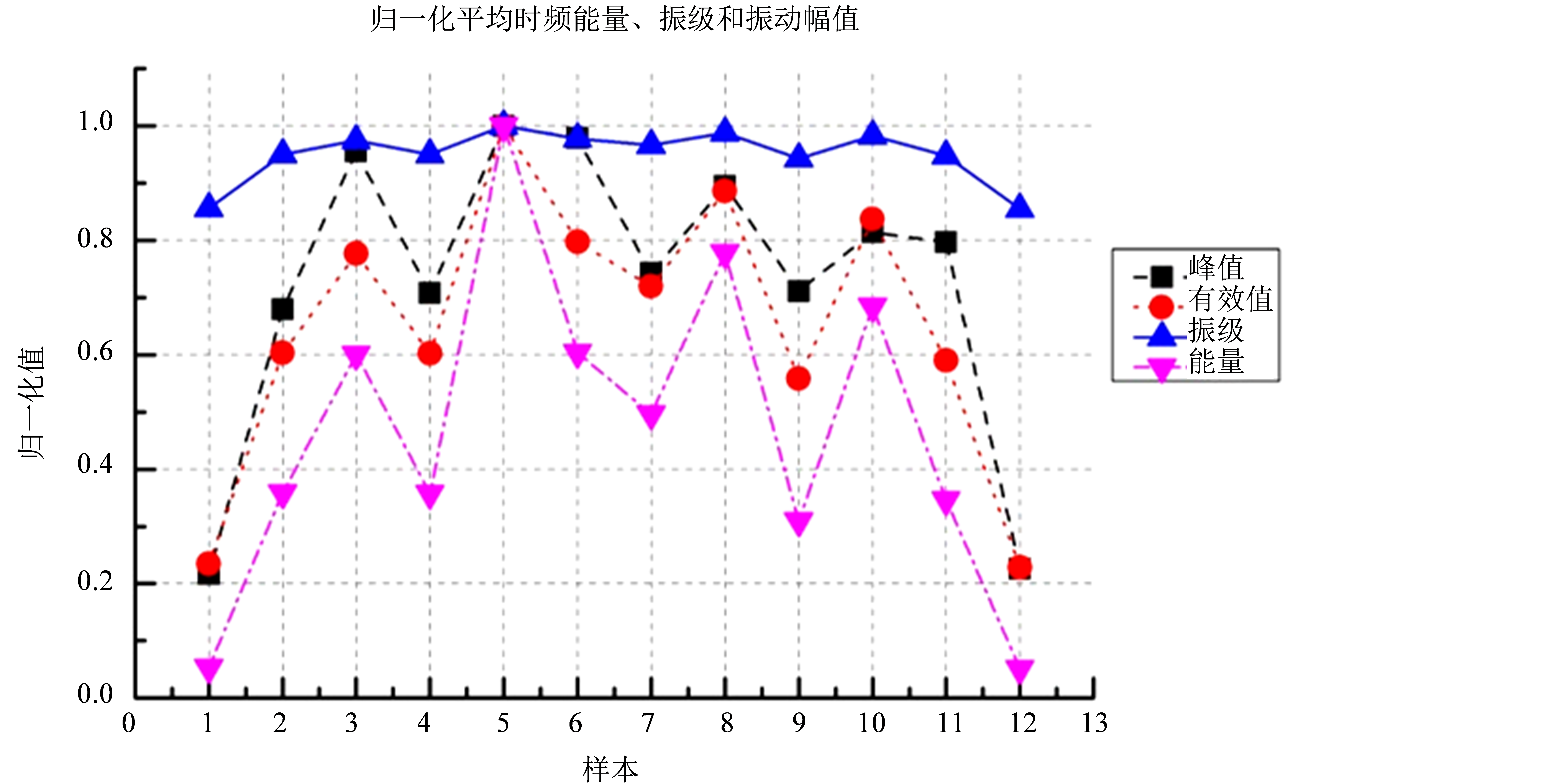
Figure 6. Normalized average time-frequency energy, VAL and vibration amplitudes curve of the target signals
图6. 地铁振动信号1 s时间计权的归一化平均时频能量、振动加速度级和振动幅值曲线图
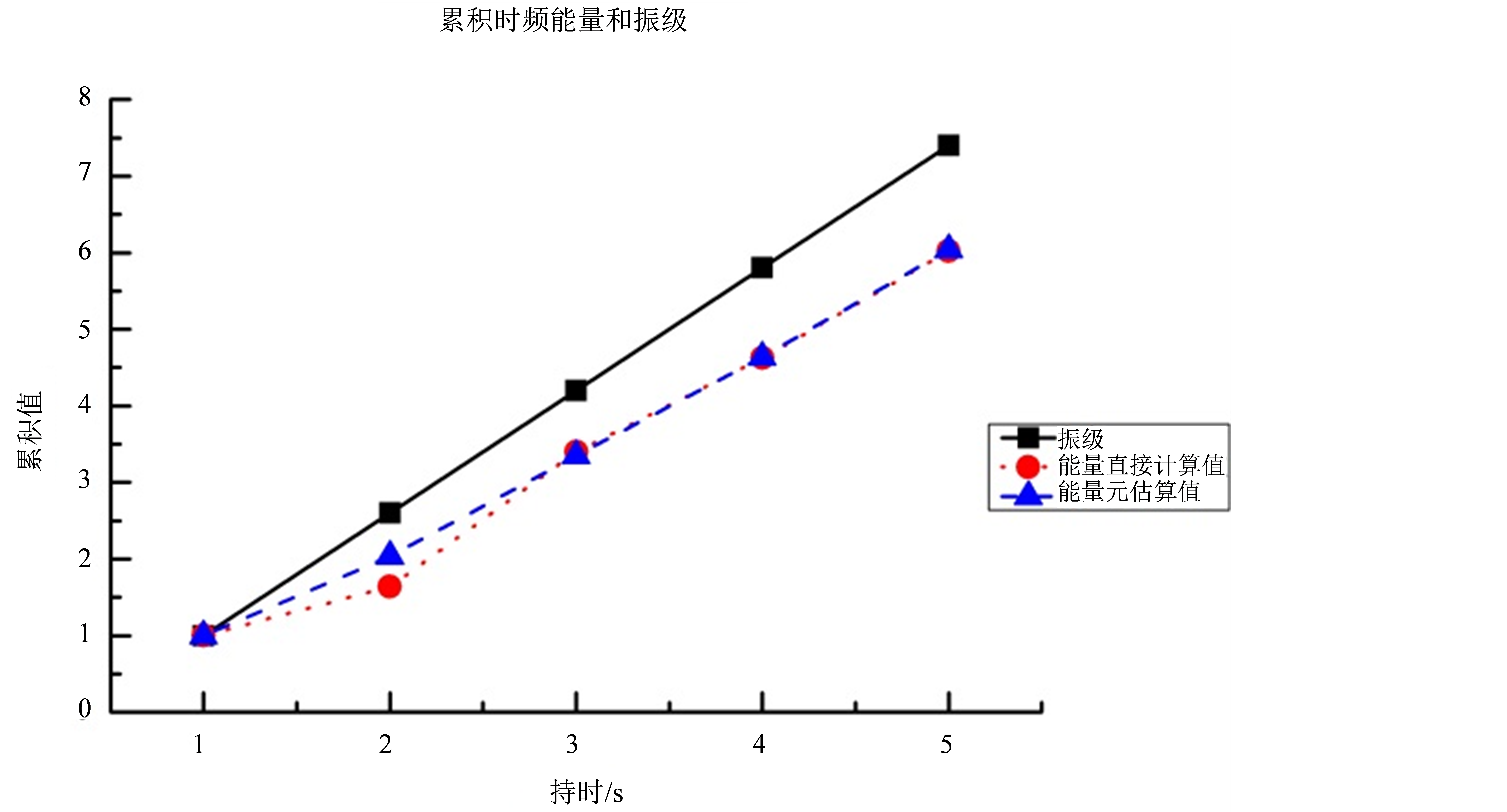
Figure 7. Accumulated time-frequency energy by different calculation methods
图7. 不同计算方法的累积能量比较
2) 地铁引发的场地振动信号在整体持时上表现出较稳定的瞬时频率及有效带宽,但随着对信号细节的深入分析可见,信号的时频局部化特征显著,组成地铁振动信号各信号的局部化时频特征参数特点各异,这些局部化时频特征可应用于振动信号的局部化时频能量分析。
3) 地铁引发的场地振动信号局部化表现为3类基本振动能量基元,分别对应于前一节车厢后轮对、后一节车厢前轮对以及车厢相连处,能量基元可用于近似估算不同持时信号的时频总能量。不同持时的信号累积能量呈现出线性增长趋势,基于3类能量基元的线性叠加估算得到的累积时频能量与信号实际累积时频能量的相对值偏差可以控制在10%以内。
4) 以1 s为时间计权的局部化时频能量对信号能量强度的表征与传统振级分析方法的效果相近,同时又可对信号的局部化特征有更准确的描述,而采用振级或有效值估算信号累积能量,就本文所采用的实测数据分析结果,其偏差最大值则达到25%,而且随着地铁引发场地振动信号持时的不断增加,偏差会越来越大。
地铁引发的场地振动响应信号特征因不同的场地条件、不同的轨道类型、不同的列车及运行状况等各异,本文给出的时频能量分析方法虽是基于某一特定信号而进行的,但其基本过程同样适用于其它地铁振动信号的能量分析。
基金项目
上海市科研计划项目资助,课题编号:13ZR1444800。
致 谢
在此向提供资助的上海市科研计划项目基金表示感谢,向给予转载和引用权的文献所有者表示感谢。

NOTES
*通讯作者。