摘要: 本论文的目的是研究简单线性存在误差项(EV)退化模型的最小二乘估计量中心极限定理的收敛速度。进一步,Miao,Yang和Shen在[1]中对其实际应用做了详细的介绍。
Abstract: In this paper, we study the convergence rate of the central limit theorems for LS estimator in simple linear errors-in-variables (EV) regression model. Further, its application has been introduced detailedly by Miao, Yang and Shen in[1].
1. 介绍
本文我们讨论下面EV模型[2] :
 (1)
(1)
并且满足下列假设:
(1) 是未知常数;
是未知常数;
(2)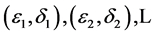 是独立同分布
是独立同分布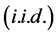 随机变量,
随机变量,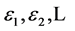 是
是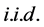 ,
,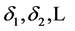 是
是 ,且
,且

(3)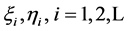 是可观测值。
是可观测值。
根据(1),我们可得出
 (2)
(2)
其中(2)是关于 的常见的退化模型,我们得到
的常见的退化模型,我们得到 和
和 的最小二乘法估计量
的最小二乘法估计量
 (3)
(3)
其中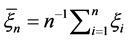 ,我们可用相同的方法去定义
,我们可用相同的方法去定义 。
。
很多学者讨论了估计量的渐近性质和应用。Miao和Liu在[3] 中给出了它的中偏差原理,Miao,Yang和Shen在[1] 中得到其中心极限定理,有如下结论:
定理A:令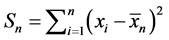 ,假设
,假设
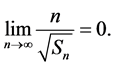 (4)
(4)
并且存在一个常数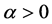 ,使得
,使得 且
且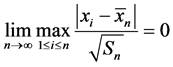 ,
,
则得到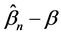 的渐进性质,即
的渐进性质,即
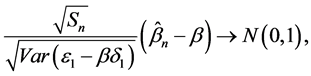
其中 是标准正态分布。
是标准正态分布。
定理B:当满足定理A的所有假设且满足条件: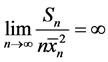 ,则
,则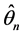 的渐进性质为:
的渐进性质为:

上述结论我们可以参见[4] -[6] ,本文我们讨论定理A和定理B中的收敛速度,也就是中心极限定理的收敛速度。本文中C表示一个正常数。
我们有如下重要的结论:
定理1.1:满足定理A的所有假设,当n充分大时
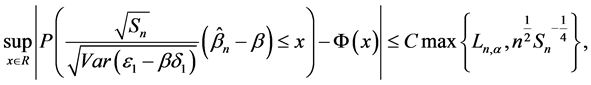 (5)
(5)
其中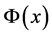 是标准正态分布的分布函数且
是标准正态分布的分布函数且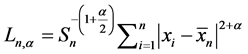 .
.
定理1.2:满足定理B的所有假设,当n充分大时
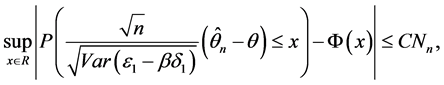 (6)
(6)
其中

注1.1(1)满足定理A的所有假设,我们得到

且 。因此,根据定理1.1有
。因此,根据定理1.1有

(2) 满足定理B的所有假设,我们知道 ,
,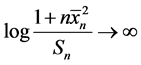 。随即可以得到
。随即可以得到
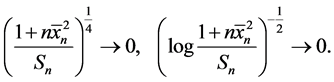
所以有

因此
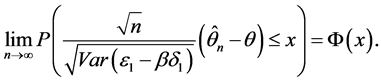
为了证明定理内容,我们给出以下引理。其中(1)的证明方法比较简单,(2)的证明可以参见[7] 。
引理1.1:令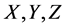 是定义在概率空间
是定义在概率空间 上的三个随机变量,并且
上的三个随机变量,并且 。则对于任意的
。则对于任意的 ,有
,有
(1) 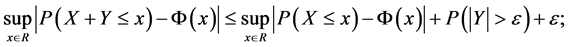
(2) 
2. 定理的证明
下面为了计算方便,我们令
 (7)
(7)
和
 (8)
(8)
为了证明定理内容,我们引入下面引理
引理2.1:对于任意的 ,我们得到
,我们得到

证明:对于所有的 ,根据Holder不等式即可得到
,根据Holder不等式即可得到

所以有
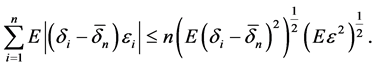
根据马尔可夫不等式可得

引理2.2:对于任意的 ,我们得到
,我们得到

证明:根据简单的计算,我们得到

因此有

最后,根据马尔可夫不等式得到

因为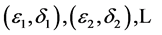 是
是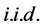 ,根据[8] 中第五章定理6,我们可以得到
,根据[8] 中第五章定理6,我们可以得到
引理2.3:假设存在一个常数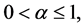 使得
使得 和
和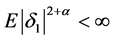 ,则有
,则有

引理2.4:当引理2.3的条件满足时,我们得到
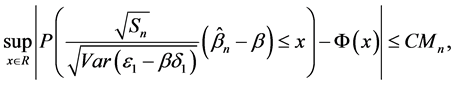
其中

证明:对于任意的 ,根据(7)和引理1.1(2)
,根据(7)和引理1.1(2)
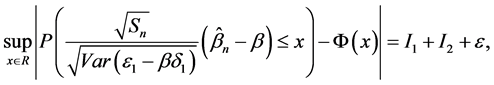 (9)
(9)
其中

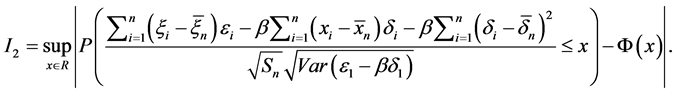
根据引理2.2即可得到
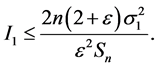 (10)
(10)
现在我们只需去估计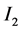 的值。因为
的值。因为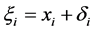 ,所以
,所以 。
。
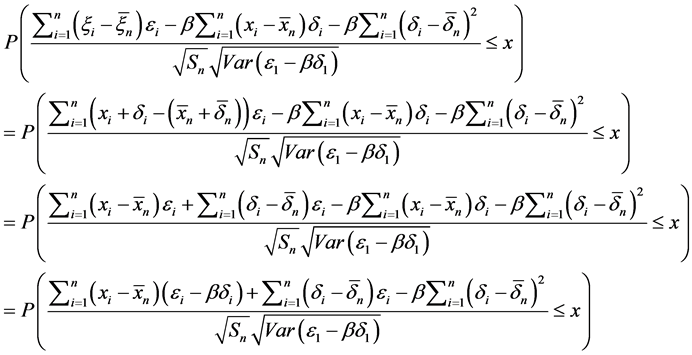
所以根据引理1.1(1),有
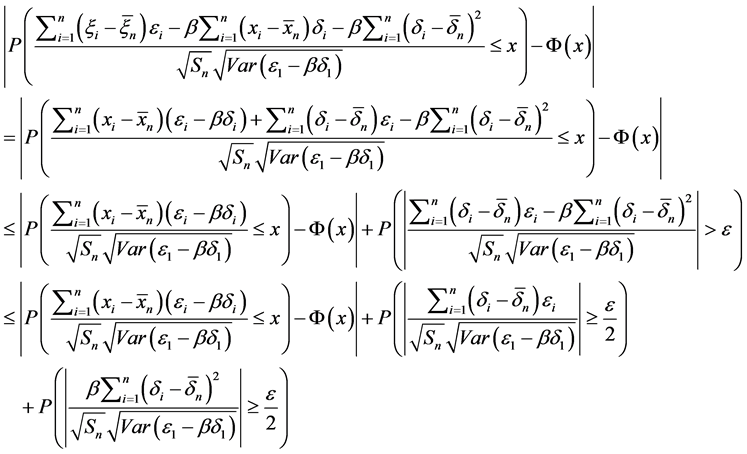
所以
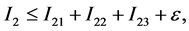 (11)
(11)
其中
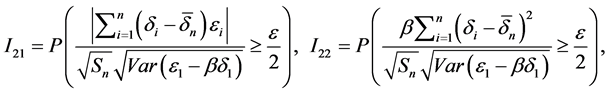

根据引理2.1和引理2.2,我们可以得到
 (12)
(12)
令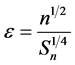 ,结合(9),(10),(11),(12),我们可以得到引理2.4的证明。
,结合(9),(10),(11),(12),我们可以得到引理2.4的证明。
引理2.5:当引理2.3的条件成立时,我们得到

其中
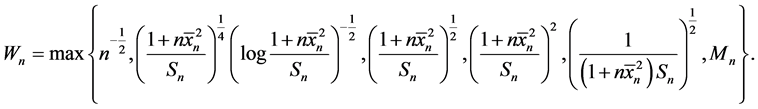
证明:通过(8)和引理1.1(1),对于任意的 ,
,
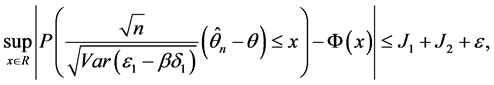 (13)
(13)
其中
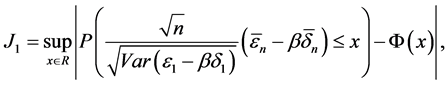
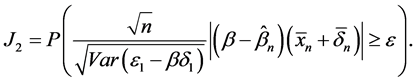
对于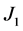 ,根据[8] 中第五章的定理4,我们可以得到
,根据[8] 中第五章的定理4,我们可以得到
 (14)
(14)
下面我们只需去估计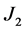 的值。首先我们知道
的值。首先我们知道
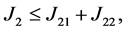 (15)
(15)
其中

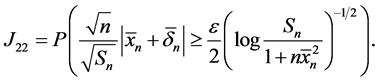
根据不等式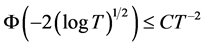 ,其中
,其中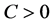 是一个常数。因此根据定理1.1
是一个常数。因此根据定理1.1
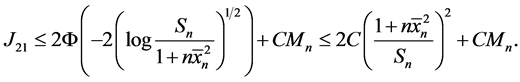
进一步通过Chebyshev不等式,我们有
 (16)
(16)
令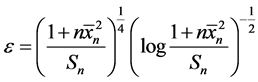 ,结合(13),(14),(15),(16)和
,结合(13),(14),(15),(16)和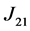 的估计,我们可以证明引理2.5。
的估计,我们可以证明引理2.5。
定理1.1和定理1.2的证明:因为 因此根据引理2.4,当
因此根据引理2.4,当 充分大时,
充分大时,
 (17)
(17)
因此我们可以证明定理1.1。
对于定理1.2,当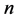 充分大时,
充分大时,

结合引理2.5和(17),我们可以得到定理1.2.
基金项目
本论文是在我的老师和同学于明明的协助下完成的,感谢南京航空航天大学数学系的各位老师给予我的指导和帮助,感谢各位文献作者的成果给予我们的借鉴。