基于坐标修正的定位算法

Geometrical Location Algorithm Based on Position Correction

摘要: 基于接收信号强度值(RSSI)的定位方法以其低功耗，低成本和较低的硬件复杂度等特点被越来越多的应用在室内无线定位中。但RSSI定位也有很多缺陷，如网络稳定性差，受到环境干扰大，从而导致较大的定位误差。对此，提出了一些改进算法。首先连续采集20次RSSI值，采用高斯滤波将干扰较大的样本滤除,然后通过几何算法得到节点坐标。最后提出一种新的修正算法对坐标进行修正。测试结果显示此方法可以将平均误差从2.6 m降低到约1.4 m，修正效果明显。

Abstract: RSSI-based location method is increasingly used in indoor wireless positioning for its low power consumption, low cost and low hardware complexity. However, RSSI-based location also has many flaws, such as poor network stability, large environmental interference, leading to a large position error. For these, the paper puts forward an improved algorithm. First, we collect RSSI value 20 times using a Gaussian filter to filter out error sample and then get node coordinates by geometric algorithm. Finally, a new correction algorithm is proposed to correct coordinates. Test results show that this method can reduce the average error from 2.6 m to about 1.4 m; correction effect is obvious.

1. 引言

随着移动设备，无线网络技术的不断发展，无线传感器网络(wireless sensor networks, WSNs)的应用也越来越广泛。而在无线传感器网络中，位置信息又是至关重要的，事件发生的位置或获取信息的节点位置往往是网络中的重要信息。因此，确定事件发生的位置或者获取信息的节点位置是无线传感器网络最基本的功能之一[1] 。

在室外定位中，全球定位系统(GPS)已经很好的解决了定位问题。它通过GPS接收器接收来自4~20个卫星的信号，然后通过这些信号的到达时间差(TDOA)进行定位。而在室内环境下，GPS系统由于卫星信号受到阻隔而无法完成定位[2] 。因此，通过何种方法进行室内定位并得到较好的效果已经成为无线传感器网络领域的一大研究热门。

在室内定位中，通常的方法是通过测距来实现定位。而测距的主要方法有如下几种：AOA (Angle of Arrival)，TOA (Time of Arrival)，TDOA (Time Difference of Arrival)和RSSI (Received Signal Strength Indication) [3] 。其中RSSI是最常用的测距方法之一。它可以在每次数据传输中获得，不需要额外的带宽和能量，也不需要额外的硬件花费[4] 。然而利用RSSI测距也有着不容忽视的缺点。因为传感器节点往往要部署在复杂的环境中，信号的接收强度会受到多径效应，非视距以及天线增益等影响，对信号的传播损耗产生明显的改变，从而在获取距离信息时产生较大的误差[5] 。因此，要想通过RSSI方法得到较好的定位效果，就必须要尽量的消除RSSI测距过程中的误差。

在RSSI定位过程中，较常用的方法主要有三角质心算法，加权三角质心算法，位置指纹定位算法等。而本文选择一种新的算法，即几何定位算法进行位置确定。几何定位算法就是通过围成正方形的四个锚节点，运用简单的几何知识对盲节点进行定位。然后再提出一种基于几何定位的坐标修正算法，对估计坐标向四个锚节点方向依次进行修正，得到最终结果。

2. 无线信号传播模型及误差分析

2.1. 无线信号传播模型

利用无线信号传输的理论模型，可以通过接收到的信号强度来进行定位。最常用于此方法的传播模型是Shadowing模型[6] 。

Shadowing模型分为两部分，第一部分是pass loss模型，他能够预测出当距离为d时的平均能量。它使用了一个接近中心点的距离d₀作为参考距离，相对于的计算如下：

(1)

其中，是pass loss指数，通常由具体场地测量得到，一般在2~6之间[7] 。

Shadowing模型的第二部分反映了当距离不变时，接收到的能量的变化。它是一个对数正态随机变量，当以dB为单位时，它满足高斯分布。完整的Shadowing模型公式如下：

(2)

为没有任何意义的高斯随机变量。

通常情况下，我们使用公式(2)的另外一种变换公式：

(3)

其中，RSSI为接收到的信号强度(dB×m)，A为一米处的RSSI值，n即前面提到的值，d为测量距离。

2.2. RSSI误差分析

由于RSSI值易受到环境因素的影响，从而产生较大的误差，所以想要得到较稳定的RSSI值就必须先对其进行滤波处理。

图1是发送节点与接收节点间距1 m时，收发300次得到的RSSI值。从图中可以看出由于受到周围物体和人体移动的干扰，RSSI值大体呈现出高斯分布特性。

下面通过两种滤波方法对收集到的RSSI值滤波并进行比较。

首先采用均值滤波方法。均值滤波是指先采集m个数据，然后求其平均值，公式如下

(4)

第二种方法是高斯滤波。高斯滤波器处理数据的原则是对数据进行m次采样，其中必然存在小概率事件。可以通过高斯滤波模型先将这些小概率的数据滤除掉，然后再求平均值。这样就避免了这些概率小，干扰大的数据的影响，从而提高精度[8] 。

对于信号强度而言，假设m次采样符合均值为，方差为的高斯分布，则对于，测量结果x的密度函数为式(5)

(5)

其中，。

选取m = 20，将采集到的300个数据分成15组，然后分别用均值滤波和高斯滤波进行处理。高斯滤波中选取在范围的采样值，然后求平均值。两种滤波结果如图2所示。

从图中可以看到均值滤波虽然起到了一定的滤波作用，但由于其固有的特性，一些扰动大的错误数据并没有被去除掉，而是被平均到各个采样值中，因此最后得到的结果仍然有较大的误差。而高斯滤波采取的是先滤除概率小，干扰大的数据，然后再求平均值，所得到的效果比均值滤波好。因此，本文中选择高斯滤波来对接收到的RSSI值进行处理。

2.3. 参数确定及距离误差分析

要想通过Shadowing模型将测得的RSSI值转换为定位所需的距离值，就必须要确定参数A和n的值。本次试验场地选取在一个10 m ´ 10 m的室内进行，且室内有很多物体，环境比较复杂。选用TI公司的无线收发芯片CC2530作为通信平台。通过一个节点发送数据，另一节点接收数据，在室内不同距

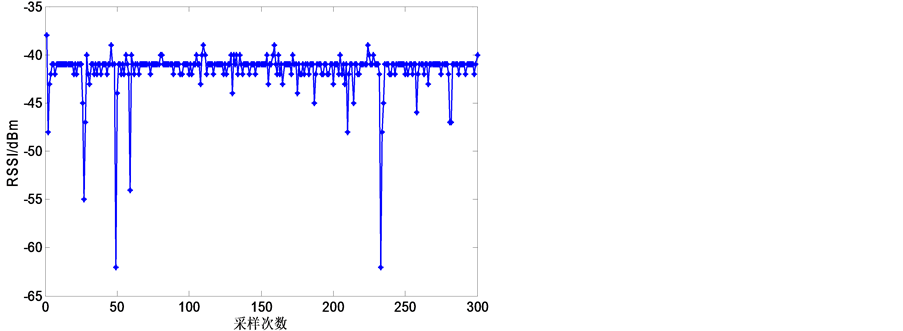
Figure 1. 300 times RSSI value received at 1 m

图1. 1 m处收发300次的RSSI值

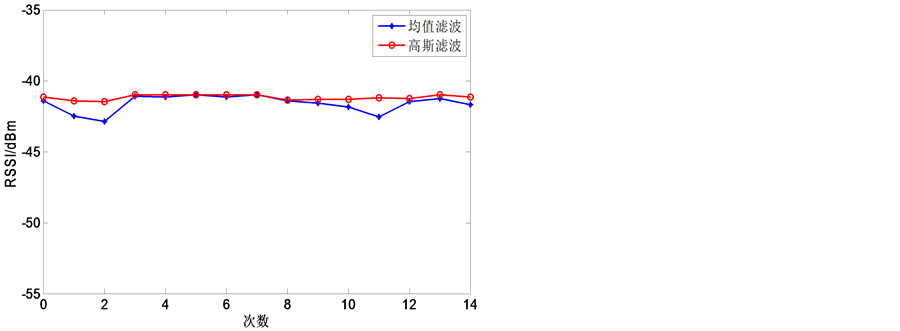
Figure 2. Comparison of mean filter with Gaussian filter

图2. 均值滤波与高斯滤波效果比较

离进行通信，获取对应距离的RSSI值。再利用(3)式确定最佳的A和n。最终确定A = ‒41，n = 3。测量结果和Shadowing模型曲线如图3所示。

由于室内环境等因素的干扰，所测得的RSSI值与距离的关系和模拟的曲线并不完全一致，甚至有些位置会产生较大的误差。距离与误差的关系如图4所示。其中测距误差Er等于实际距离与测量距离之差的绝对值。即

(6)

从图4中可以看出当距离较小时，测距误差较小。但由于实验环境比较复杂，当距离增大时，测距误差明显增大。

3. RSSI定位算法

3.1. 三角质心定位算法

理论上，如果知道盲节点到三个信标节点的物理距离，以三个信标节点为圆心，以相应的与盲节点的距离为半径画圆，三个圆将交于一点，这一点就是盲节点的位置。

但实际情况下，由于环境因素，测量工具等因素带来的影响所产生的测距误差，三个圆不可能交于

一点，而是两两相交。因此，三角质心定位算法就是先将每两个圆的交点计算出来，然后将三个交点所组成的三角形的质心作为盲节点的最终坐标，如图5所示。

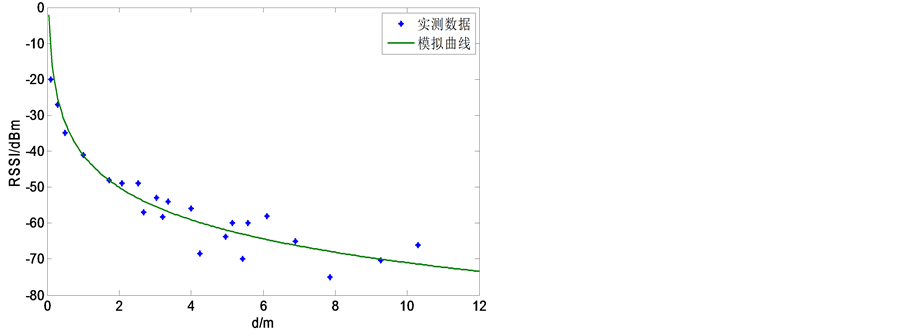
Figure 3. Comparison of measured distance with Shadowing model

图3. Shadowing模型测距与实测结果比较

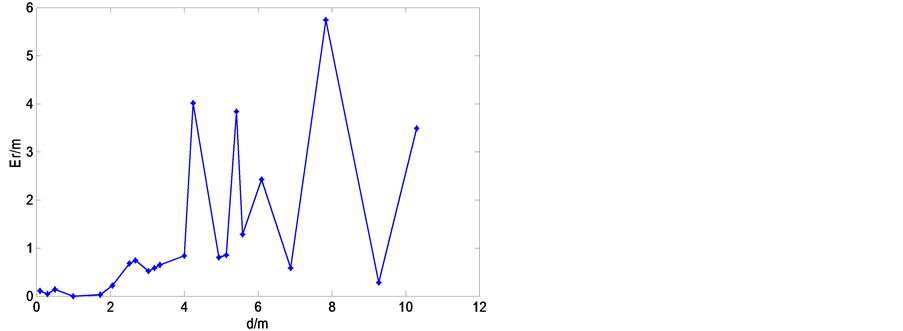
Figure 4. Distance error of Shadowing model

图4. Shadowing模型测距误差

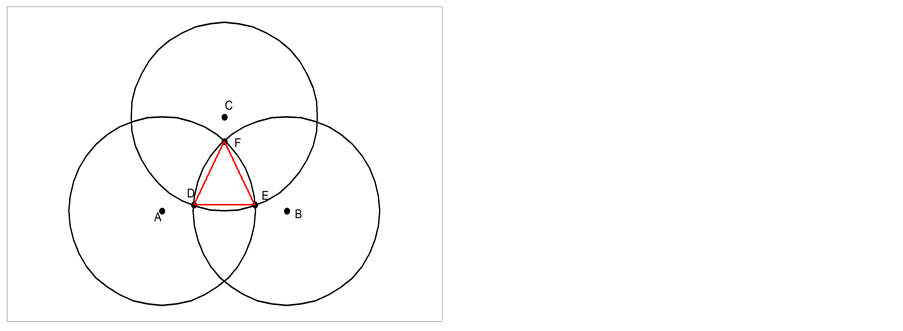
Figure 5. Triangle and centroid algorithm

图5. 三角质心算法

然而使用这一方法的前提是测得的盲节点到三个锚节点的距离均比实际距离大。但通过图3可以看出，使用Shadowing模型测距时，所测得的距离并非总是大于实际距离。这样就容易造成图5中三个圆没有两两相交的情况，从而导致定位失败。

3.2. 几何定位算法

如图6所示，如果在试验场地内用四个节点围成一个边长为D的正方形。以节点1所在位置为坐标原点，节点1与节点2所在直线作为横坐标，节点1与节点4所在直线作为纵坐标，盲节点5到这四个锚节点的距离分别为d₁~d₄，由几何算法可得盲节点的坐标：

(7)

将式(7)中求和平均得到一个稳定性更好的公式[9] ：

(8)

利用公式(8)在试验场地中随机取35处进行定位试验，取D等于4.5 m。图7给出了定位所产生的误差。

由图7可以得出定位平均误差约为2.6 m。误差大多在4 m以下，但也有少数的定位误差较大，达到了6 m以上。由此可以看出，应用几何算法虽然计算简单，定位成功率高，但是当试验环境复杂，测距误差较大时，得到的定位效果并不是很好。这主要是因为几何定位算法仅仅是依靠理论上的几何关系得到的，并没有任何对坐标进行修正的内容。因此当测距值与实际的距离值偏差较大时，定位产生的误差也会较大。下面就提出一种针对几何算法的坐标修正算法。

4. 针对几何算法的坐标修正

首先对几何算法中的公式(7)进行分析。以公式中求x轴坐标的式子为例，将此式分开写得下式：

(9)

(10)

几何算法是通过对公式(9)和(10)求和平均作为最后定位坐标的x轴。然而由于误差的影响，我们对式(9)和(10)分别计算时必定会得到两个不同的值x₁和x₂。当x₁大于x₂时，因为D值不变，则有d₁或d₃的值比实际值偏大，或者d₂或d₄的值比实际值偏小。另外，由图4可以看出，当测量距离变大，测距误差也会变大。因此我们可以认为d₁与d₃中的较大值的测距误差更大。同样，当x₂大于x₁时，有d₂或d₄比实际值偏大，而d₁或d₃比实际值偏小，且d₂与d₄中的较大值的测距误差更大。

根据上述的信息，本文通过公式(11)对定位坐标进行修正。

(11)

其中。表示号锚节点的测量距离，表示用几何算法得到的定位坐标到号锚节点的距离，为修正权值，其中表示比实际值偏大的两个测距值中较大的那个所对应的权值，表示比实际值偏大的两个测距值中较大的那个所对应的权值，表示比实际值偏小的两个测距值所对应的权

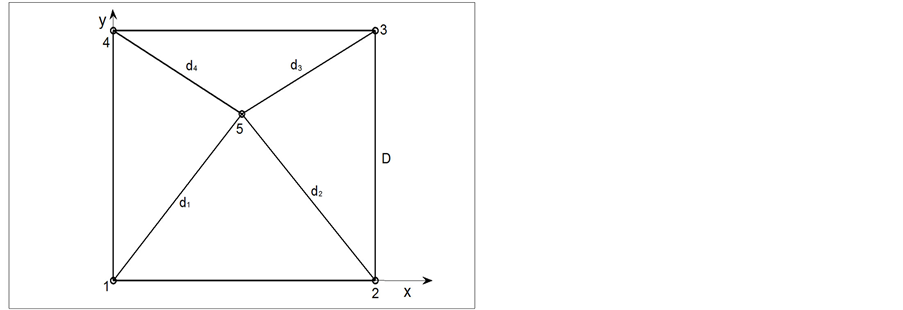
Figure 6. Geometrical location algorithm

图6. 几何定位算法

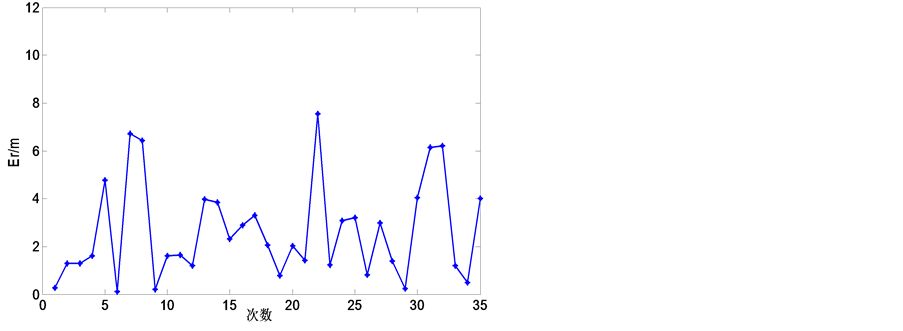
Figure 7. Error by geometrical location algorithm

图7. 利用几何算法定位产生的误差

值。的取值与具体的试验环境有关，本文中选取，，。

下面通过具体例子来描述修正算法。如图8中所示，定位节点的实际坐标为(6.4, 1.6)，四个锚节点所测得的距离分别为d₁ = 7.36 m，d₂ = 2.96 m，d₃ = 2.15 m，d₄ = 11.66 m。通过式(8)计算得到坐标为(12.1, −2.1)，误差为6.8 m。通过公式(9)和(10)得到x₁ = 7.3，x₂ = 16.8。另外，d₄大于d₂。所以可以认为d₂和d₄大于实际值，d₁和d₃小于实际值，且其中d₄的偏差较大。

下面通过公示(11)对坐标进行修正。由于d₄偏差最大，先将坐标向4号锚节点进行修正，修正距离为，权值为，然后再向2号锚节点修正，修正距离为，权值为，最后再向1号和3号锚节点进行修正，修正距离分别为和，权值为。通过这四次修正得到最终的坐标节点为(6.07, 1.9)，误差为0.4 m。

利用此方法对上文35个定位坐标进行修正，并与修正前的误差比较，得图9。从图中可以看出应用修正算法对坐标进行修正之后，所有误差均小于4 m，且多数都在2 m以下，平均误差减小为1.4 m，修正效果明显。

5. 总结

针对无线传感器网络中基于RSSI定位由于环境等因素产生的RSSI值的误差，本文通过先采用高斯滤波算法滤除干扰较大的错误数据，再将数据平均，得到较稳定的RSSI数据。然后运用Shadowing模型

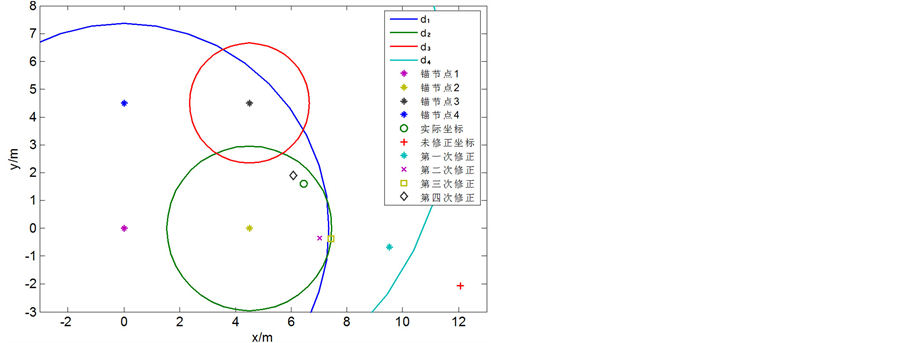
Figure 8. Coordinate correction algorithm examples

图8. 坐标修正算法示例

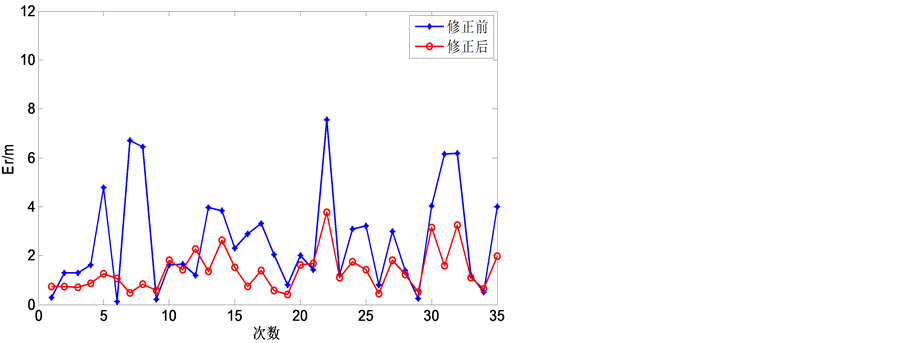
Figure 9. Comparison of positioning errors before and after correction

图9. 修正前后定位误差比较

得到对应的距离。之后采用一种计算简单，定位成功率高的几何定位算法对盲节点进行定位。最后，提出一种坐标修正算法对坐标进行修正，将平均误差从2.6 m减小到1.4 m，效果明显。然而基于RSSI的定位方法由于其独有的特点，想要实现精确，稳定的定位效果仍然非常困难，这也是下一步的研究重点。