基于GA和灰色SVC的图像通用密写分析

Universal Steganalysis for Image Based on Genetic Algorithm and Grey SVC

摘要: 在以支持向量分类机(Support Vector Classifier, SVC)为分类器的图像通用密写分析中，离群样本对最优分类面判别的影响成为导致分析性能不高的原因之一。文中提出一种新的密写分析算法。该算法首先在小波域上提取噪声信号的特征，然后利用遗传算法(Genetic Algorithm, GA)搜索最优类特征，最后将样本特征与最优类特征的灰色关联度参与到SVC的训练中，构造一个灰色支持向量机作为分类器。与采用相同特征的Holotyak算法相比，文中所提的通用密写分析算法的分类结果更好。

Abstract: The isolated samples can produce some affect on distinguishing the best classifying plane, which becomes one of causes of less performance of universal steganalysis that uses Support Vector Classfier (SVC) as classifier. This paper proposes a new universal steganalysis algorithm. The algorithm firstly catches characteristic of noise signal in wavelet domain. Then utilizes Gentic Algorithm (GA) search the best characteristic of species. Finally makes grey relational degree between sample characteristic and the best characteristic of species participate in training of SVC, thus constructs a Grey Support Vector Machines (GSVM) to be a classifier.

1. 引言

密写分析的目的在于揭示媒体中秘密信息的存在性。目前有很多针对特定隐藏方法的密写分析法，然而随着密写的不断发展，方法多样性使得对隐藏信息的检测变得非常困难，其结果是密写分析的发展永远落后于密写。显然，仅持有可能含密的图像、对可能使用的密写算法全然不知的完全盲分析是密写分析的重要研究内容。这种密写分析方法不局限于单一的密写算法，通常对几种密写算法都适用，所以又称通用密写分析。

著名的通用密写分析技术，例如I. Avcibas等 [1] 提出的利用图像最低位平面和次低位平面的多项二值相似性测试作为特征空间，采用SVC分类的算法。Siwei等 [2] 进一步采用QMF分析图像小波系数及其预测误差的高阶统计量，对一类支持向量机进行训练。T. Holotyak等 [3] 提出一种新的在图像小波域上提取噪声成分特征，用两类SVC进行分类的方法。这些技术的相同之处是都用支持向量机作为分类器，但是在支持向量机方法中，确定最优分类超平面的支持向量位于类边缘，而离群样本往往也位于类边缘附近，就这个问题，线性不可支持向量分类机引入松弛变量来容许一定数量的错分类样本的存在，这些错分样本会影响最优分类面的判别，从而影响分类器的性能，成为分析性能不高的原因之一。

文中将提出一种新的以GSVM为分类器的图像通用密写分析方法。首先选取T. Holotyak通用密写分析中的33个噪声高阶统计量作为特征向量，利用遗传算法对训练样本进行搜索，得到最优类特征向量，然后运用灰色关联分析求出不同训练样本的特征向量与最优类特征向量的关联程度，将其参与到支持向量机的训练中，以减小离群样本的分类误差在支持向量机目标函数中的影响，称经过这样训练的支持向量机为GSVM，最后运用训练好的GSVM进行分类检测。

2. 遗传算法和灰色关联分析

最早系统地提出GA的是J. H. Holland [4] . GA将问题的可能解集通过基因编码构成初始种群(父代)开始迭代，计算父代个体的适应度，如果满足优化准则，就跳出迭代；否则，通过选择、交叉或基因重组、变异等操作形成新的个体(子代)，将子代插入到父代中，重新开始循环，直到满足优化准则，使种群进化到包含近似最优解的状态。

找到最优解后，可运用灰色关联分析(Grey Relational Analysis, GRA)计算父代中可能解与其的灰色关联度。灰色关联度的计算描述如下 [5] ：

设参考序列

$x_0=\left(x_0\left(1\right),x_0\left(2\right),\cdots ,x_0\left(n\right)\right)$ (1)

其中 $n$ 表示数组中元素的个数。待比较序列

$x_i=\left(x_i\left(1\right),x_i\left(2\right),\cdots ,x_i\left(n\right)\right)$ (2)

其中 $i$ 表示待比较序列的个数，待比较序列中元素的个数与参考序列中的相同。 $x_i$ 对 $x_0$ 在 $k$ 点的灰色关联系数为

$\xi \left(x_0\left(k\right),x_i\left(k\right)\right)=\frac{{\Delta }_{\min }+\rho {\Delta }_{\max }}{{\Delta }_{0i}\left(k\right)+\rho {\Delta }_{\max }}$ (3)

其中 ${\Delta }_{\min }=\underset{k}{\min }\underset{i}{\min }\left|x_0\left(k\right)-x_i\left(k\right)\right|$ ， ${\Delta }_{\max }=\underset{k}{\max }\underset{i}{\max }\left|x_0\left(k\right)-x_i\left(k\right)\right|$ ， ${\Delta }_{0i}\left(k\right)=\left|x_0\left(k\right)-x_i\left(k\right)\right|$ ； $\rho \in \left(0,1\right]$ 是事先设定的常数，称为分辨率系数，一般情况下均取 $\rho =0.5$ 。灰色关联度为

$\gamma \left(x_0,x_i\right)=\frac{1}{n}{\displaystyle \underset{k=1}{\overset{n}{\sum }}{\xi }_{0i}\left(k\right)}$ (4)

3. 基于GSVM的密写分析方法

3.1. 特征提取

图像进行1层db8小波变换后，利用M. K. Mihcak等 [6] 提出的去噪滤波器可以获得噪声信号。根据文献 [3] ，噪声信号由其概率分布函数(Probability Distribution Function, PDF)唯一确定。将PDF记为 $p$ ，应用指数核 ${\text{e}}^{tx}$ ，并进行Taylor展开，可将 $p$ 映射到一个参数空间，如下式：

$M\left(x\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}p\left(t\right){\text{e}}^{tx}\text{d}t}={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}p\left(t\right)\left(1+tx+\frac{t^2{x}^2}{2!}+\cdots +Q_n\left(t\right)\right)\text{d}t}=1+m_{1}x+\frac{m_2}{2!}{x}^2+\cdots +R_n\left(x\right)$ (5)

上式作为小波域中噪声信号的多项式表示，在统计上，被当作矩生成函数，可通过其系数矩阵求得，其中 $m_i$ 是 $i$ 阶矩， $Q_n$ 和 $R_n$ 随着 $n$ 的增大，趋近于0。所以，可以将矩作为其特征，而又可避免求 $p$ 的复杂性。通过大量的实验，最终，在子带内，选择经二阶矩的标准差 $\sqrt{m_2}$ 标准化后的11个矩作为特征向

量，即 ${m^{\prime }}_i=\frac{m_i}{\sqrt{m_2^i}},i=4,6,\cdots ,24$ (经文献 [6] 中的去噪滤波器所得噪声信号的PDF具有奇偶对称性)，在

$LH,HL,HH$ 三个子带内计算，可得一个33维的特征向量。

3.2. 最优类特征产生

将训练样本中的正类样本(含密图像样本) $T_i\left(i=1,2,\cdots ,n\right)$ 的特征向量，作为GA的初始种群，采用实数编码方式。设样本 $i$ 的代价函数为

${\Psi }_i=1-\frac{1}{n}{\displaystyle \underset{j=1}{\overset{n}{\sum }}\gamma \left(T_i,T_j\right)}$ (6)

其中 $\gamma \left(T_i,T_j\right)$ 表示种群中样本 $i$ 与样本 $j$ 的灰色关联度。 ${\Psi }_i$ 越小，说明样本 $i$ 与种群中的其余样本越相似，越能代表整个种群。所有样本的代价函数值构成种群的代价函数集合 $\Psi =\left\{{\Psi }_1,{\Psi }_2,\cdots ,{\Psi }_n\right\}$ 。采用rank-scale [7] 方法，对集合中的代价函数值按升序排列后，排在第 $j$ 位的样本的适应度为

${\varphi }_j=\frac{n}{\sqrt{j}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{1}{\sqrt{i}}}}$ (7)

利用上式，计算种群中所有样本的适应度。根据适应度进行轮盘赌的适应机制，被选中的个体进行单点交叉和变异的遗传操作，形成中间种群，并将其与父代种群合并，计算合并种群中所有样本的代价函数和适应度，将适应度大的前 $n$ 个样本作为下一代种群，开始下一次的迭代。当种群中含有 ${\Psi }_i$ 小于0.05的样本时，循环结束，此样本的特征向量为最优类特征向量；或者满足别的条件，循环结束时，代价函数最小的样本特征为最优类特征。

3.3. GSVM分类器构造

将上面产生的最优类特征记为 $x_0$ ，则其与训练样本 $i$ 的灰色关联度为 $\gamma \left(x_0,x_i\right)$ ，简记为 ${\gamma }_0\left(x_i\right)$ ，引入 ${\gamma }_0\left(x_i\right)$ 后，训练样本集可表示为：

$\left(x_1,y_1,{\gamma }_0\left(x_1\right)\right),\left(x_2,y_2,{\gamma }_0\left(x_2\right)\right),\cdots ,\left(x_l,y_l,{\gamma }_0\left(x_l\right)\right)$ (8)

其中， $x_j\in R^n$ 为样本的特征向量， $y_j\in \left\{-1,1\right\}$ 为类标识， $0<{\gamma }_0\left(x_j\right)\le 1$ 是样本特征与类特征的灰色关联度， $j=1,\cdots ,l$ ；并设 $\varphi :x\subseteq R^n\to x\subseteq H$ 是从原始特征空间 $R^n$ 到一个高维特征空间 $H$ 的变换。则文献 [8] 中非线性分类问题转化为求解如下以 ${\left(w,b,\epsilon \right)}^{\text{T}}$ 为决策变量的二次规划问题：

$\{\begin{array}{l}\underset{w,b,\epsilon }{\min }\frac{1}{2}{\Vert w\Vert }^2+C\left({\displaystyle \underset{j=1}{\overset{l}{\sum }}{\gamma }_0\left(x_j\right){\epsilon }_j}\right)\\ \text{s}\text{.t}\text{.}{y}_j\left(\left(w^{\text{T}},{\varphi }_j\right)+b\right)+{\epsilon }_j\ge 1,j=1,2,\cdots ,l\\ {\epsilon }_j\ge 0,j=1,2,\cdots ,l\end{array}$ (9)

其中， $C>0$ 是一个自定义的惩罚因子， ${\epsilon }_j$ 是支持向量机目标函数中的分类误差，由(9)式看出：小的 ${\gamma }_0\left(x_j\right)$ 可以减小 ${\epsilon }_j$ 在其中的影响，也可认为相应的 $x_j$ 是不重要的样本。

引入核函数 $K\left(x_j,x_i\right)=\varphi \left(x_j\right)\varphi \left(x_i\right)$ ，则高维空间上的内积运算只需在原空间上进行，(9)式的对偶规划式变为：

$\{\begin{array}{l}\underset{a}{\min }\frac{1}{2}{\displaystyle \underset{j=1}{\overset{l}{\sum }}{\displaystyle \underset{i=1}{\overset{l}{\sum }}{a}_j{a}_{i}K\left(x_j,x_i\right)}}-{\displaystyle \underset{j=1}{\overset{l}{\sum }}{a}_j}\\ \text{s}\text{.t}\text{.}{\displaystyle \underset{j=1}{\overset{l}{\sum }}{a}_j{y}_j=0}\\ 0\le a_j\le {\gamma }_0\left(x_j\right)C,j=1,2,\cdots ,l\end{array}$ (10)

这种将最优类特征与训练样本的灰色关联度 ${\gamma }_0\left(x_j\right)$ 引入到样本中，经训练所得的支持向量分类机称为灰色支持向量分类机。

4. 实验结果分析

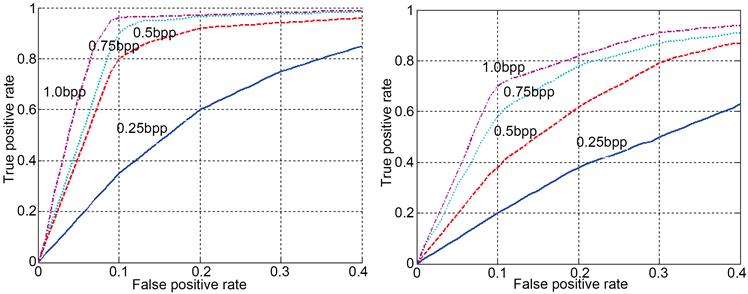
通过对文中所提算法和文献 [3] 中算法的结果进行比较，来分析算法的性能。公平起见，要在相同的条件下进行。所以与文献 [3] 一样，实验图像集也来源于文献 [9] ，由2375幅尺度为1500 × 2100像素、存储格式为TIFF的32位彩色扫描图像组成。同样，也将样本图像转换为灰度图像。嵌入方法是经典的LSB方法，嵌入率分别为0.25 bpp (bits per pixel)，0.5 bpp，0.75 bpp和1.0 bpp。图1(a)和图1(b)分别给出了文中算法和文献 [3] 中算法在上述图像集上的ROC (Receiver Operating Characteristic)分类性能曲线。从图中可以看出，文中所提算法的性能要好于文献 [3] 中算法的性能，即相同正确接受率(True positive rate)下的错误接受率(False positive rate)较小。这是因为在对分类器进行训练时引入了正类样本(含密图像)的最优类特征与训练样本的灰色关联度，减小了负类样本(原始图像)中的离群点，即靠近正类样本的原始图像在支持向量机目标函数中分类误差的影响，所以使得将负类样本当作正类样本的概率减小。

下面从最终的分类结果来衡量文中所提算法的性能。同样是上述的图像集，把这些图像按4:1分成两组并各复制四份，用经典的LSB方法分别以嵌入率为0.25 bpp，0.5 bpp，0.75 bpp和1.0 bpp给四份复

(a)(b)

Figure 1. Steganalysis result of different embedded capacity: (a) experiment result of proposed algorithm; (b) experiment result of Holotyak’s method

图1. 不同嵌入容量的隐写分析实验结果：(a) 文中方法实验结果；(b) Holotyak方法实验结果

Table 1. True positive rate of original images and stegano images

表1. 原始图像和含密图像的正确分类结果

制图像嵌入秘密信息。实验中，用没有嵌入秘密信息的第一组图像和一份经复制并嵌入了秘密信息的第一组图像组成训练样本集来训练上面构造的GSVM，然后用训练好的GSVM对没有嵌入秘密信息的第二组图像和经复制并以相同嵌入率嵌入了秘密信息的第二组图像组成测试集来测试，其余三份嵌入秘密信息的图像也进行相同的运用，共得到四组测试数据。表1给出了上述实验中原始图像和含密图像各自的正确检测率与文献 [3] 中方法正确检测率的对比。从表中同样可以看出，文中所提算法的性能较文献 [3] 中的要好。原因是在对分类器训练时削弱了离群点的作用。

5. 结论

文中提出了一种新的基于GA和GSVM的图像通用密写分析算法。在对SVM训练时，引入了样本与类特征的灰色关联度，构造了GSVM，减小了离群点的作用。另外，在计算灰色关联度时，采用GA来搜索最优类特征作为参考序列，使得计算出的灰色关联度能真正反映出样本与类的关联程度。最后，用训练好的GSVM进行检测。实验结果表明，在相同条件下，文中提出的通用密写分析算法的错误接受率更低，具有更高的正确检测率。但文中仅对Holotyak的噪声特征进行了测试，下一步研究的重点是寻求更好的分类特征，对所构造的GSVM进行训练，形成更有效的通用密写分析算法。