LIBSVM在铅酸蓄电池寿命预测中的应用研究

Application of LIBSVM in Life Prediction of Lead-Acid Battery

摘要: 铅酸蓄电池作为变电站直流电源系统的核心设备，随着投运时间的增长，将会发生内阻增大、容量减小问题，从而导致铅酸蓄电池组的使用寿命减小。因此，研究铅酸蓄电池的寿命预测方法，对于保障变电站的安全稳定运行具有重要作用。在介绍支持向量机的基本原理的基础上，结合铅酸蓄电池的样本数据，通过交叉验证选取LIBSVM回归机最优参数，通过支持向量机回归预测模型建立铅酸蓄电池的寿命预测模型。实验结果表明，基于LIBSVM的铅酸蓄电池寿命预测模型具有较高的预测精度，该方法是切实可行的。

Abstract: As the core of the DC power supply system, the performance of the lead-acid battery is the safe and stable operation of the whole substation. With the use of lead-acid battery pack time increases, the battery’s internal resistance will increase, the battery capacity will be reduced, resulting in lead-acid battery life. Therefore, it is of great significance to study the life prediction of lead-acid battery. Based on the basic principle of support vector machine (SVM) and the sample data of lead-acid battery, the optimal parameters of LIBSVM regression machine are selected by cross validation, and the life prediction model of lead-acid battery is established by support vector machine regression model. The experimental results show that the LIBSVM-based lead-acid battery life prediction model has high prediction accuracy, and the method is feasible.

1. 引言

变电站的自动化、智能化和无人化值守是智能电网建设发展的趋势，因此随着变电站自动化、智能化程度的发展，变电站直流电源系统所承担的角色和作用将越来越重要。变电站直流电源系统的铅酸蓄电池通常与充电机并联运行，共同为继电保护、自动装置、自动化设备、断路器跳合闸等重要的直流负载提供电源 [1] ，因此当站用交流系统由于故障断电导致充电机无法输出直流电源时，铅酸蓄电池组将作为唯一的直流电源将为直流负载提供紧急的备用直流供电。由此可见，准确评估铅酸蓄电池的运行状态，提高蓄电池的运行可靠性，对于确保变电站紧急情况下的安全运行具有重要意义。

铅酸蓄电池组随着运行使用时间的增长，其内阻将会增大，铅酸蓄电池的容量会减小，从而导致铅酸蓄电池的寿命会减少。常规的核对性放电实验是监测铅酸蓄电池剩余容量比较常用和可靠的方法，但是这种方法需要对蓄电池进行充多次重复的充放电实验，不仅试验工作复杂，而且多次放电实验也会加速铅酸蓄电池的老化，影响蓄电池的使用寿命。由于研究发现蓄电池寿命与其端电压、健康状态等因素密切相关，因此，围绕铅酸蓄电池端电压和健康状态两个状态变量开展蓄电池寿命预测的方法研究受到关注。目前，铅酸蓄电池寿命预测方法主要分为两类，即基于经验的方法和基于性能的方法 [2] 。基于经验的方法也叫做基于统计规律的方法，主要分为：老化积累方法 [3] 、安时法、加权安时法 [4] 、循环周期数法。基于电池性能的寿命预测则是在考虑影响电池老化的不同因素基础上，研究用于评估电池性能的模型。依据所考虑影响因素的数据信息来源，主要分为基于数据驱动、基于机理和基于特征三类 [5] 。文献 [6] 针对航空铅酸蓄电池容量预测的复杂性和非线性等问题,提出了一种基于概率神经网络(PNN, probabilistic neural network)的航空铅酸蓄电池容量预测模型。文献 [7] 提出了一个灰色系统预测模型和故障率相结合的混合预测方法，利用故障率函数对系统各个观测时刻的平均剩余寿命进行估计，之后，将系统各个观测时刻的平均剩余寿命看成是灰色动态系统的灰色序列，建立灰色预测模型，对系统之后的退化趋势进行预测，从而得到系统下一观测时刻的剩余寿命。文献 [8] 在现有退化建模方法的基础上，将时变应力对性能退化量的影响引入到退化模型中，解决了时变温度应力下蓄电池循环寿命预测问题。

近年来，支持向量机(Support Vector Machine, SVM)已经成为解决回归预测问题的一个十分有效的机器学习方法，基于统计学习理论的支持向量回归机采用了结构风险最小化原则来代替经验风险最小化，能较好地解决小样本学习的问题；同时还采用核函数思想，把非线性空间的问题转换到线性空间，降低了算法的复杂度，它既考虑了训练样本的拟合性，又考虑了训练样本的复杂性 [9] [10] [11] 。正是因为SVM有较为完备的理论基础和较好的学习性能，在解决有限样本、非线性、高维模式识别和回归问题中表现出许多特有的优势，在分类识别、函数逼近和信息融合等领域得到了成功的应用。

由于通过实际的蓄电池容量检测试验需要高昂的成本，可以通过阀控式铅酸蓄电池的端电压和内阻等信息与其容量之间存在的复杂非线性关系对阀控式铅酸蓄电池的容量进行预测。本文采用LIBSVM的方法建立预测铅酸蓄电池寿命的模型，既考虑了阀控式铅酸蓄电池样本数据的拟合性，又考虑了其样本数据的复杂性和非线性对应关系，通过对铅酸蓄电池的特征向量进行学习训练，经过Grid-Search法交叉验证确定了该回归模型的最优参数组合，仿真结果表明该模型预测精度高，与实际值拟合度良好。

2. SVM基本原理

SVM是在统计学习的基础上发展起来的一种新的机器学习方法，在统计学习理论的VC理论和结构风险最小化原则的基础上，SVM能够根据有限样本信息，在模型的复杂性和学习能力之间寻求最佳折衷，避免了局部极小值点。同时，SVM避免了人工神经网络常常出现的“过学习”问题，具有良好的推广性能和较好的分类精确性，对于有限训练样本得到的决策规则对独立的测试集仍然能够得到小的误差。SVM最初被用于分类问题，后来在函数逼近和回归预测等方面也取得了良好的效果。

当SVM用于回归预测时，称为SVM回归机。通常，SVM将所有样本数据分为两类，一类是训练样本，用来训练得到合适的模型；另一类是测试样本，用来测试训练好的模型的性能。假设一个包含l个样本的训练集： $T=\left\{\left(x_{\text{1}},y_{\text{1}}\right),\left(x_{\text{2}},y_{\text{2}}\right),\cdots ,\left(x_{\text{l}},y_{\text{l}}\right)\right\}\in \left(R^n\times R\right)$ ，其中， $x_i\in R^n$ 表示第i个输入数据， $y_i\in R$ 是第i个输出数据。要求找到一个定义在Rⁿ上的函数f(x)，由它可以对任一输入x去找到与之对应的输出，即y，换句话说也就是要找到一个可表示或反映出y与x之间的关系的函数。

设有一个给定的训练样本集合，它的表示为

$S=\left\{\left(x_i,y_i\right)|x_i\in R^n,y\in R,i=1,2,\cdots ,l\right\}$ (1)

定义1.1：样本S是e-线性近似的，如果存在一个超平面 $f\left(x\right)=\left(w,x\right)+b$ ，其中 $w\in R^n$ ， $b\in R$ ，下面的式子成立：

$\left|y_i-f\left(x_i\right)\right|\le \epsilon ,i=1,2,\cdots ,l$ (2)

用d_i表示点到超平面的距离，则有：

$d_i=\frac{\left|\left(w,x\right)+b-y_i\right|}{\sqrt{1+{\Vert w\Vert }^2}}$ (3)

因为S是e-线性近似的，所以有：

$\left|\left(w,x\right)+b-y_i\right|\le \epsilon ,i=1,2,\cdots ,l$ (4)

这样可以得到：

$d_i=\frac{\left|\left(w,x\right)+b-y_i\right|}{\sqrt{1+{\Vert w\Vert }^2}}\le \frac{\epsilon }{\sqrt{1+{\Vert w\Vert }^2}},i=1,2,\cdots ,l$ (5)

定义1.2：最大化集合S中的点到超平面的距离上界而得到的超平面，称为e-线性近似集S的最优近似超平面。

由上述定义可知通过最大化 $\epsilon /\sqrt{1+{\Vert w\Vert }^2}$ ，或最小化 $\sqrt{1+{\Vert w\Vert }^2}$ 便可得到最优近似超平面。且进一步可说要得到最优近似超平面只需要最小化 ${\Vert w\Vert }^2$ 即可。所以我们可将线性回归问题转化为下面的优化问题：

$\begin{array}{l}\min \frac{1}{2}{\Vert w\Vert }^2\\ \text{s}\text{.t}\text{.}\left|\left(w,x\right)+b-y_i\right|\le \epsilon ,i=1,2,\cdots ,l\end{array}$ (6)

对于这样的一个二次规划问题，相比于直接求法，人们更多选用间接求解，即先将问题转化，找到它的对偶问题，接着再求解即可。要求出原问题的对偶问题，需引入Lagrange函数，表示如下：

$L\left(w,b,a,a^{*}\right)=\frac{1}{2}{\Vert w\Vert }^2-{\displaystyle \underset{i=1}{\overset{l}{\sum }}{a}_i\left(\epsilon -y_i+\left(w,x_i\right)+b\right)}-{\displaystyle \underset{i=1}{\overset{l}{\sum }}{a}_i^{*}\left(\epsilon +y_i-\left(w,x_i\right)-b\right)}$ (7)

式(7)中， $a_i,a_i^{*}\ge 0,i=1,2,\cdots ,l$ 。

Lagrange对偶问题为：

$\underset{a,a*}{\max }\underset{w,b}{\min }L\left(w,b,a,a^{*}\right)$ (8)

根据Kuhn-Tucker条件，函数L的极值应当满足下列条件：

$\frac{\partial L}{\partial w}=0,\frac{\partial L}{\partial b}=0$ (9)

于是得到：

$w={\displaystyle \underset{i=1}{\overset{l}{\sum }}\left(a_i-a_i^{*}\right)x_i}$ (10)

${\displaystyle \underset{i=1}{\overset{l}{\sum }}\left(a_i-a_i^{*}\right)}=0$ (11)

把式(10)和式(11)代入式(7)，得到原优化问题的对偶形式为：

$\begin{array}{l}\underset{a,a*}{\min }\frac{1}{2}{\displaystyle \underset{i=1,j=1}{\overset{l}{\sum }}\left(a_i^{*}-a_i\right)\left(a_j^{*}-a_j\right)\phi \left(x_i-x_j\right)}+\epsilon {\displaystyle \underset{i=1}{\overset{l}{\sum }}\left(a_i^{*}-a_i\right)}-{\displaystyle \underset{i=1}{\overset{l}{\sum }}{y}_i\left(a_i^{*}-a_i\right)}\\ \text{s}\text{.t}\text{.}{\displaystyle \underset{i=1}{\overset{l}{\sum }}\left(a_i^{*}-a_i\right)}=0\\ a_i^{*},a_i\ge 0,i=1,2,\cdots ,l\end{array}$ (12)

因为考虑到误差的可能性，故在此引入两个松弛变量：

${\xi }_i,{\xi }_i^{*}\ge 0,i=1,2,\cdots ,l$ (13)

这时优化方程为：

$\begin{array}{l}\min \frac{1}{2}{\Vert w\Vert }^2+\gamma {\displaystyle \underset{i=1}{\overset{l}{\sum }}\left({\xi }_i+{\xi }_i^{*}\right)}\\ \text{s}\text{.t}\text{.}\left(w,\phi \left(x_i\right)\right)+b-y_i\le {\xi }_i^{*}+\epsilon ,i=1,2,\cdots ,l\\ y_i-\left(w,\phi \left(x_i\right)\right)-b\le {\xi }_i^{*}+\epsilon ,i=1,2,\cdots ,l\\ {\xi }_i,{\xi }_i^{*}\ge 0,i=1,2,,\cdots ,l\end{array}$ (14)

为了对这个二次规划问题进行求解，在此又引入Lagrange函数：

$\begin{array}{c}L\left(w,b,a,a^{*}\right)=\frac{1}{2}{\Vert w\Vert }^2+\gamma {\displaystyle \underset{i=1}{\overset{l}{\sum }}\left({\xi }_i+{\xi }_i^{*}\right)}-{\displaystyle \underset{i=1}{\overset{l}{\sum }}{\eta }_i\left({\xi }_i+{\xi }_i^{*}\right)}\\ -{\displaystyle \underset{i=1}{\overset{l}{\sum }}{a}_i\left({\xi }_i+\epsilon -y_i+\left(w,\phi \left(x_i\right)\right)+b\right)}\\ -{\displaystyle \underset{i=1}{\overset{l}{\sum }}{a}_i^{*}\left({\xi }_i^{*}+\epsilon -y_i-\left(w,\phi \left(x_i\right)\right)-b\right)}\end{array}$ (15)

其中， $a_i,a_i^{*}\ge 0,i=1,2,\cdots ,l$ 。并且函数L的极值满足下列条件：

$\frac{\partial L}{\partial w}=0,\frac{\partial L}{\partial b}=0,\frac{\partial L}{\partial {\xi }_i}=0,\frac{\partial L}{\partial {\xi }_i^{*}}=0$ (16)

于是得到：

$w={\displaystyle \underset{i=1}{\overset{l}{\sum }}\left(a_i-a_i^{*}\right)x_i}$ (17)

${\displaystyle \underset{i=1}{\overset{l}{\sum }}\left(a_i-a_i^{*}\right)}=0$ (18)

$\gamma -a_i-{\eta }_i=0,i=1,2,\cdots ,l$ (19)

$\gamma -a_i^{*}-{\eta }_i^{*}=0,i=1,2,\cdots ,l$ (20)

把式(17)~(20)代入式(15)，得到Lagrange对偶问题为：

$\begin{array}{l}\min \frac{1}{2}{\displaystyle \underset{i=1,j=1}{\overset{l}{\sum }}\left(a_i^{*}-a_i\right)\left(a_j^{*}-a_j\right)\phi \left(x_i-x_j\right)}+\epsilon {\displaystyle \underset{i=1}{\overset{l}{\sum }}\left(a_i^{*}-a_i\right)}-{\displaystyle \underset{i=1}{\overset{l}{\sum }}{y}_i\left(a_i^{*}-a_i\right)}\\ \text{s}\text{.t}.{\displaystyle \underset{i=1}{\overset{l}{\sum }}\left(a_i^{*}-a_i\right)}=0\\ 0\le a_i^{*},a_i\le \gamma ,i=1,2,\cdots ,l\end{array}$ (21)

用支持向量机解决非线性问题时，通常会经过某种变换函数将低维空间的非线性数据变量映射到高维数据空间，然后再对这个高维的特征空间进行线性回归，建立线性模型：

$f\left(x,w\right)=\left(w\cdot \phi \left(x\right)\right)+b$ (22)

而实现这种低维到高维的转换是通过核函数实现的，具体表达式如下：

$k\left(x_i,x_j\right)=\phi \left(x_i\right)\phi \left(x_j\right)$ (23)

式(23)中， $k\left(x_i,x_j\right)$ 为核函数，满足Mercer条件。它接受两个低维空间里的向量，计算出经过某个变换后在高维空间里的向量内积值，这样它就把特征空间的点积运算化成了低维原始空间的核函数运算，巧妙地解决了高维特征空间中计算带来的“维数灾难”。

将式(21)求得的最优解和式(23)代入式(22)得到：

$f\left(x\right)={\displaystyle \underset{i=1}{\overset{l}{\sum }}\left(a_i^{*},a_i\right)K\left(x,x_i\right)}+b$ (24)

3. 实验过程

3.1. 问题分析

铅酸蓄电池性能的降低或劣化主要由以下几个原因导致：1) 外观上，铅酸蓄电池极柱出现腐蚀或突出现象、外壳变形、安全阀周围有酸雾溢出等均可体现出铅酸蓄电池的性能降低；2) 铅酸蓄电池的工作温度升高，测量工作温度以现在的维护水平大多只可测量铅酸蓄电池外壳的温度；3) 铅酸蓄电池性能降低主要体现在内在参数的异常：内阻值偏大、容量降低。铅酸蓄电池性能的降低会使得其寿命减少，铅酸蓄电池的寿命通常包括存储寿命(电池失效前在不工作状态下的存储时间)、使用寿命(电池失效前反复多次充放电所累积的总的可放电时间)和循环寿命(电池失效前可反复充放电的次数总和)。其中，使用最为广泛的是循环寿命 [12] 。

判断一个铅酸蓄电池是否有效，一般采用以下两种方法进行检测：1) 铅酸蓄电池容量检测：这是根据基本的理论来检测的方法，能判断铅酸蓄电池在其寿命周期里的位置，所以是最理想的方法。按此方法检测出的铅酸蓄电池电池容量是最直接、最准确的，但是进行测试所需的费用十分昂贵。2) 铅酸蓄电池内部欧姆电阻检测：通过测量电池的内阻来确定电池的性能，被验证是非常有效的方法，并且也可以作为容量测试的一种替代手段。内阻作为铅酸蓄电池性能体现的重要指示参数，虽然它和容量检测相比，还无法100%的判定阀控式铅酸蓄电池状态，但实践经验证明它能够检测出95%以上有问题的电池 [13] 。

通常情况下，铅酸蓄电池失效的主要原因是容量衰减，因此可以认为预测蓄电池寿命与预测蓄电池的剩余容量是等价的，即铅酸蓄电池的剩余容量达到失效值时所对应的充放电次数即为蓄电池的循环寿命 [14] 。蓄电池的剩余容量和蓄电池内的很多因素有关，其中主要影响因素是铅酸蓄电池的端电压和健康状态(State of Health, SOH)，电池的SOH是指电池目前所能释放的最大容量和电池全新时能释放的最大容量的比值 [15] 。

3.2. 建立铅酸蓄电池的寿命预测模型

以铅酸蓄电池的SOH和端电压(U/V)为输入量，电池的剩余容量(q/Ah)为输出量，采用LIBSVM-mat- 2.89工具箱建立数学模型，核函数选择径向基核函数 [16] ，模型的主要参数是错误惩罚因子C和核函数中的Grammar函数的参数g，可以通过Grid-Search法找出一组最佳参数(C,g) [17] [18] 。本文以表1中样本数据中的1~20组数据作为训练样本，得到合适的预测模型，然后以表1中样本数据的20~30组数据作为测试样本，以测试样本数据的均方误差(Mean Square Error, MSE)来测试训练模型的性能好坏。

试验的基本步骤如下：

1) 对初始数据进行归一化处理，将数据缩放到[0,1]之间，避免特征值的范围过大或过小，从而对试验结果产生影响。

2) 选择SVM的类型为e-SVR，核函数为RBF函数，设置e-SVR中损失函数p的值为0.01。

3) 以预测数据的均方误差为性能指标，采用Grid-Search法找一组最佳的参数(C,g)，使得预测样本的MSE最小。

4) 将得到的最佳参数(C,g)代入LIBSVM算法中进行训练，得到训练好的模型。

5) 将训练好的模型输入LIBSVM的预测函数中，得到测试样本的预测值。

6) 将测试样本的预测值反归一化，画图对比分析测试样本的真实值和预测值。

3.3. 实验结果与分析

仿真实验结果如图1和图2所示。图1是通过Grid-Search法寻找最佳参数(C,g)的寻优结果图，最终找到的最佳参数为C = 95.8，g = 2.3。图2是在最优参数的条件下，即s = 3，C = 95.8，g = 2.3，p = 0.01，v = 5时，进行预测得到的测试样本的预测值和真实值的对比图，图中横坐标表示表1中30组样本数据中的第21~30组样本数据的编号，纵坐标表示样本数据剩余容量的真实值和预测值。由图2可以看出，预测结果十分接近测试样本的真实值，预测效果良好。预测结果为：MSE= 0.00334199，R= 0.98072，R

Table 1. Sample data of lead-acid batteries

表1. 铅酸蓄电池的样本数据

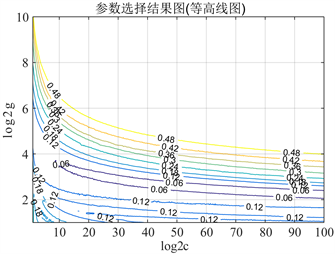
Figure 1. Optimization of model parameters

图1. 模型参数的寻优结果

Figure 2. Forecast result of the test samples

图2. 测试样本的预测结果

为平方相关系数。从均方误差来看，LIBSVM建立的铅酸蓄电池寿命预测模型具有很高的预测精度，从平方系数R来看，预测结果与实际值拟合效果很好，并且能够较好地反映数据变化的趋势。

4. 结论

本文针对变电站直流电源系统的铅酸蓄电池的寿命预测问题，采用实际铅酸蓄电池的样本数据，结合LIBSVM来预测铅酸蓄电池的寿命，通过Grid-Search法搜寻最优参数：错误惩罚因子C和核函数参数g。预测结果表明LIBSVM预测到的铅酸蓄电池的寿命与测试样本的真实值十分接近，回归拟合效果很好，验证了该模型的准确性和可行性。