基于TEC曲线拟合的DS/FH跳扩频跟踪技术

Carrier Tacking Technology in DS/FH Spread Spectrum Based on TEC Curve Fitting

摘要: 针对DS/FH跳扩频系统中，不同跳频点在空间信道传输的相移不一致，引起的接收信号相位不连续这一问题，在分析信道传输特性的基础上，根据跳扩频接收信号的特点，提出了一种基于TEC曲线拟合的跳扩频跟踪方法，将电离层非线性相位偏移补偿引入跟踪环路，有效地解决了相位跳变导致的环路失锁的问题，提高了跟踪精度。最后用MATLAB模拟一组仿真数据，用本文所提的方法对电离层相位偏移进行估计，相位估计误差在±10°以内，可以满足跟踪环路的要求。

Abstract: In DS/FH spread spectrum system, different hopping frequency has different phase shift, which leads to the discontinuous phase of the receiving signal. On the basis of analysis of channels’ transfer characteristics, a carrier tacking technology based on TEC curve fitting is proposed which uses the character of the DS/FH receiving signal. The ionosphere phase compensation is imported in the tracking loops, which solves the problem of loop locking caused by the phase hopping. In addition, tacking accuracy is improved. Finally, MATLAB is used to estimate the ionosphere phase compensation by the method proposed in this paper. The simulation results show that, the phase estimation error is within plus or minus 10, which meets the tracking loop requirements.

1. 引言

DS/FH (Direct Sequence & Frequency Hopping)是一种既具有直接序列扩频信号的隐蔽性，又具有跳频信号抗干扰性能的混合扩频系统，是国内外公认的最有效的抗干扰、抗截获的测控体制 [1] [2] [3] 。近些年来，已成为国内外新型抗干扰测控系统的研究热点。

地球的电离层是一个部分电离的等离子体。电离层给无线电波带来五种效应：多普勒频移、信号衰减、信号弯曲、极化角旋转和频率相关的色散效应。DS/FH混合扩频系统中，发射信号是由频率不同、相位连续的单载波构成的，由于电离层的色散效应，不同跳频点在空间信道传输的相移不一致，导致接收机接收到的DS/FH混合扩频信号相位不连续，无法通过现有的标校手段获知，从而导致无法对载波进行相位跟踪，也不能对数据进行相干解调 [4] [5] ，也就是说，如何对空间信道的相移特性进行在线实时估计，是提高混合跳扩频体制信号跟踪灵敏度的关键技术难题。

目前，针对DS/FH系统中空间信号相移特性的实时估计问题，相关的论文鲜见报道，提高跟踪精度又是影响测距精度的关键技术要求。因此，迫切需要对该问题进行研究。本文提出了基于TEC(电离层电子浓度总含量)曲线拟合的载波跟踪技术，通过对空间信道相移特性建模、估计，消除相位不连续，提高载波跟踪精度。

电离层相位污染抑制可广泛应用于各种谱估计、时频分析、参数估计方法的信号处理领域。例如在天波超视距雷达(OTHR)体制中，电离层相位污染引起OTHR杂波频谱展宽，严重制约低速目标检测。高频天波海态雷达利用电离层折射实现超远距离、大范围海态监测，电离层是天波海态雷达的重要传输媒质，电离层的非平稳性引起高频天波海态雷达回波信号的相位路径扰动。本文提出的利用瞬时频率和相位的关系来估计电离层相位曲线的方法，同样适用于诸如OTHR等系统中，作为电离层相位污染的抑制措施。

2. 传输信道特性分析

文献 [6] 中阐述了电离层效应对GPS(全球定位系统)信号捕获及跟踪的影响。电磁波通过电离层会产生附加时延 $\tau =-\frac{40.28}{c{f}^2}\cdot TEC$ [7] [8] ，附加相移可以表示为 $\varphi =-2\text{π}f\tau =\frac{2\text{π}\times 40.28}{cf}\cdot TEC$ 。其中， $TEC$ 为传播路径上的电子总数，单位为TECU，以e/m²为单位表示，通常取10¹⁶。 $TEC$ 随一天的时间、卫星仰角、用户位置、季节、电离通量、磁活动性、日斑周期等变化而变化，可改变1到2个数量级 [9] [10] 。因此，空间信道的变化规律无法预知，也无法预先补偿。

$\varphi$ 按泰勒级数在 $f_0$ 处展开，即

$\varphi ={\varphi |}_{f=f_0}+(f-f_0)\cdot {{\varphi }^{\prime }|}_{f=f_0}+\frac{{\left(f-f_0\right)}^2}{2!}\cdot {{\varphi }^{″}|}_{f=f_0}+\cdots$ (1)

泰勒展开的第一项即常数项，第二项即一次项表示相位频移的线性部分，相移 $\varphi$ 减去线性部分，可得

${\varphi }_{非线性}=\frac{2\text{π}\times 40.28}{cf}\cdot TEC-\frac{2\text{π}\times 40.28}{c{f}_0}\cdot TEC-\left(f-f_0\right)\cdot \frac{2\text{π}\times 40.28}{c{f}_0{}^2}\cdot TEC$ (2)

相移的线性部分对应群时延是常数的部分，此时信号的不同频率分量具有相同的群时延，信号没有畸变。

不同 $TEC$ 下，不同频率的相位响应如图1所示。减去线性部分后相位非线性响应如图2所示。

电离层和信道响应可以近似用一个二次函数来表示，即 ${\varphi }_{非线性}=A+B\cdot f+C\cdot f^2$ ，输入为频率，输出为非线性相位响应。

跳频周期内的直扩码是固定的，即跳频码和直扩码是一一对应的，伪码同步以后，跳频码也就同步了，这种同步方法下，跳频码不需要单独跟踪，载波频率不连续点可以被准确锁定。如果能准确锁定相位不连续点的相位偏移，就可以仿照接收信号的不连续性进行相位补偿，从而使载波剥离后可以进行多个跳频信号的相干累积，改善累积后的信噪比，提高载波跟踪精度。

3. TEC曲线拟合方法

在跳扩频系统中，受不同TEC的影响，不同跳频点在空间传输中引入的非线性相移失真无法预测，也不能事先补偿，但从图2的仿真可以看出，虽然电离层电子浓度未知，但对于同一时刻，TEC可视为常数，可以用一个二次函数来拟合。通过对电离层和收发设备对同一电离层浓度下，不同频点的相位影响进行建模，估计出参数就可以进行有效的相位补偿。

对于单个正弦信号 $\exp \left(j2\text{π}\cdot fd\cdot t+j{\varphi }_0\right)$ 来说，当信号频率 $fd$ 远小于采样率 $F_s$ 时，积分后信号相位可以表示为 [11]

${\varphi }_{\Sigma }=2\text{π}fd\cdot \frac{T}{2}+{\varphi }_0$ (3)

其中 $T$ 表示积分时间。

Figure 1. Phase response of different TECU

图1. 不同TECU条件下相位响应

Figure 2. Nonlinear phase response of different TECU

图2. 不同TECU条件下非线性相位响应

用 $\Delta f{d}_0$ 表示捕获阶段确定的载波多普勒值，根据捕获指标要求，去掉部分载波多普勒 $\Delta f{d}_0$ 后残余的多普勒一般很小，可以满足远小于采样率 $F_s$ 的要求。如图3所示，对下变频后接收信号进行积分，积分时间 $T$ 为半个跳频间隔。从图2可以看出，每条非线性相位响应曲线都经过 $\left(f_0,0\right)$ 点，当B，C的估计值得到后，可以算出 $A=-B\ast f_0-C\ast f_0^2$ 。在每个跳频周期内，跳频频点是变化的，速度 $v$ 保持不变。根据速度与多普勒之间的关系 $fd=\frac{v}{c}\cdot f$ ，积分后相位表示为式(4)，用 $noise$ 表示信道及空间传输噪声。

Figure 3. Schematic diagram of phase integral

图3. 相位积分示意图

采用速度和参数联合估计，用矢量参量 $W={\left[vBC\right]}^{\text{T}}$ 表示待估计的3个参量，得到 $W$ 的 $L$ 次观测为

$d=X\cdot W+\epsilon$ (5)

其中

$d=\left[\begin{array}{c}{\varphi }_2-{\varphi }_1+2\text{π}\cdot \Delta f{d}_0\cdot T\\ {\varphi }_3-{\varphi }_2-2\text{π}\cdot \Delta f{d}_0\cdot T\\ ⋮\\ {\varphi }_{2*L}-{\varphi }_{2*L-1}+2\text{π}\cdot \Delta f{d}_0\cdot T\end{array}\right]$ 是已知的观测向量，

$X=\left[\begin{array}{ccc}2\text{π}\frac{1}{c}\cdot f_1\cdot T& \left(f_1-f_0\right)& \left(f_1^2-f_0^2\right)\\ 2\text{π}\frac{1}{c}\cdot \left(f_2\cdot \frac{T}{2}-f_1\cdot \frac{3T}{2}\right)& \left(f_1-f_0\right)& \left(f_1^2-f_0^2\right)\\ ⋮& ⋮& ⋮\\ 2\text{π}\frac{1}{c}\cdot f_L\cdot T& \left(f_L-f_0\right)& \left(f_L^2-f_0^2\right)\end{array}\right]$ 是已知的数据矩阵，

$\epsilon ={\left[{\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_{2*L-1}\right]}^{\text{T}}$ 是误差向量，包括噪声和模型误差两部分。考察误差的平方和：

$r\left(\epsilon \right)={\displaystyle \underset{i=1}{\overset{2*L-1}{\sum }}{\epsilon }_i^2}={\epsilon }^{\text{T}}\epsilon ={\left(d-X\stackrel{⌢}{W}\right)}^{\text{T}}\left(d-X\stackrel{⌢}{W}\right)$ (6)

使误差平方和最小的估计向量 $\stackrel{⌢}{W}$ 称为 $d=X\cdot W+\epsilon$ 的最小二乘解 [12] [13] ：

${\stackrel{⌢}{W}}_{ls}={\left(X^{\text{T}}X\right)}^{-1}{X}^{\text{T}}d$ (7)

跳扩系统中，观测对象可以不断的提供新的输入数据，采用递推算法，可以避免观测矩阵求逆，从而减少计算量以加快估计速度。

4. 载波相位跟踪

在跳频图案已知的情况下 [14] [15] [16] ，由速度的估计结果，根据速度与多普勒之间的关系 $fd=\frac{v}{c}\cdot f$ ，

可以很容易算得多普勒频率，所以对速度的跟踪过程即相当于对频率的跟踪。速度估计值可以用作锁相环的频率牵引，能更快的将信号牵入到稳定跟踪状态。在参数估计的过程中，得到速度和TEC曲线参数的估计值。值得注意的是，在上述估计过程中，假设速度是恒定不变的，这个假设引入的误差可以由锁相环消除。基于TEC曲线拟合的载波跟踪流程如图4所示。

5. 仿真分析

用MATLAB仿真分析本文提出的TEC拟合方法，对DS/FH系统中非线性相位偏移曲线的估计精度。设定跳扩频系统信号的信噪比为48 dB，没有误差的情况下，非线性相位响应即为图2所示曲线，TEC分别取50TECU，100TECU，200TECU，300TECU，400TECU，500TECU，迭代1000次，估计曲线与真实的非线性相位响应曲线对比如图5所示。

图4. 载波跟踪流程图

Figure 4. Flow chart of carrier tracking

图4. 载波跟踪流程图

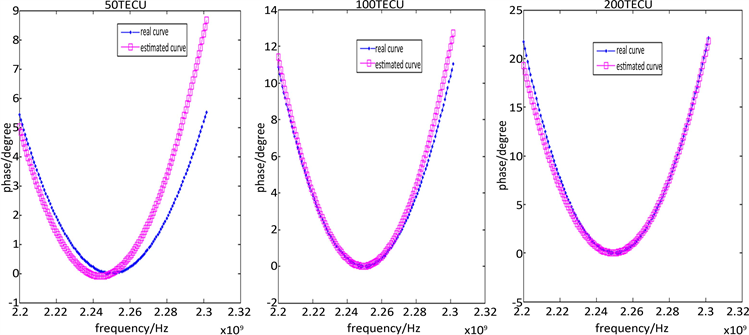(a) TEC = 50 (b) TEC = 100 (c) TEC = 200(a) TEC = 300 (b) TEC = 400(c) TEC = 500

Figure 5. Accuracy analysis of TEC curve fitting methods

图5. TEC曲线拟合方法精度分析

Table 1. Error of the estimated value and true value under different frequency

表1. 不同频点的非线性相位响应估计值与真实值误差

图5所示的仿真结果，非线性相位响应的估计值与真实值的误差，如表1所示。

从表1的分析结果可以看出，本文提出的TEC曲线拟合方法对电离层相位偏移的估计误差在±10˚以内，由式(6)可以看出，误差与TEC参数取值没有必然联系，经过本文所提算法可将误差限制在可接受范围内，这个误差可以用锁相环消除。

6. 结论

DS/FH混合扩频系统的跟踪难度来源于电离层效应，电离层对不同频率的信号引入了不同的非线性相位偏移，较大的相位偏移将导致环路失锁。本文根据DS/FH系统特点，提出的基于TEC曲线拟合的跟踪方法，将电离层非线性相位偏移补偿引入跟踪环路，有效的解决了相位跳变导致的环路失锁的问题，提高了跟踪精度。通过仿真分析证明了该方法的有效性。